LQR for Set-Point Regulation
Linear Quadratic Regulator (LQR) for set-point regulation extends the basic LQR framework to track constant reference signals. This document presents the complete formulation using state augmentation and demonstrates practical implementation.
Problem Overview
Standard LQR vs. Set-Point Regulation
Standard LQR: Drives system states to zero
Set-Point Regulation: Drives system states to constant reference values
This extension is crucial for practical applications where the desired operating point is not the origin.
Problem Formulation
Original System
Consider a discrete-time linear system:
Where:
- : system state
- : control input
- : state transition matrix
- : input matrix
Reference Signal
The constant reference signal evolves as:
Where (identity matrix) for constant references.
State Augmentation
To handle the reference tracking, we augment the state vector:
The augmented system becomes:
Where:
- Transforms tracking problem into regulation problem
- Maintains linear structure for LQR framework
- Enables optimal control for reference following
Tracking Error Definition
The tracking error is defined as:
In terms of the augmented state:
Where is the error extraction matrix.
Cost Function Formulation
Quadratic Performance Function
The objective is to minimize:
Where:
Transformation to Augmented State
Substituting the error definition:
Simplifying:
Augmented Weight Matrices
Define the augmented weight matrices:
The cost function becomes:
The optimal control regulates the tracking error , not the augmented state directly. The augmentation is a mathematical tool to enable LQR application.
LQR Solution
Optimal Control Law
Using the standard LQR framework for the augmented system:
Feedback Gain
The optimal feedback gain is:
Cost-to-Go Matrix
The optimal cost-to-go:
Where the cost-to-go matrix evolves according to:
Algorithm Summary
Backward Recursion:
- Initialize:
- For :
- Compute gain:
- Update matrix:
Forward Implementation:
- For :
- Apply control:
- Update state:
Practical Examples
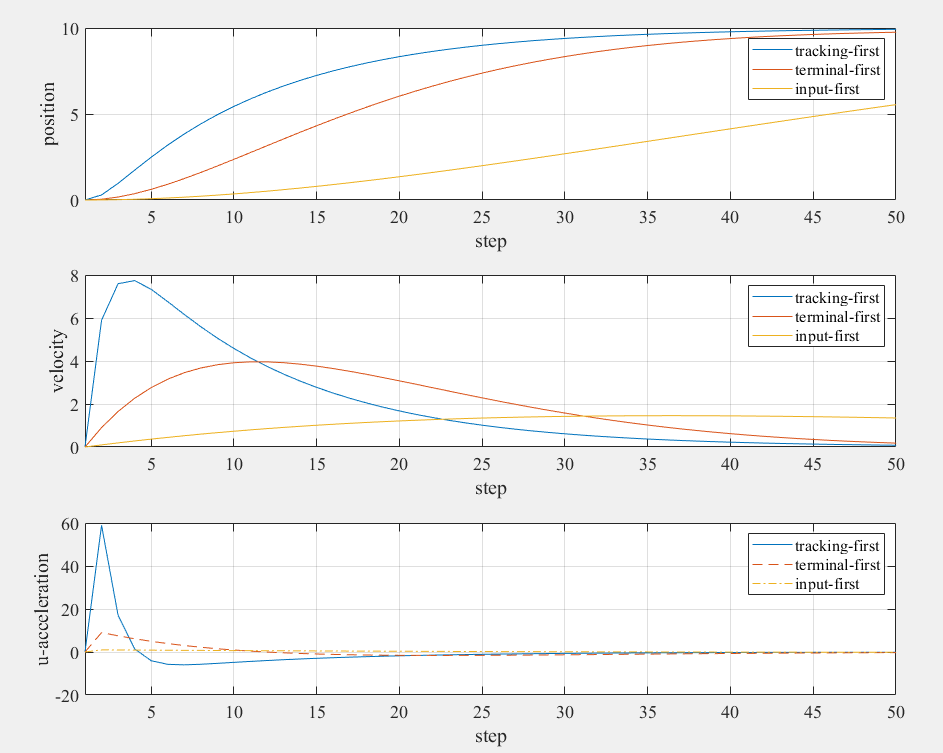
Test Case 1: Double Integrator System
Consider a second-order system (double integrator):
Reference signal:
Objective: Drive the position to 10 and velocity to 0.
Weight Matrix Configurations
We compare three different weight matrix strategies:
Configuration 1: Tracking-First
Weight matrices:
Characteristics:
- High penalty on tracking error during trajectory
- Fast convergence to reference
- Higher control effort
Configuration 2: Terminal-First
Weight matrices:
Characteristics:
- High penalty on final tracking error
- Emphasis on terminal accuracy
- More flexible trajectory
Configuration 3: Input-First
Weight matrices:
Characteristics:
- High penalty on control effort
- Conservative control action
- Slower but energy-efficient response
MATLAB Implementation
%% LQR for Set-Point Regulation
%-----------------------------------------------%
% Youkoutaku: https://youkoutaku.github.io/
% Date: 2024/10/04
% Description: LQR for regulator problem with constant reference signal
%-----------------------------------------------%
clear; close all; clc;
set(0, 'DefaultAxesFontName', 'Times New Roman')
set(0, 'DefaultAxesFontSize', 14)
%% System Model
A = [0 1; 0 0];
n = size(A, 1);
B = [0; 1];
p = size(B, 2);
C = [1 0; 0 1];
D = [0; 0];
%% System Discretization
Ts = 0.1; % Sample time
sys_d = c2d(ss(A, B, C, D), Ts);
A = sys_d.a; % Discretized system matrix A
B = sys_d.b; % Discretized input matrix B
%% Weight Matrices
% Tracking-first LQR
Q1 = [100 0; 0 100]; % Tracking error weight
S1 = [1 0; 0 1]; % Terminal weight
R1 = 1; % Input weight
% Terminal-first LQR
Q2 = [1 0; 0 1]; % Tracking error weight
S2 = [100 0; 0 100]; % Terminal weight
R2 = 1; % Input weight
% Input-first LQR
Q3 = [1 0; 0 1]; % Tracking error weight
S3 = [1 0; 0 1]; % Terminal weight
R3 = 100; % Input weight
%% Initial Conditions
x0 = [0; 0];
x1 = x0; x2 = x0; x3 = x0;
u1 = 0; u2 = 0; u3 = 0;
%% Reference Signal
xr = [10; 2];
Ar = eye(n); % Augmented matrix for constant reference
% Initialize augmented states
z1 = [x1; xr];
z2 = [x2; xr];
z3 = [x3; xr];
%% Augmented System Matrices
Cz = [eye(n) -eye(n)]; % Error extraction matrix
Az = [A zeros(n); zeros(n) Ar]; % Augmented state matrix
Bz = [B; zeros(n, p)]; % Augmented input matrix
% Augmented weight matrices
Sz1 = Cz' * S1 * Cz;
Qz1 = Cz' * Q1 * Cz;
Sz2 = Cz' * S2 * Cz;
Qz2 = Cz' * Q2 * Cz;
Sz3 = Cz' * S3 * Cz;
Qz3 = Cz' * Q3 * Cz;
%% LQR Gain Computation
[F1] = LQR_DP(Az, Bz, Qz1, R1, Sz1);
[F2] = LQR_DP(Az, Bz, Qz2, R2, Sz2);
[F3] = LQR_DP(Az, Bz, Qz3, R3, Sz3);
%% Simulation
k_steps = 50;
x_h1 = zeros(n, k_steps + 1);
x_h2 = zeros(n, k_steps + 1);
x_h3 = zeros(n, k_steps + 1);
x_h1(:, 1) = x1;
x_h2(:, 1) = x2;
x_h3(:, 1) = x3;
u_h1 = zeros(p, k_steps + 1);
u_h2 = zeros(p, k_steps + 1);
u_h3 = zeros(p, k_steps + 1);
for k = 1:k_steps
% Compute control inputs
u1 = -F1 * z1;
u2 = -F2 * z2;
u3 = -F3 * z3;
% Update systems
x1 = A * x1 + B * u1;
x2 = A * x2 + B * u2;
x3 = A * x3 + B * u3;
% Store results
x_h1(:, k + 1) = x1;
x_h2(:, k + 1) = x2;
x_h3(:, k + 1) = x3;
u_h1(:, k + 1) = u1;
u_h2(:, k + 1) = u2;
u_h3(:, k + 1) = u3;
% Update augmented states
z1 = [x1; xr];
z2 = [x2; xr];
z3 = [x3; xr];
end
%% Plotting
figure('Position', [100, 100, 800, 600]);
% Position response
subplot(3, 1, 1);
plot(0:k_steps, x_h1(1, :), 'b-', 'LineWidth', 2);
hold on;
plot(0:k_steps, x_h2(1, :), 'r--', 'LineWidth', 2);
plot(0:k_steps, x_h3(1, :), 'g-.', 'LineWidth', 2);
plot(0:k_steps, xr(1) * ones(1, k_steps + 1), 'k:', 'LineWidth', 1.5);
legend('Tracking-first', 'Terminal-first', 'Input-first', 'Reference', ...
'Location', 'best');
xlim([0, k_steps]);
xlabel('Time step');
ylabel('Position x_1');
title('Position Response');
grid on;
% Velocity response
subplot(3, 1, 2);
plot(0:k_steps, x_h1(2, :), 'b-', 'LineWidth', 2);
hold on;
plot(0:k_steps, x_h2(2, :), 'r--', 'LineWidth', 2);
plot(0:k_steps, x_h3(2, :), 'g-.', 'LineWidth', 2);
plot(0:k_steps, xr(2) * ones(1, k_steps + 1), 'k:', 'LineWidth', 1.5);
legend('Tracking-first', 'Terminal-first', 'Input-first', 'Reference', ...
'Location', 'best');
xlim([0, k_steps]);
xlabel('Time step');
ylabel('Velocity x_2');
title('Velocity Response');
grid on;
% Control input
subplot(3, 1, 3);
plot(0:k_steps, u_h1(1, :), 'b-', 'LineWidth', 2);
hold on;
plot(0:k_steps, u_h2(1, :), 'r--', 'LineWidth', 2);
plot(0:k_steps, u_h3(1, :), 'g-.', 'LineWidth', 2);
legend('Tracking-first', 'Terminal-first', 'Input-first', ...
'Location', 'best');
xlim([0, k_steps]);
xlabel('Time step');
ylabel('Control Input u');
title('Control Effort');
grid on;
sgtitle('LQR Set-Point Regulation Comparison', 'FontSize', 16, 'FontWeight', 'bold');
function [F] = LQR_DP(A, B, Q, R, S)
% LQR solution using dynamic programming
P0 = S;
max_iter = 200;
tolerance = 1e-6;
P_k_minus_1 = P0;
F_prev = inf;
for k = 1:max_iter
F_current = (R + B' * P_k_minus_1 * B) \ (B' * P_k_minus_1 * A);
P_k = (A - B * F_current)' * P_k_minus_1 * (A - B * F_current) + ...
F_current' * R * F_current + Q;
if max(abs(F_current - F_prev), [], 'all') < tolerance
fprintf('LQR converged in %d iterations\n', k);
F = F_current;
return;
end
P_k_minus_1 = P_k;
F_prev = F_current;
end
error('LQR did not converge');
end
Python Implementation
import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import solve_discrete_are
def lqr_regulator(A, B, Q, R, S, x_ref, x0, k_steps):
"""
LQR for set-point regulation
"""
n = A.shape[0]
p = B.shape[1]
# Augmented system matrices
Ar = np.eye(n) # Reference dynamics (constant)
Az = np.block([[A, np.zeros((n, n))],
[np.zeros((n, n)), Ar]])
Bz = np.block([[B],
[np.zeros((n, p))]])
# Error extraction matrix
Cz = np.block([np.eye(n), -np.eye(n)])
# Augmented weight matrices
Sz = Cz.T @ S @ Cz
Qz = Cz.T @ Q @ Cz
# Solve discrete-time Riccati equation
P = solve_discrete_are(Az, Bz, Qz, R, s=Sz)
F = np.linalg.solve(R + Bz.T @ P @ Bz, Bz.T @ P @ Az)
# Simulation
x_traj = np.zeros((n, k_steps + 1))
u_traj = np.zeros((p, k_steps + 1))
x_traj[:, 0] = x0
x = x0.copy()
for k in range(k_steps):
# Augmented state
z = np.concatenate([x, x_ref])
# Control input
u = -F @ z
u_traj[:, k] = u
# Update state
x = A @ x + B @ u
x_traj[:, k + 1] = x
return x_traj, u_traj, F
# System matrices
A = np.array([[0, 1], [0, 0]])
B = np.array([[0], [1]])
# Discretize system (assuming Ts = 0.1)
from scipy.signal import cont2discrete
Ts = 0.1
A_d, B_d, _, _, _ = cont2discrete((A, B, np.eye(2), np.zeros((2, 1))), Ts)
# Weight matrices for different strategies
Q1 = np.array([[100, 0], [0, 100]]) # Tracking-first
S1 = np.array([[1, 0], [0, 1]])
R1 = np.array([[1]])
Q2 = np.array([[1, 0], [0, 1]]) # Terminal-first
S2 = np.array([[100, 0], [0, 100]])
R2 = np.array([[1]])
Q3 = np.array([[1, 0], [0, 1]]) # Input-first
S3 = np.array([[1, 0], [0, 1]])
R3 = np.array([[100]])
# Initial condition and reference
x0 = np.array([0, 0])
x_ref = np.array([10, 2])
k_steps = 50
# Simulate all cases
x1_traj, u1_traj, F1 = lqr_regulator(A_d, B_d, Q1, R1, S1, x_ref, x0, k_steps)
x2_traj, u2_traj, F2 = lqr_regulator(A_d, B_d, Q2, R2, S2, x_ref, x0, k_steps)
x3_traj, u3_traj, F3 = lqr_regulator(A_d, B_d, Q3, R3, S3, x_ref, x0, k_steps)
# Plotting
fig, (ax1, ax2, ax3) = plt.subplots(3, 1, figsize=(10, 8))
time_steps = np.arange(k_steps + 1)
# Position
ax1.plot(time_steps, x1_traj[0, :], 'b-', linewidth=2, label='Tracking-first')
ax1.plot(time_steps, x2_traj[0, :], 'r--', linewidth=2, label='Terminal-first')
ax1.plot(time_steps, x3_traj[0, :], 'g-.', linewidth=2, label='Input-first')
ax1.axhline(y=x_ref[0], color='k', linestyle=':', linewidth=1.5, label='Reference')
ax1.set_xlabel('Time step')
ax1.set_ylabel('Position $x_1$')
ax1.set_title('Position Response')
ax1.legend()
ax1.grid(True)
# Velocity
ax2.plot(time_steps, x1_traj[1, :], 'b-', linewidth=2, label='Tracking-first')
ax2.plot(time_steps, x2_traj[1, :], 'r--', linewidth=2, label='Terminal-first')
ax2.plot(time_steps, x3_traj[1, :], 'g-.', linewidth=2, label='Input-first')
ax2.axhline(y=x_ref[1], color='k', linestyle=':', linewidth=1.5, label='Reference')
ax2.set_xlabel('Time step')
ax2.set_ylabel('Velocity $x_2$')
ax2.set_title('Velocity Response')
ax2.legend()
ax2.grid(True)
# Control input
ax3.plot(time_steps[:-1], u1_traj[0, :-1], 'b-', linewidth=2, label='Tracking-first')
ax3.plot(time_steps[:-1], u2_traj[0, :-1], 'r--', linewidth=2, label='Terminal-first')
ax3.plot(time_steps[:-1], u3_traj[0, :-1], 'g-.', linewidth=2, label='Input-first')
ax3.set_xlabel('Time step')
ax3.set_ylabel('Control Input $u$')
ax3.set_title('Control Effort')
ax3.legend()
ax3.grid(True)
plt.tight_layout()
plt.suptitle('LQR Set-Point Regulation Comparison', fontsize=16, fontweight='bold', y=0.98)
plt.show()
# Print feedback gains
print("Feedback gains:")
print(f"Tracking-first: F1 = {F1}")
print(f"Terminal-first: F2 = {F2}")
print(f"Input-first: F3 = {F3}")
Analysis of Results
Performance Comparison
Based on the simulation results:
Tracking-First Strategy:
- Fastest convergence to reference values
- Higher control effort initially
- Excellent tracking throughout the trajectory
- Best for applications requiring tight tracking
Terminal-First Strategy:
- Balanced approach with moderate control effort
- Good final accuracy with flexible trajectory
- Smooth convergence without excessive overshoot
- Suitable for general regulation tasks
Input-First Strategy:
- Minimal control effort and energy consumption
- Slower convergence but very smooth response
- Conservative approach avoiding aggressive control
- Ideal for systems with actuator limitations
Design Trade-offs
| Strategy | Convergence Speed | Control Effort | Energy Efficiency | Robustness |
|---|---|---|---|---|
| Tracking-first | Fast | High | Low | Medium |
| Terminal-first | Medium | Medium | Medium | High |
| Input-first | Slow | Low | High | High |
Applications and Extensions
1. Multi-Reference Tracking
For time-varying references, the augmentation approach can be extended:
Where represents reference dynamics inputs.
2. Integral Action
Add integral states to eliminate steady-state errors:
3. Output Regulation
For output tracking problems:
Modify the error definition to .
4. Disturbance Rejection
Include disturbance models in the augmentation:
Design Guidelines
Weight Matrix Selection
For tight tracking:
- Use large values
- Moderate values
- Accept higher control effort
For energy efficiency:
- Use large values
- Moderate values
- Accept slower response
For balanced performance:
- Use moderate and values
- Emphasize terminal accuracy with larger
Practical Considerations
- Actuator constraints: Choose to prevent saturation
- Model uncertainties: Use conservative designs
- Noise sensitivity: Balance performance vs. robustness
- Computational limits: Consider real-time implementation requirements
Summary
The LQR set-point regulation framework provides:
- Systematic approach to reference tracking problems
- Optimal control subject to quadratic cost
- Flexible tuning through weight matrix design
- Practical implementation for real systems
The state augmentation technique transforms tracking problems into regulation problems, enabling the application of standard LQR theory to achieve optimal reference following.
References
- Chris Mavrogiannis - LQR Tracking
- Wang, T. (2023). 控制之美 (卷2). Tsinghua University Press.
- Anderson, B. D. O., & Moore, J. B. (2007). Optimal Control: Linear Quadratic Methods. Dover Publications.
- Lewis, F. L., Vrabie, D., & Syrmos, V. L. (2012). Optimal Control (3rd ed.). John Wiley & Sons.