Skip to main content

Linear Quadratic Regulator for Discrete-Time Systems

The Linear Quadratic Regulator (LQR) is one of the most important results in optimal control theory. This document presents the complete derivation and implementation of LQR for discrete-time linear systems using dynamic programming.

LQR Control System

Problem Formulation​

System Dynamics​

Consider a discrete-time linear time-varying system: xk+1=Akxk+Bkukx_{k+1} = A_k x_k + B_k u_k

Where:

  • xk∈Rnx_k \in \mathbb{R}^n: state vector at time kk
  • uk∈Rpu_k \in \mathbb{R}^p: control input at time kk
  • Ak∈Rn×nA_k \in \mathbb{R}^{n \times n}: state transition matrix
  • Bk∈Rn×pB_k \in \mathbb{R}^{n \times p}: input matrix

Quadratic Performance Function​

The objective is to minimize the quadratic cost function: J=h(xN)+∑k=0N−1g(xk,uk)J = h(x_N) + \sum_{k=0}^{N-1} g(x_k, u_k)

Where: h(xN)=12xNTSxNh(x_N) = \frac{1}{2} x_N^T S x_N g(xk,uk)=12[xkTQkxk+ukTRkuk]g(x_k, u_k) = \frac{1}{2} [x_k^T Q_k x_k + u_k^T R_k u_k]

Coefficient Convention

The factor 12\frac{1}{2} is included to simplify derivative calculations in the optimization process.

Weight Matrices​

The weight matrices must satisfy certain definiteness conditions:

Terminal weight matrix: S=[s1⋯0⋮⋱⋮0⋯sn],s1,s2,…,sn≥0S = \begin{bmatrix} s_1 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & s_n \end{bmatrix}, \quad s_1, s_2, \ldots, s_n \geq 0

State weight matrix: Qk=[q1k⋯0⋮⋱⋮0⋯qnk],q1k,q2k,…,qnk≥0Q_k = \begin{bmatrix} q_{1k} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & q_{nk} \end{bmatrix}, \quad q_{1k}, q_{2k}, \ldots, q_{nk} \geq 0

Input weight matrix: Rk=[r1k⋯0⋮⋱⋮0⋯rpk],r1k,r2k,…,rpk>0R_k = \begin{bmatrix} r_{1k} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & r_{pk} \end{bmatrix}, \quad r_{1k}, r_{2k}, \ldots, r_{pk} > 0

Matrix Requirements
  • S,QkS, Q_k: Positive semi-definite (allow zero eigenvalues)
  • RkR_k: Positive definite (all eigenvalues must be positive)

These conditions ensure the optimization problem is well-posed and has a unique solution.

Dynamic Programming Solution​

Stage N: Terminal Stage (k=Nk = N)​

At the terminal stage, the cost-to-go is: JN→N(xN)=12xNTSxNJ_{N \to N}(x_N) = \frac{1}{2} x_N^T S x_N

The optimal cost-to-go has the quadratic form: JN→N∗(xN)=12xNTP0xNJ_{N \to N}^*(x_N) = \frac{1}{2} x_N^T P_0 x_N

Where we define: P0≜SP_0 \triangleq S.

Stage N-1: One Step to Go (k=N−1→Nk = N-1 \to N)​

The cost-to-go from stage N−1N-1 to NN is:

JN−1→N(xN−1,uN−1)=12xNTSxN+12(xN−1TQN−1xN−1+uN−1TRN−1uN−1)\begin{aligned} J_{N-1 \to N}(x_{N-1}, u_{N-1}) &= \frac{1}{2} x_N^T S x_N \\ &\quad + \frac{1}{2}(x_{N-1}^T Q_{N-1} x_{N-1} + u_{N-1}^T R_{N-1} u_{N-1}) \end{aligned}

Substituting the system dynamics xN=AN−1xN−1+BN−1uN−1x_N = A_{N-1} x_{N-1} + B_{N-1} u_{N-1}:

JN−1→N(xN−1,uN−1)=12[AN−1xN−1+BN−1uN−1]TP0[AN−1xN−1+BN−1uN−1]+12(xN−1TQN−1xN−1+uN−1TRN−1uN−1)\begin{aligned} J_{N-1 \to N}(x_{N-1}, u_{N-1}) &= \frac{1}{2}[A_{N-1} x_{N-1} + B_{N-1} u_{N-1}]^T P_0 [A_{N-1} x_{N-1} + B_{N-1} u_{N-1}] \\ &\quad + \frac{1}{2}(x_{N-1}^T Q_{N-1} x_{N-1} + u_{N-1}^T R_{N-1} u_{N-1}) \end{aligned}

Optimization: Finding the Optimal Control​

To find the optimal control, we take the derivative with respect to uN−1u_{N-1} and set it to zero: ∂JN−1→N(xN−1,uN−1)∂uN−1=0\frac{\partial J_{N-1 \to N}(x_{N-1}, u_{N-1})}{\partial u_{N-1}} = 0

Derivative calculation:

For the first term, let y(uN−1)=AN−1xN−1+BN−1uN−1y(u_{N-1}) = A_{N-1} x_{N-1} + B_{N-1} u_{N-1}: ∂∂uN−1[12yTP0y]=∂y∂uN−1∂∂y[12yTP0y]=BN−1TP0y\frac{\partial}{\partial u_{N-1}} \left[\frac{1}{2} y^T P_0 y\right] = \frac{\partial y}{\partial u_{N-1}} \frac{\partial}{\partial y}\left[\frac{1}{2} y^T P_0 y\right] = B_{N-1}^T P_0 y

For the second term: ∂∂uN−1[12uN−1TRN−1uN−1]=RN−1uN−1\frac{\partial}{\partial u_{N-1}} \left[\frac{1}{2} u_{N-1}^T R_{N-1} u_{N-1}\right] = R_{N-1} u_{N-1}

Setting the derivative to zero: BN−1TP0[AN−1xN−1+BN−1uN−1]+RN−1uN−1=0B_{N-1}^T P_0 [A_{N-1} x_{N-1} + B_{N-1} u_{N-1}] + R_{N-1} u_{N-1} = 0

Solving for the optimal control: uN−1∗=−(BN−1TP0BN−1+RN−1)−1BN−1TP0AN−1xN−1u_{N-1}^* = -(B_{N-1}^T P_0 B_{N-1} + R_{N-1})^{-1} B_{N-1}^T P_0 A_{N-1} x_{N-1}

This gives us the feedback control law: uN−1∗=−FN−1xN−1u_{N-1}^* = -F_{N-1} x_{N-1}

Where the feedback gain is: FN−1=(BN−1TP0BN−1+RN−1)−1BN−1TP0AN−1F_{N-1} = (B_{N-1}^T P_0 B_{N-1} + R_{N-1})^{-1} B_{N-1}^T P_0 A_{N-1}

Verification of Minimum​

The second derivative confirms this is a minimum: ∂2JN−1→N∂uN−12=BN−1TP0BN−1+RN−1>0\frac{\partial^2 J_{N-1 \to N}}{\partial u_{N-1}^2} = B_{N-1}^T P_0 B_{N-1} + R_{N-1} > 0

Since P0=S≥0P_0 = S \geq 0 and RN−1>0R_{N-1} > 0, the Hessian is positive definite.

Cost-to-Go Matrix Update​

Substituting the optimal control back into the cost function: JN−1→N∗(xN−1)=12xN−1TP1xN−1J_{N-1 \to N}^*(x_{N-1}) = \frac{1}{2} x_{N-1}^T P_1 x_{N-1}

Where: P1=(AN−1−BN−1FN−1)TP0(AN−1−BN−1FN−1)+FN−1TRN−1FN−1+QN−1P_1 = (A_{N-1} - B_{N-1} F_{N-1})^T P_0 (A_{N-1} - B_{N-1} F_{N-1}) + F_{N-1}^T R_{N-1} F_{N-1} + Q_{N-1}

This is the discrete-time algebraic Riccati equation in recursive form.

General Recursive Solution​

For Stage k=N−jk = N-j to NN​

Optimal control: uN−j∗=−FN−jxN−ju_{N-j}^* = -F_{N-j} x_{N-j}

Feedback gain: FN−j=(BN−jTPj−1BN−j+RN−j)−1BN−jTPj−1AN−jF_{N-j} = (B_{N-j}^T P_{j-1} B_{N-j} + R_{N-j})^{-1} B_{N-j}^T P_{j-1} A_{N-j}

Cost-to-go: JN−j→N∗(xN−j)=12xN−jTPjxN−jJ_{N-j \to N}^*(x_{N-j}) = \frac{1}{2} x_{N-j}^T P_j x_{N-j}

Riccati recursion: Pj=(AN−j−BN−jFN−j)TPj−1(AN−j−BN−jFN−j)+FN−jTRN−jFN−j+QN−jP_j = (A_{N-j} - B_{N-j} F_{N-j})^T P_{j-1} (A_{N-j} - B_{N-j} F_{N-j}) + F_{N-j}^T R_{N-j} F_{N-j} + Q_{N-j}

Alternative Riccati Form​

The Riccati equation can also be written as: Pj=AN−jTPj−1AN−j+QN−j−AN−jTPj−1BN−j(BN−jTPj−1BN−j+RN−j)−1BN−jTPj−1AN−jP_j = A_{N-j}^T P_{j-1} A_{N-j} + Q_{N-j} - A_{N-j}^T P_{j-1} B_{N-j} (B_{N-j}^T P_{j-1} B_{N-j} + R_{N-j})^{-1} B_{N-j}^T P_{j-1} A_{N-j}

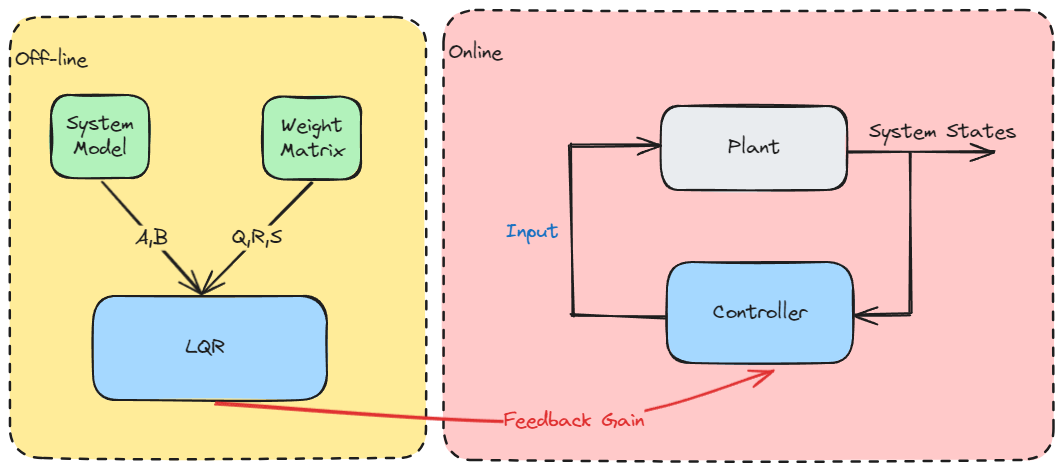
Algorithm Summary​

Backward Pass (Offline Computation)​

Initialize: P0=SP_0 = S

For j=1,2,…,Nj = 1, 2, \ldots, N:

  1. Compute feedback gain: FN−j=(BN−jTPj−1BN−j+RN−j)−1BN−jTPj−1AN−jF_{N-j} = (B_{N-j}^T P_{j-1} B_{N-j} + R_{N-j})^{-1} B_{N-j}^T P_{j-1} A_{N-j}
  2. Update Riccati matrix: Pj=(AN−j−BN−jFN−j)TPj−1(AN−j−BN−jFN−j)+FN−jTRN−jFN−j+QN−jP_j = (A_{N-j} - B_{N-j} F_{N-j})^T P_{j-1} (A_{N-j} - B_{N-j} F_{N-j}) + F_{N-j}^T R_{N-j} F_{N-j} + Q_{N-j}

Forward Pass (Online Implementation)​

Given: Initial state x0x_0

For k=0,1,…,N−1k = 0, 1, \ldots, N-1:

  1. Apply control: uk=−Fkxku_k = -F_k x_k
  2. Update state: xk+1=Akxk+Bkukx_{k+1} = A_k x_k + B_k u_k

Time-Invariant Case​

For Linear Time-Invariant (LTI) systems where Ak=AA_k = A and Bk=BB_k = B are constant:

Steady-State Solution​

As N→∞N \to \infty, the feedback gain converges to a constant: lim⁡N→∞FN−k=F∞\lim_{N \to \infty} F_{N-k} = F_{\infty}

The steady-state gain satisfies: F∞=(BTP∞B+R)−1BTP∞AF_{\infty} = (B^T P_{\infty} B + R)^{-1} B^T P_{\infty} A

Where P∞P_{\infty} is the solution to the discrete-time algebraic Riccati equation (DARE): P∞=ATP∞A+Q−ATP∞B(BTP∞B+R)−1BTP∞AP_{\infty} = A^T P_{\infty} A + Q - A^T P_{\infty} B (B^T P_{\infty} B + R)^{-1} B^T P_{\infty} A

Advantages of Steady-State Solution​

  1. Computational efficiency: No need to solve Riccati recursion online
  2. Memory savings: Store only one gain matrix instead of sequence
  3. Stability guarantees: If (A,B)(A,B) is controllable and (A,Q1/2)(A,Q^{1/2}) is observable

Implementation​

MATLAB Implementation​

function [F] = lqr_dp(A, B, Q, R, S)
% LQR solution using dynamic programming
% Inputs: A, B (system matrices), Q, R, S (weight matrices)
% Output: F (feedback gain)

    P0 = S;                    % Initialize P_[0]
    max_iter = 200;            % Maximum iterations
    tolerance = 1e-3;          % Convergence tolerance
    
    P_k_minus_1 = P0;
    F_prev = Inf;
    
    for k = 1:max_iter
        % Compute feedback gain
        F_current = (R + B' * P_k_minus_1 * B) \ (B' * P_k_minus_1 * A);
        
        % Update Riccati matrix
        P_k = (A - B * F_current)' * P_k_minus_1 * (A - B * F_current) + ...
              F_current' * R * F_current + Q;
        
        % Check convergence
        if max(abs(F_current - F_prev), [], 'all') < tolerance
            fprintf('Converged in %d iterations\n', k);
            F = F_current;
            return;
        end
        
        P_k_minus_1 = P_k;
        F_prev = F_current;
    end
    
    error('Maximum iterations exceeded');
end

Python Implementation​

import numpy as np

def lqr_dp(A, B, Q, R, S):
    """
    LQR solution using dynamic programming
    """
    P0 = S                     # Initialize P_[0]
    max_iter = 200             # Maximum iterations
    tolerance = 1e-3           # Convergence tolerance
    
    P_k_minus_1 = P0
    F_prev = np.inf
    
    for k in range(max_iter):
        # Compute feedback gain
        F_current = np.linalg.solve(
            R + B.T @ P_k_minus_1 @ B, 
            B.T @ P_k_minus_1 @ A
        )
        
        # Update Riccati matrix
        A_cl = A - B @ F_current
        P_k = A_cl.T @ P_k_minus_1 @ A_cl + F_current.T @ R @ F_current + Q
        
        # Check convergence
        if np.max(np.abs(F_current - F_prev)) < tolerance:
            print(f'Converged in {k+1} iterations')
            return F_current
            
        P_k_minus_1 = P_k
        F_prev = F_current
    
    raise ValueError('Maximum iterations exceeded')

Properties and Characteristics​

1. Optimality​

The LQR controller minimizes the quadratic cost function subject to the linear system dynamics.

2. Stability​

For the infinite-horizon case, if (A,B)(A,B) is controllable, the closed-loop system xk+1=(A−BF∞)xkx_{k+1} = (A - BF_{\infty})x_k is asymptotically stable.

3. Robustness​

LQR controllers have excellent robustness properties:

  • Gain margin: ≥6\geq 6 dB
  • Phase margin: ≥60°\geq 60°

4. Linear State Feedback​

The optimal control law is a linear function of the current state, making it easy to implement.

Design Guidelines​

Weight Matrix Selection​

State weights (QQ):

  • Larger values → tighter regulation of corresponding states
  • Zero diagonal elements → no penalty for deviations in those states

Input weights (RR):

  • Larger values → more conservative control (smaller inputs)
  • Smaller values → more aggressive control (larger inputs)

Terminal weights (SS):

  • Often chosen as solution to infinite-horizon DARE
  • Can be zero for finite-horizon problems

Tuning Process​

  1. Start with identity matrices: Q=IQ = I, R=IR = I
  2. Adjust relative weights based on performance requirements
  3. Use iterative design and simulation verification
  4. Consider physical constraints and actuator limitations

Extensions and Variations​

1. LQR with Integral Action​

Add integral states to eliminate steady-state error for step references.

2. LQG (Linear Quadratic Gaussian)​

Combine LQR with Kalman filter for systems with noise and partial state measurements.

3. Robust LQR​

Design controllers that maintain performance under model uncertainties.

4. Constrained LQR​

Handle input and state constraints using model predictive control (MPC).

References​

  1. Optimal Control by DR_CAN
  2. Wang, T. (2023). 控制之美 (卷2). Tsinghua University Press.
  3. Anderson, B. D. O., & Moore, J. B. (2007). Optimal Control: Linear Quadratic Methods. Dover Publications.
  4. Lewis, F. L., Vrabie, D., & Syrmos, V. L. (2012). Optimal Control (3rd ed.). John Wiley & Sons.
  5. Åström, K. J., & Murray, R. M. (2021). Feedback Systems: An Introduction for Scientists and Engineers (2nd ed.). Princeton University Press.