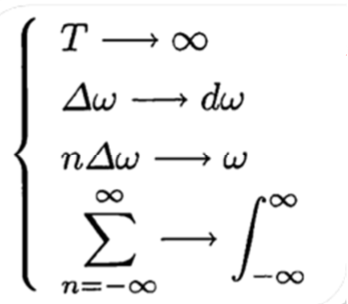Skip to main content

フーリエ変換

フーリエ変換は、フーリエ級数を非周期信号に拡張した数学的手法です。任意の信号を周波数成分に分解し、時間領域と周波数領域を結ぶ重要な橋渡しの役割を果たします。

フーリエ級数からフーリエ変換への導出​

複素フーリエ級数の拡張​

複素フーリエ級数の cnc_n を f(t)f(t) に代入すると：

f(t)=∑n=−∞∞[1T∫−T2T2f(t)e−j2πnTtdt]ej2πnTtf(t) = \sum_{n=-\infty}^{\infty} \left[\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}} f(t)e^{-j2\pi \frac{n}{T} t}dt\right]e^{j2\pi \frac{n}{T}t}

基本周波数を ω0\omega_0 とすると：

1T=ω02π\frac{1}{T} = \frac{\omega_0}{2\pi}

これを代入すると：

f(t)=12π∑n=−∞∞[ω0∫−T2T2f(t)e−jnω0tdt]ejnω0tf(t) = \frac{1}{2\pi}\sum_{n=-\infty}^{\infty} \left[\omega_0\int_{-\frac{T}{2}}^{\frac{T}{2}} f(t)e^{-jn\omega_0 t}dt\right]e^{jn\omega_0 t}

非周期信号への拡張​

周期 TT が非常に大きくなると、基本角周波数は非常に小さくなり、ω0=Δω\omega_0 = \Delta\omega と表現できます。

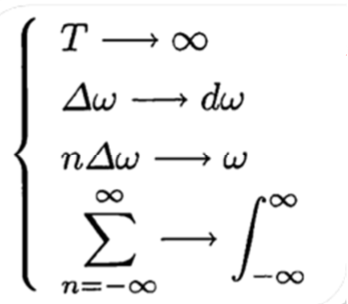
フーリエ変換の概念

T→∞T \to \infty の極限を取ると、離散的な周波数成分が連続的になり：

f(t)=12π∫−∞∞[∫−∞∞f(t)e−jωtdt]ejωtdωf(t) = \frac{1}{2\pi}\int_{-\infty}^{\infty} \left[\int_{-\infty}^{\infty} f(t)e^{-j\omega t}dt \right]e^{j\omega t}d\omega

フーリエ変換​

定義​

フーリエ変換：

F(ω)=∫−∞∞f(t)e−jωtdtF(\omega) = \int_{-\infty}^{\infty} f(t)e^{-j\omega t}dt

この変換により、時間関数 f(t)f(t) を周波数関数 F(ω)F(\omega) に変換します。

フーリエ変換の意味
  • 時間領域の信号を周波数領域で表現
  • 各周波数成分の振幅と位相情報を含む
  • 非周期信号（単発波）を扱える

逆フーリエ変換​

逆フーリエ変換：

f(t)=12π∫−∞∞F(ω)ejωtdωf(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} F(\omega)e^{j\omega t}d\omega

この変換により、周波数関数 F(ω)F(\omega) から元の時間関数 f(t)f(t) を復元します。

フーリエ変換対

フーリエ変換と逆フーリエ変換は対になっており、以下の記号で表されます： f(t)↔FF(ω)f(t) \overset{\mathcal{F}}{\leftrightarrow} F(\omega)

フーリエ変換の性質​

フーリエ変換は多くの重要な性質を持ちます：

線形性（Linearity）​

F[af(t)+bg(t)]=aF(ω)+bG(ω)\mathcal{F}[af(t) + bg(t)] = aF(\omega) + bG(\omega)

ここで a,ba, b は定数です。

時間軸の移動（時間シフト）​

F[f(t−τ)]=e−jωτF(ω)\mathcal{F}[f(t-\tau)] = e^{-j\omega\tau}F(\omega)

時間軸での移動は、周波数領域では位相の変化として現れます。

周波数軸の移動（周波数シフト）​

F[f(t)ejω0t]=F(ω−ω0)\mathcal{F}[f(t)e^{j\omega_0t}] = F(\omega - \omega_0)

時間領域での複素指数関数の乗算は、周波数領域での周波数シフトに対応します。

相対性（Duality）​

逆フーリエ変換において、両辺に 2π2\pi をかけ、ω→t\omega \to t、t→−ωt \to -\omega の置き換えを行うと：

f(t)=12π∫−∞∞F(ω)ejωtdω→2πf(−ω)=∫−∞∞F(t)ejt(−ω)dtf(t) = \frac{1}{2\pi}\int_{-\infty}^{\infty}F(\omega)e^{j\omega t}d\omega \to 2\pi f(-\omega) = \int_{-\infty}^{\infty}F(t)e^{jt(-\omega)}dt

したがって： 2πf(−ω)↔F(t)2\pi f(-\omega) \leftrightarrow F(t)

相対性の意味

時間と周波数の役割を入れ替えても、変換の形式が保たれることを示しています。これはフーリエ変換の美しい対称性の一つです。

その他の重要な性質​

微分の性質​

F[df(t)dt]=jωF(ω)\mathcal{F}\left[\frac{df(t)}{dt}\right] = j\omega F(\omega)

時間微分は周波数領域では jωj\omega の乗算に対応します。

積分の性質​

F[∫−∞tf(τ)dτ]=F(ω)jω+πF(0)δ(ω)\mathcal{F}\left[\int_{-\infty}^{t} f(\tau)d\tau\right] = \frac{F(\omega)}{j\omega} + \pi F(0)\delta(\omega)

畳み込み定理​

F[f(t)∗g(t)]=F(ω)G(ω)\mathcal{F}[f(t) * g(t)] = F(\omega)G(\omega)

時間領域での畳み込みは、周波数領域では単純な乗算になります。

パーセバルの定理​

∫−∞∞∣f(t)∣2dt=12π∫−∞∞∣F(ω)∣2dω\int_{-\infty}^{\infty} |f(t)|^2 dt = \frac{1}{2\pi}\int_{-\infty}^{\infty} |F(\omega)|^2 d\omega

時間領域と周波数領域でエネルギーが保存されることを示します。

応用例​

インパルス関数​

ディラックのデルタ関数： δ(t)↔1\delta(t) \leftrightarrow 1

デルタ関数のフーリエ変換は定数1になります。

矩形関数​

矩形関数： rect(t)↔sinc(ω)\text{rect}(t) \leftrightarrow \text{sinc}(\omega)

矩形関数のフーリエ変換はsinc関数になります。

指数関数​

減衰指数関数： e−atu(t)↔1a+jω(a>0)e^{-at}u(t) \leftrightarrow \frac{1}{a + j\omega} \quad (a > 0)

ここで u(t)u(t) は単位ステップ関数です。

工学的意義​

信号処理への応用​

  1. スペクトラム解析：信号の周波数成分を分析
  2. フィルタ設計：周波数特性の設計と解析
  3. システム解析：線形システムの周波数応答
  4. 画像処理：2次元フーリエ変換による画像解析

制御工学への応用​

  1. 周波数応答：システムの周波数特性の解析
  2. 安定性解析：ナイキスト線図との関連
  3. フィルタ設計：ノイズ除去や信号整形

まとめ​

フーリエ変換は信号処理と制御工学の基礎となる重要な数学的ツールです：

  1. 拡張性：フーリエ級数を非周期信号に拡張
  2. 双方向性：時間領域と周波数領域の相互変換
  3. 豊富な性質：線形性、時間シフト、周波数シフトなど
  4. 広範な応用：信号処理、システム解析、フィルタ設計

次章では、ディジタル信号処理で使用される離散フーリエ変換について学習します。

次のステップ
  • 離散フーリエ変換（DFT）：ディジタル信号への適用
  • 高速フーリエ変換（FFT）：効率的な計算手法
  • Z変換：離散時間システムの解析
  • ラプラス変換：微分方程式の解法と制御理論