離散時間システム

離散時間システムは、ディジタル信号処理の基盤となる概念です。アナログ信号をディジタル化して処理するための理論的基礎から、実際のシステム設計まで幅広くカバーします。

サンプリング定理（標本化定理）

ナイキスト・シャノンのサンプリング定理

サンプリング定理または標本化定理とも呼ばれ、シャノンによって確立されました。

サンプリング定理の要求

信号成分の最大周波数の2倍より高いサンプリング周波数を取るべきです。

信号 $x(t)$ の成分の最大角周波数 $\omega_M$ が以下の条件を満たすとき、サンプリング定理を満たします：

$\omega_M < \frac{\omega_s}{2} = \frac{\pi}{T}$

すなわち： $\omega_s > 2\omega_M$

ここで：

• $\omega_s$：サンプリング角周波数
• $T$：サンプリング周期
• $\omega_M$：信号の最大角周波数

ナイキスト周波数

$\omega_s/2$ をナイキスト周波数と呼びます。これを超える周波数成分はエイリアシング（折り返し雑音）を引き起こします。

伝達関数

線形差分方程式

線形な離散時間システムの出力は、これまでの出力と入力を用いて、一般的に以下のような線形差分方程式で表すことができます：

$y(n) + a_1y(n-1) + a_2y(n-2) + \cdots + a_Iy(n-I)$ $= b_0x(n) + b_1x(n-1) + b_2x(n-2) + \cdots + b_Jx(n-J)$

Z変換による伝達関数

初期値を0として、Z変換を適用すると：

$Y(z) + a_1Y(z)z^{-1} + a_2Y(z)z^{-2} + \cdots + a_IY(z)z^{-I}$ $= b_0X(z) + b_1X(z)z^{-1} + b_2X(z)z^{-2} + \cdots + b_JX(z)z^{-J}$

したがって、離散時間システムの伝達関数は：

$H(z) = \frac{Y(z)}{X(z)} = \frac{b_0 + b_1z^{-1} + b_2z^{-2} + \cdots + b_Jz^{-J}}{1 + a_1z^{-1} + a_2z^{-2} + \cdots + a_Iz^{-I}}$

極と零点

• 零点：分子多項式 = 0 を満たす $z$
• 極：分母多項式 = 0 を満たす $z$

インパルス応答

連続時間システムとの類推

連続時間システムでは：

• 入力 $u(t) = \delta(t)$ をラプラス変換による微分方程式に代入
• 出力 $Y(s) = H(s)$（伝達関数）
• インパルス応答 $h(t)$ は伝達関数の逆ラプラス変換

離散時間システムのインパルス応答

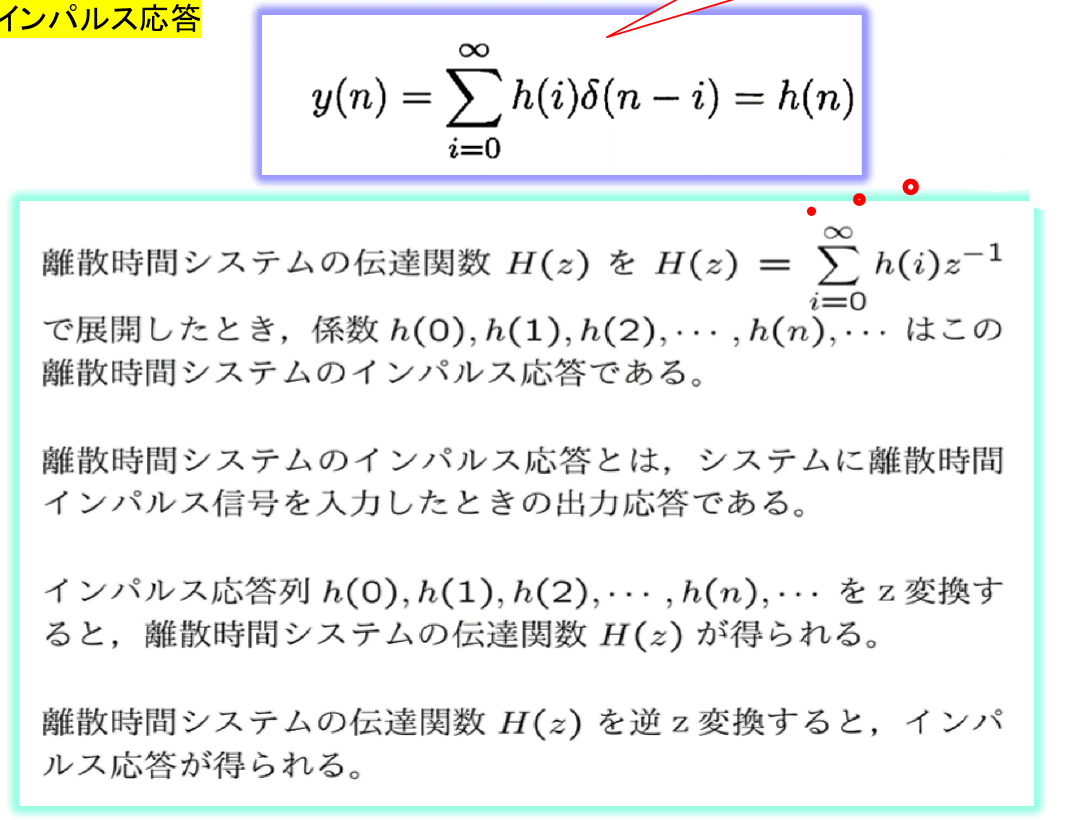
離散時間システムでは：

• 入力 $x(n) = \delta(n)$（離散デルタ関数）
• 出力 $Y(z) = H(z)$
• インパルス応答 $h(n)$ は伝達関数の逆Z変換

$h(n) = \mathcal{Z}^{-1}[H(z)]$

システムの分類：IIRとFIR

IIR（Infinite Impulse Response）システム

• 無限インパルス応答
• 伝達関数 $H(z)$ に分母がある
• 巡回型システム
• フィードバックを持つ

特徴：

• 少ない係数で急峻な特性を実現
• 位相特性が非線形
• 安定性の考慮が必要

FIR（Finite Impulse Response）システム

• 有限インパルス応答
• 伝達関数 $H(z)$ に分母がない
• 非巡回型システム
• フィードフォワードのみ

特徴：

• 常に安定
• 線形位相特性を実現可能
• 設計が比較的容易

システム選択の指針

• 急峻な特性が必要：IIRシステム
• 線形位相が重要：FIRシステム
• 安定性が最優先：FIRシステム

ディジタル信号処理の基本要素

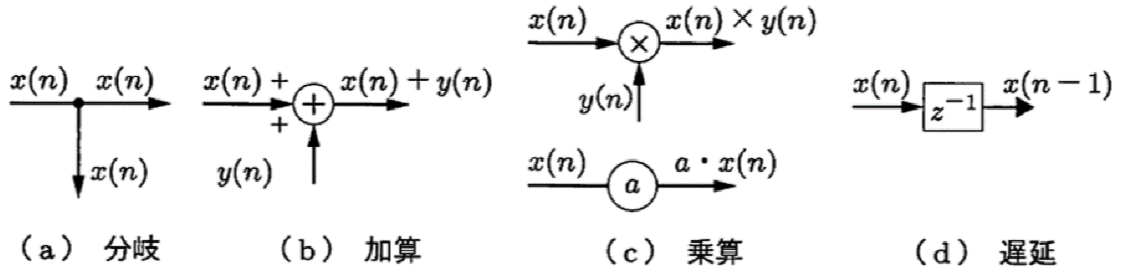
ディジタル信号処理システムの基本要素：

1. 加算器：信号の加算
2. 乗算器：定数との乗算
3. 遅延素子：$z^{-1}$（1サンプル遅延）

離散時間畳み込み（時間域）

一般的な畳み込み

$y(n) = \sum_{k=-\infty}^{\infty} x(k)h(n-k)$

因果律を考慮した畳み込み

実際のシステムでは因果律を考慮する必要があります：

入力信号のみが因果律を満たす場合： $y(n) = \sum_{k=0}^{\infty} x(k)h(n-k)$

システムのみが因果律を満たす場合： $y(n) = \sum_{k=-\infty}^{n} x(k)h(n-k)$

入力信号とシステムの両方が因果律を満たす場合： $y(n) = \sum_{k=0}^{n} x(k)h(n-k)$

畳み込みの対称性

$y(n) = \sum_{k=0}^{n} x(k)h(n-k) = \sum_{k=0}^{n} x(n-k)h(k)$

畳み込みの物理的意味

畳み込みは、システムの記憶効果を表現します。現在の出力は、過去のすべての入力とシステムの応答の重み付き和として計算されます。

周波数応答

周波数応答の定義

伝達関数 $H(z)$ に $z = e^{j\omega T}$ を代入：

$H(e^{j\omega T}) = |H(e^{j\omega T})| e^{j\theta(\omega)}$

振幅特性

$|H(e^{j\omega T})| = \sqrt{[\text{Re}\{H(e^{j\omega T})\}]^2 + [\text{Im}\{H(e^{j\omega T})\}]^2}$

位相特性

$\theta(\omega) = \arg(H(e^{j\omega T})) = \tan^{-1}\left[\frac{\text{Im}\{H(e^{j\omega T})\}}{\text{Re}\{H(e^{j\omega T})\}}\right]$

群遅延

$\tau(\omega) = -\frac{\partial\theta(\omega)}{\partial\omega}$

群遅延は、信号の各周波数成分がシステムを通過する際の遅延時間を表します。

群遅延の重要性

通信システムや音響システムでは、群遅延の平坦性が信号の歪みを防ぐために重要です。

離散時間システムの安定性

連続時間との対応

連続時間システム： $G(s) \rightarrow G(j\omega), \quad s = j\omega$

離散時間システム： $H(z) \rightarrow H(e^{j\omega T}), \quad z = e^{j\omega T}$

写像関係

$z = e^{sT} = e^{j\omega T}$

$s = \sigma + j\omega$ において、$\sigma = 0$ のとき $|e^{j\omega T}| = 1$

s平面の虚数軸は、z平面の単位円に写像される

安定性判別

離散時間システムの安定性は極の位置で決まります：

• 安定：すべての極の絶対値が1より小さい（$|z_i| < 1$）
• 安定限界：極の絶対値が1に等しい（$|z_i| = 1$）
• 不安定：極の絶対値が1より大きい（$|z_i| > 1$）

安定性の直感的理解

• 単位円内：時間とともに減衰（安定）
• 単位円上：振動が持続（安定限界）
• 単位円外：時間とともに発散（不安定）

まとめ

離散時間システムは、ディジタル信号処理の基礎となる重要な概念です：

1. サンプリング定理：アナログ信号のディジタル化における基本原理
2. 伝達関数：システムの入出力関係の数学的表現
3. インパルス応答：システムの特性を表す基本的な応答
4. 安定性：実用的なシステム設計における重要な考慮事項

次章では、これらの理論を基にしたフィルタ設計について詳しく学習します。

次のステップ

• ディジタルフィルタ設計：理論の実用的応用
• FIRフィルタ設計：窓関数法と周波数サンプリング法
• IIRフィルタ設計：アナログフィルタからの変換
• 適応フィルタ：時変システムへの対応