確率分布 (Probability Distributions)
Made by Youkoutaku
確率分布は統計学と確率論の基礎概念です。この記事では、Pythonのscipyライブラリを使用して様々な確率分布を実装し、理論値と実測値を比較しながら各分布の特性を理解していきます。
ライブラリのインポート
# Library Import
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import bernoulli, binom, geom, nbinom, poisson, hypergeom, uniform, norm, expon, gamma, chi2
確率分布の種類
離散分布
bernoulli: ベルヌーイ分布binom: 2項分布geom: 幾何分布nbinom: 負の2項分布poisson: ポアソン分布hypergeom: 超幾何分布
連続分布
uniform: 一様分布norm: 正規分布gamma: ガンマ分布chi2: カイ二乗分布
主要メソッド
rvs: 確率変数の生成pmf: 確率関数(離散)pdf: 確率密度関数(連続)
1. 離散確率分布
1.1 ベルヌーイ分布
ベルヌーイ分布は、1回の試行で成功または失敗の2つの結果しかない離散確率分布です。確率パラメータ を設定し、それに従う疑似乱数列を生成します。
1.1.1
疑似乱数数列での分布関数と確率関数:
p = 0.5 # Probability
rv_bernoulli = bernoulli(p)
data_bernoulli = rv_bernoulli.rvs(size=1000) # size=1000
# Random Variable
plt.hist(data_bernoulli, alpha=0.7)
plt.title('Bernoulli Distribution')
plt.xlabel('Value')
plt.ylabel('Times')
plt.show()
# Probability mass function
x = np.linspace(0, 1, 100)
y = bernoulli.pmf(x, p)
plt.plot(x, y, 'ro', ms=8)
plt.vlines(x, 0, y, colors='r', lw=3, alpha=0.5)
plt.xlabel('Value')
plt.ylabel('p(x)')
plt.show()
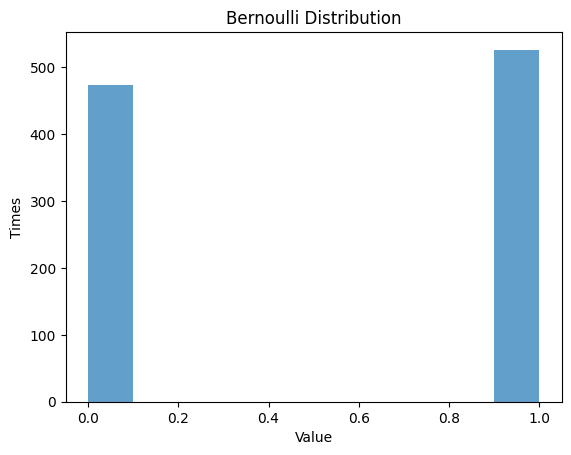
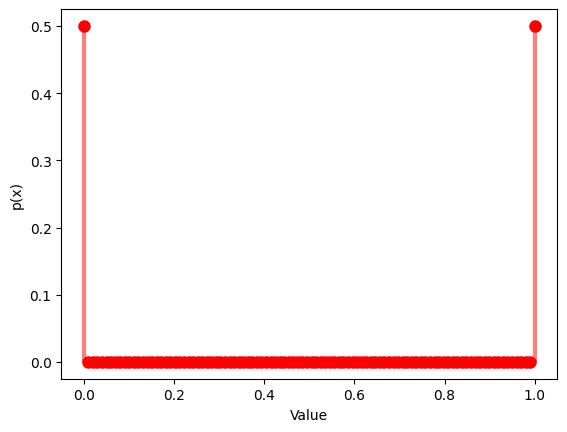
特性値:
theoretical_mean = p
theoretical_std = np.sqrt(p * (1 - p))
# Calculation of actual values
mean_bernoulli = np.mean(data_bernoulli)
std_bernoulli = np.std(data_bernoulli)
# Comparison of theoretical and measured values
print("Bernoulli Distribution:")
print("Theoretical Mean:", theoretical_mean)
print("Computed Mean:", mean_bernoulli)
print("Theoretical Standard Deviation:", theoretical_std)
print("Computed Standard Deviation:", std_bernoulli)
1.1.2
p = 0.1 # probability
rv_bernoulli = bernoulli(p)
data_bernoulli = rv_bernoulli.rvs(size=1000) # size=1000
# Random Variable
plt.hist(data_bernoulli, alpha=0.7)
plt.title('Bernoulli Distribution')
plt.xlabel('Value')
plt.ylabel('Times')
plt.grid(True)
plt.show()
# Probability mass function
x = np.linspace(0, 1, 100)
y = bernoulli.pmf(x, p)
plt.plot(x, y, 'ro', ms=8)
plt.vlines(x, 0, y, colors='r', lw=3, alpha=0.5)
plt.xlabel('Value')
plt.ylabel('p(x)')
plt.show()
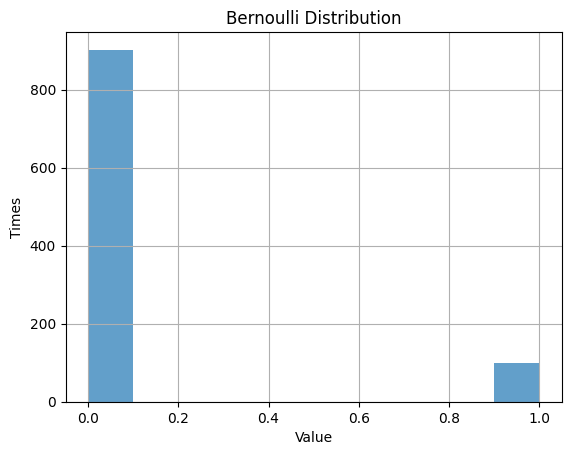
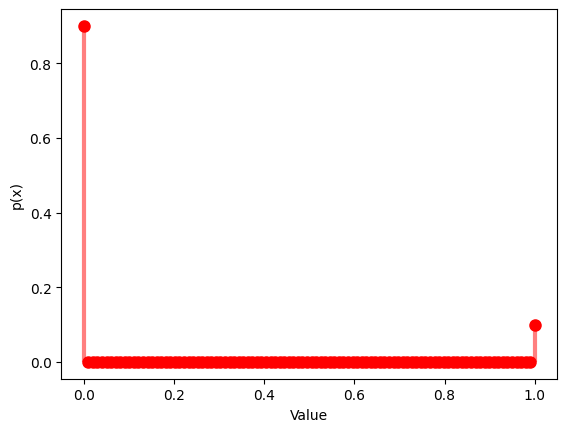
実測値の平均と標本誤差は理論値とほぼ同じであることが確認できます。
1.2 2項分布
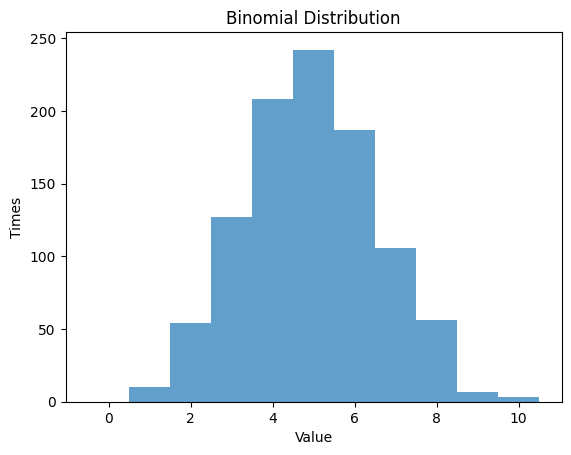
2項分布は、独立したベルヌーイ試行を複数回行った場合の成功回数の確率分布です。成功確率 と試行回数 の2つのパラメータを設定し、その分布を観察します。
1.2.1 ,
n = 10 # number of random experiments
p = 0.5 # probability
# Random Variable
rv_binom = binom(n, p)
data_binom = rv_binom.rvs(size=1000)
plt.hist(data_binom, bins=np.arange(-0.5, n+1, 1), alpha=0.7)
plt.title('Binomial Distribution')
plt.xlabel('Value')
plt.ylabel('Times')
plt.show()
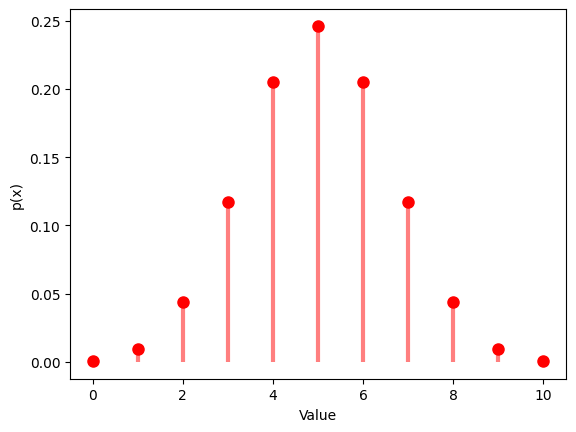
# Probability mass function
x = np.arange(0, 11)
y = binom.pmf(x, n, p)
plt.plot(x, y, 'ro', ms=8)
plt.vlines(x, 0, y, colors='r', lw=3, alpha=0.5)
plt.xlabel('Value')
plt.ylabel('p(x)')
plt.show()
1.2.2 ,
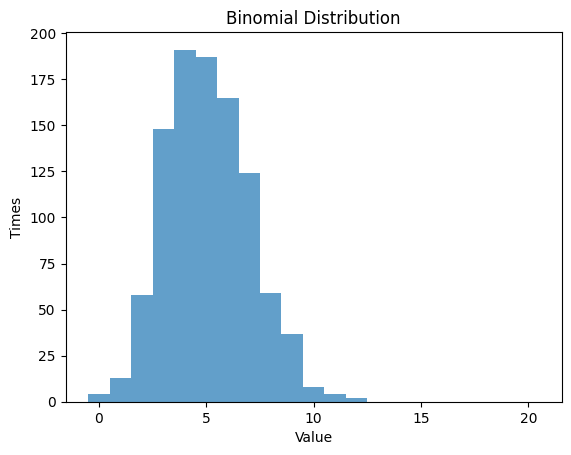
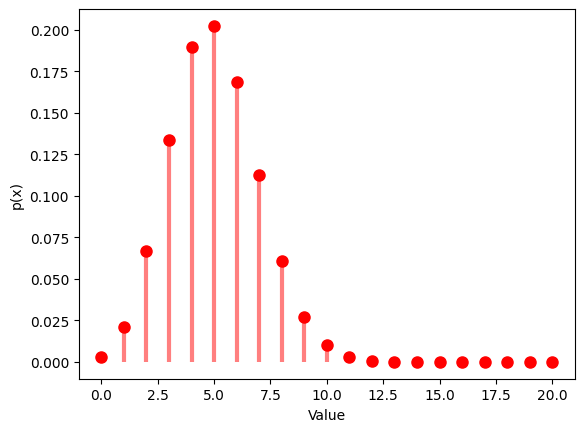
1.3 幾何分布
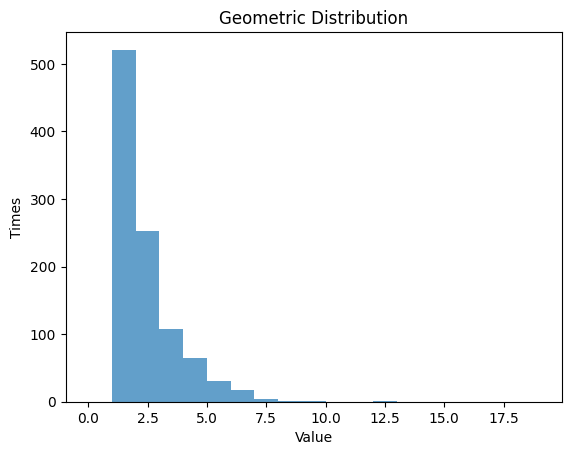
幾何分布は、最初の成功までの試行回数の確率分布です。成功確率 を設定し、その分布を観察します。
1.3.1
p = 0.5
rv_geom = geom(p)
data_geom = rv_geom.rvs(size=1000)
# Random Variable
plt.hist(data_geom, bins=np.arange(0, 20, 1), alpha=0.7)
plt.title('Geometric Distribution')
plt.xlabel('Value')
plt.ylabel('Times')
plt.show()
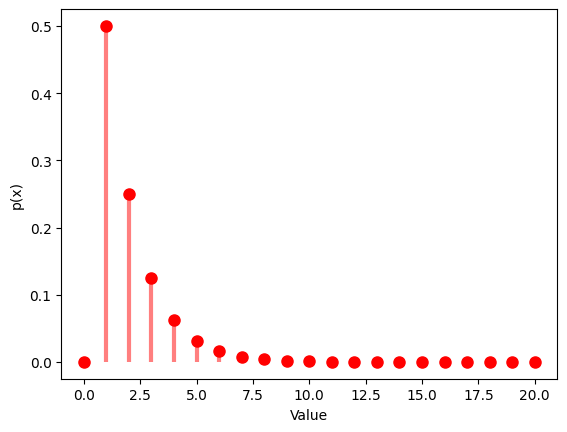
# Probability mass function
x = np.arange(0, 21)
y = geom.pmf(x, p)
plt.plot(x, y, 'ro', ms=8)
plt.vlines(x, 0, y, colors='r', lw=3, alpha=0.5)
plt.xlabel('Value')
plt.ylabel('p(x)')
plt.show()
1.3.2
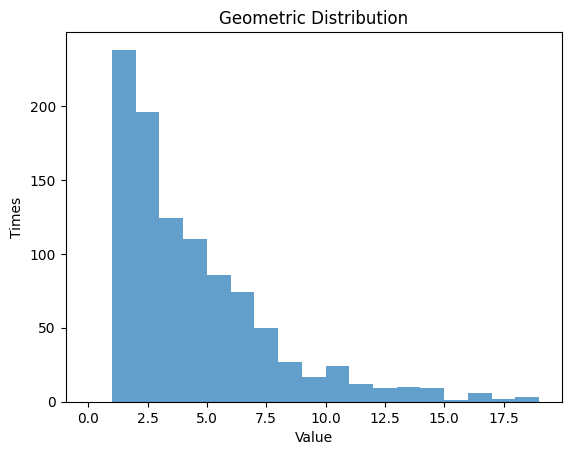
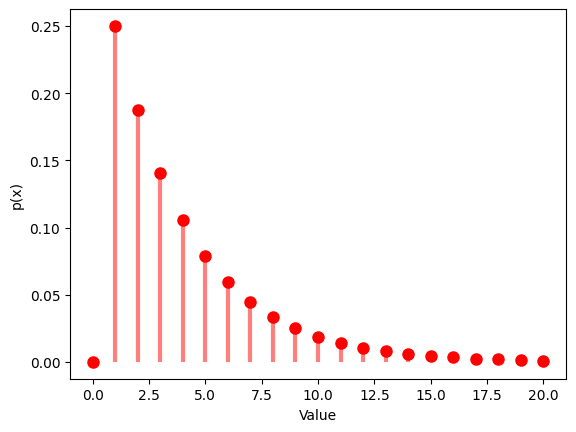
1.4 負の2項分布
負の2項分布は、成功回数が一定の値 に到達するまでのベルヌーイ試行の回数の確率分布です。成功確率 と成功回数 の2つのパラメータを設定し、その分布を観察します。
1.4.1 ,
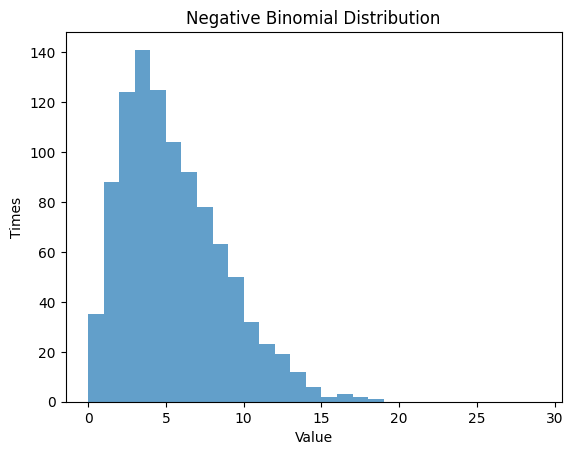
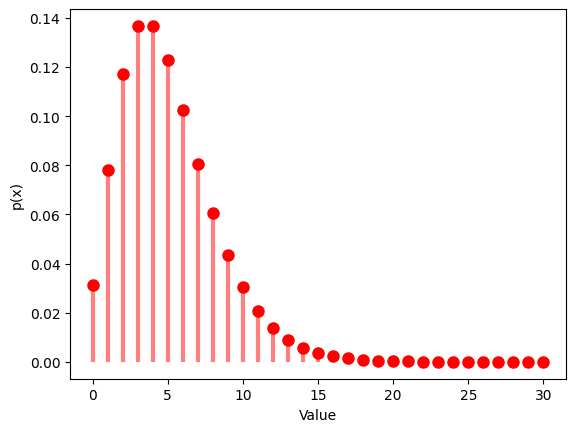
1.4.2 ,
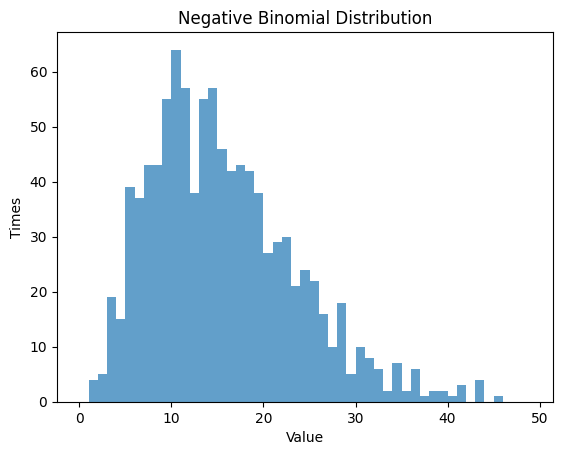
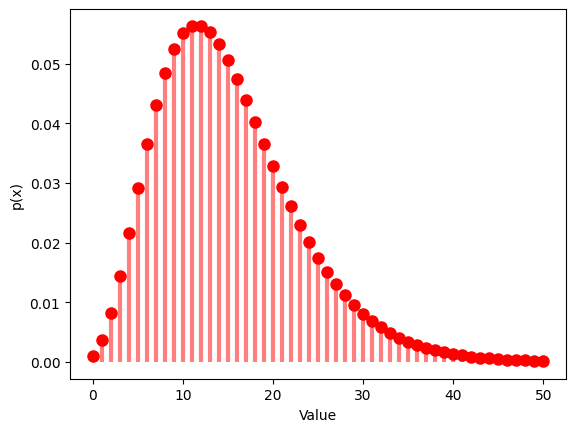
1.5 ポアソン分布
ポアソン分布は、ある一定の時間や領域内で起こる事象の発生回数の確率分布です。平均発生率 を設定し、その分布を観察します。
1.5.1
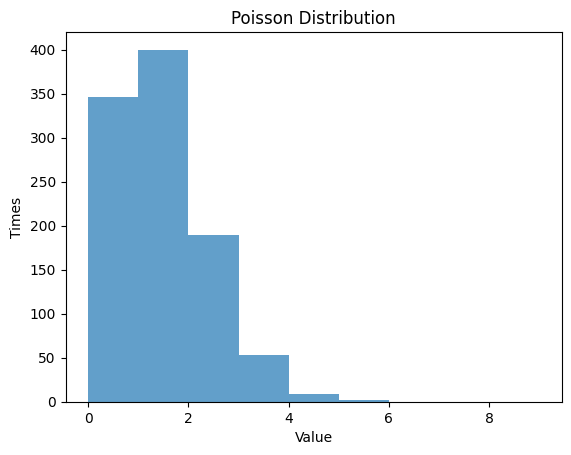
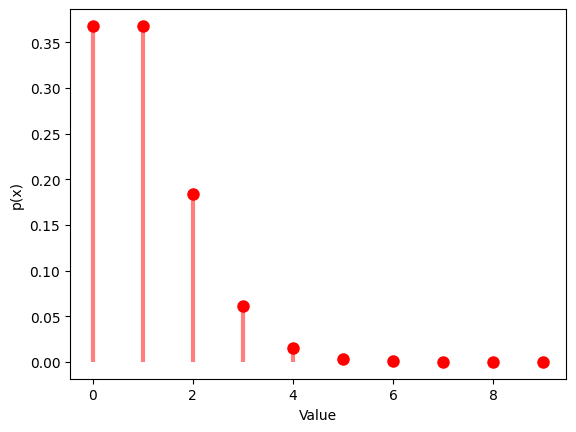
1.5.2
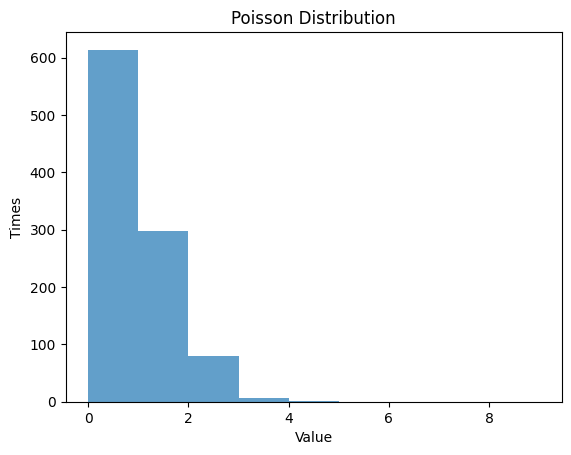
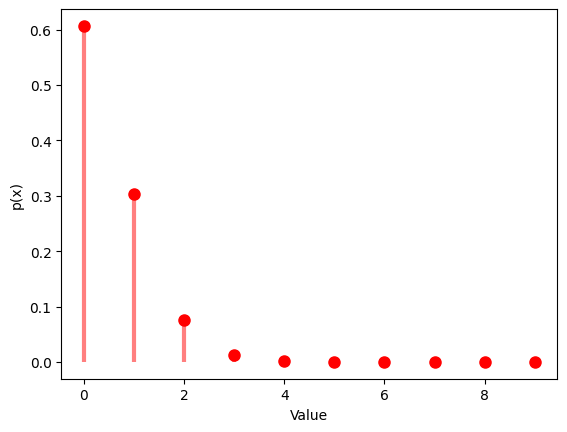
1.6 超幾何分布
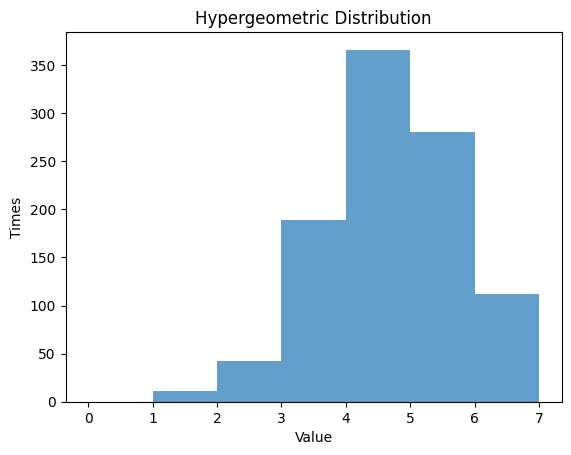
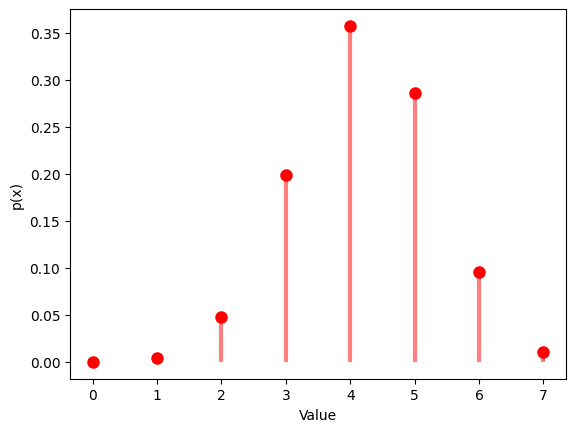
超幾何分布は、有限個の要素の中から非復元抽出した場合、成功の数が従う確率分布です。要素数 、成功の数 、抽出の数 を設定し、その分布を観察します。
1.6.1 , ,
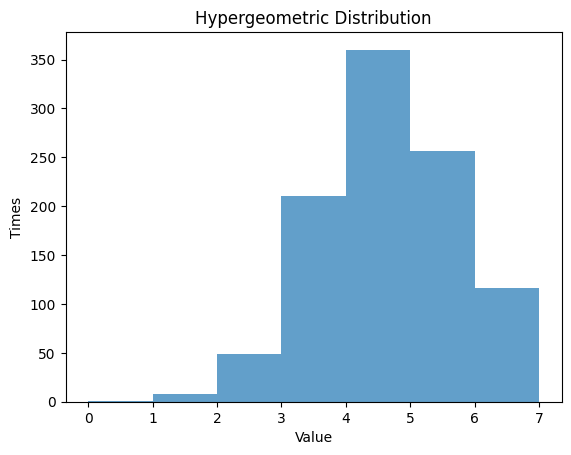
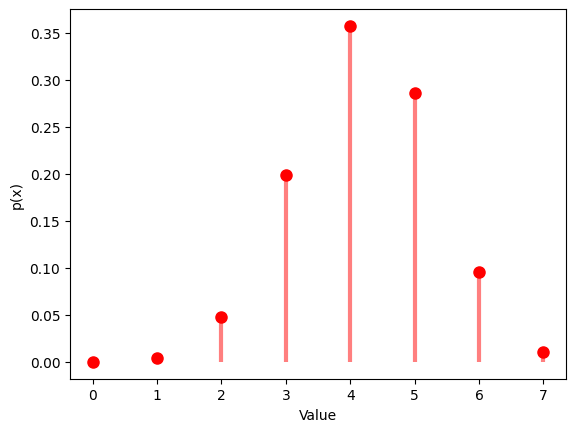
1.6.2 , ,
2. 連続確率分布
2.1 一様分布
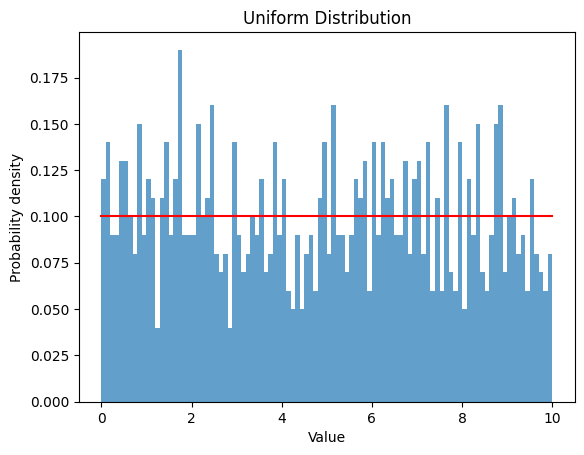
一様分布は、範囲内の値がすべて同じ確率で起こる確率分布です。下限 と上限 を設定し、その分布を観察します。
2.1.1 ,
a = 0
b = 10
rv_uniform = uniform(a, b)
data_uniform = rv_uniform.rvs(size=1000)
plt.hist(data_uniform, bins=np.arange(a, b+0.1, 0.1), density=True, alpha=0.7)
x = np.linspace(a, b, 1000)
y = uniform.pdf(x, a, b-a)
plt.plot(x, y, color='red')
plt.title('Uniform Distribution')
plt.xlabel('Value')
plt.ylabel('Probability density')
plt.show()
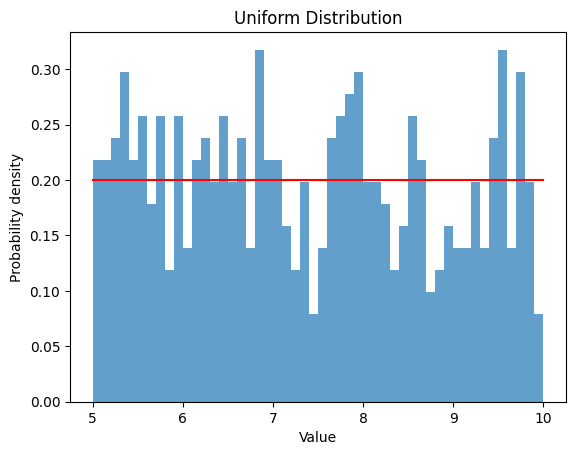
2.1.2 ,
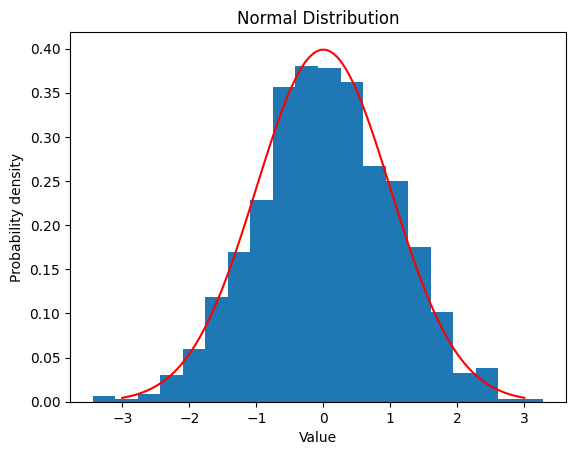
2.2 正規分布
釣り鐘型の分布です。
平均値 と標準偏差 を設定し、その分布を観察します。
2.2.1 ,
mean = 0
std = 1
data_norm = norm.rvs(loc=mean, scale=std, size=1000)
plt.hist(data_norm, bins=20, density=True)
x = np.linspace(mean - 3*std, mean + 3*std, 100)
y = norm.pdf(x, loc=mean, scale=std)
plt.plot(x, y, color='red')
plt.xlabel('Value')
plt.ylabel('Probability density')
plt.title('Normal Distribution')
plt.show()
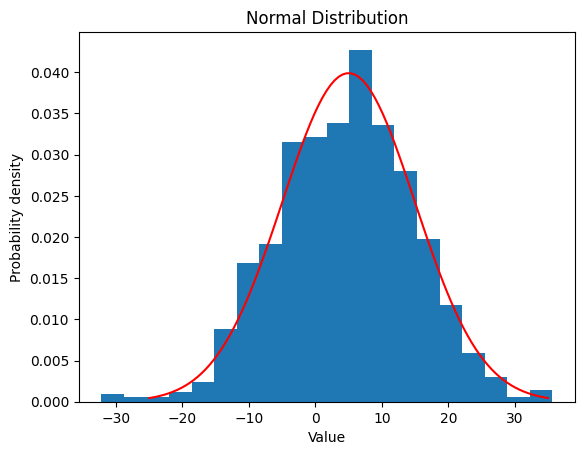
2.2.2 ,
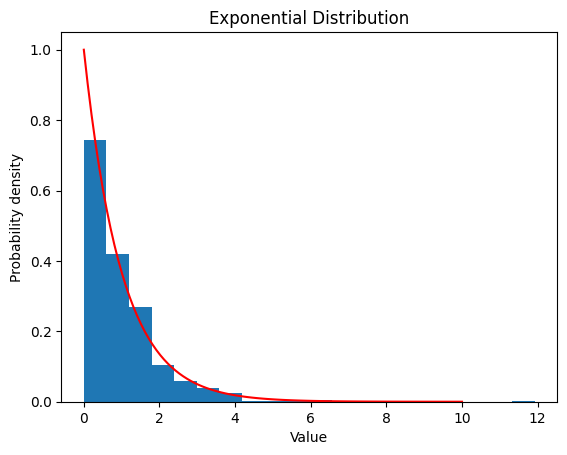
2.3 指数分布
2.3.1
lambda_ = 1
data_expon = expon.rvs(scale=1/lambda_, size=1000)
plt.hist(data_expon, bins=20, density=True)
x = np.linspace(0, 10, 100)
y = expon.pdf(x, scale=1/lambda_)
plt.plot(x, y, color='red')
plt.xlabel('Value')
plt.ylabel('Probability density')
plt.title('Exponential Distribution')
plt.show()
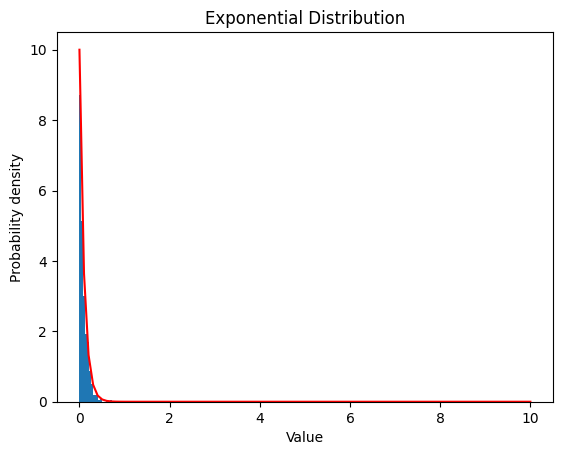
2.3.2
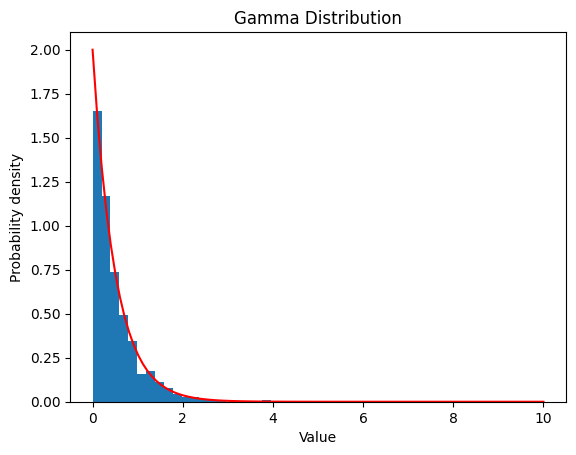
2.4 ガンマ分布
2.4.1 ,
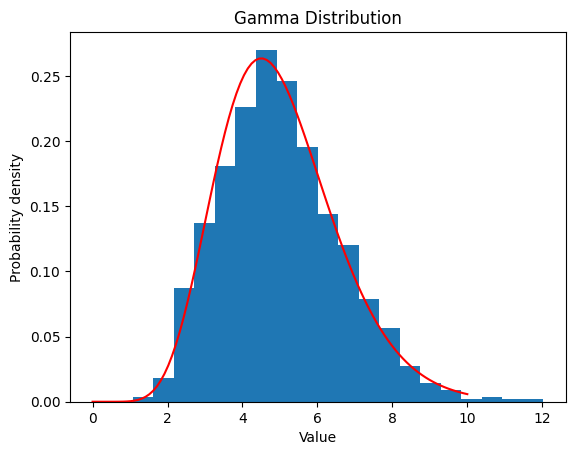
2.4.2 ,
2.5 カイ二乗分布
2.5.1
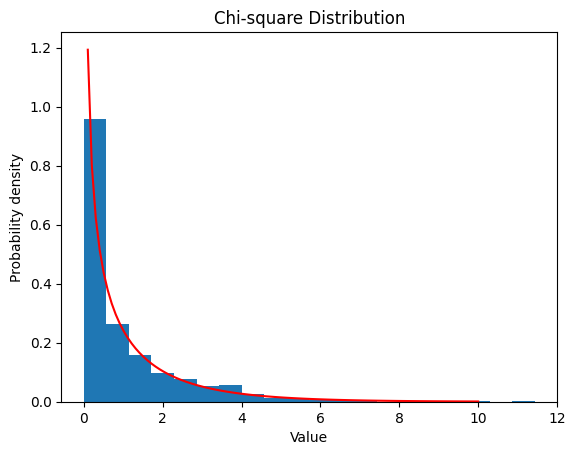
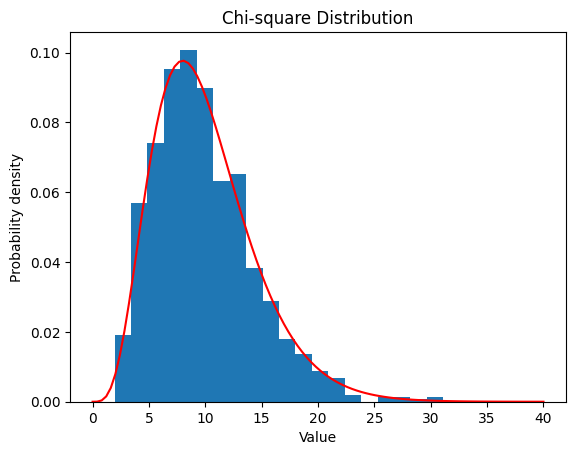
2.5.2
まとめ
この記事では、様々な確率分布について実装と可視化を行いました。各分布の特徴を理解し、理論値と実測値の比較を通じて確率分布の本質を学ぶことができました。
主要な学習ポイント
- 離散分布と連続分布の違い: 確率関数(PMF)と確率密度関数(PDF)の概念
- パラメータの影響: 各分布のパラメータが形状にどのような影響を与えるか
- 理論値と実測値の一致: 大数の法則による理論値への収束
- 実装スキル: SciPyライブラリを使った確率分布の効率的な実装
これらの確率分布は以下の分野で広く活用されています:
- 機械学習: ベイズ統計、生成モデル
- 金融工学: リスク管理、オプション価格モデル
- 品質管理: 統計的品質管理、信頼性工学
- 自然科学: 物理現象のモデリング、生物統計
確率分布の理解を深めるために、以下の学習を推奨します:
- 中心極限定理の理解と実装
- ベイズ統計の基礎
- 確率分布の組み合わせと変換
- 実データへの分布フィッティング