Skip to main content

三角形内部の点の判別

コンピュータグラフィックスや画像処理において、ある点が三角形の内部にあるかどうかを判別することは重要な処理です。この記事では、外積を使った効率的な判別方法について解説します。

三角形の線の方程式​

まず、与えられた三角形の各頂点 (x1,y1)(x_1, y_1), (x2,y2)(x_2,y_2), (x3,y3)(x_3,y_3) を通る直線の方程式を求めます。

  1. 頂点 (x1,y1)(x_1, y_1) から (x2,y2)(x_2, y_2) への直線の方程式：

    (y2−y1)(x−x1)−(x2−x1)(y−y1)=0(y_2 - y_1)(x-x_1) - (x_2 - x_1)(y-y_1)=0

  2. 頂点 (x2,y2)(x_2, y_2) から (x3,y3)(x_3, y_3) への直線の方程式：

    (y3−y2)(x−x2)−(x3−x2)(y−y2)=0(y_3 - y_2)(x-x_2) - (x_3 - x_2)(y-y_2)=0

  3. 頂点 (x3,y3)(x_3, y_3) から (x1,y1)(x_1, y_1) への直線の方程式：

    (y1−y3)(x−x3)−(x1−x3)(y−y3)=0(y_1 - y_3)(x-x_3) - (x_1 - x_3)(y-y_3) =0

これらの方程式は、ベクトルの外積の意味があります。

外積による位置判別​

ベクトル：

  • a=(x2−x1,y2−y1)a=(x_2 - x_1, y_2 - y_1)
  • b=(x3−x2,y3−y2)b=(x_3 - x_2, y_3 - y_2)
  • c=(x1−x3,y1−y3)c=(x_1 - x_3, y_1 - y_3)
  • p=(x−x1,y−y1)p=(x - x_1, y - y_1)
  • q=(x−x2,y−y2)q=(x - x_2, y - y_2)
  • h=(x−x3,y−y3)h=(x - x_3, y - y_3)

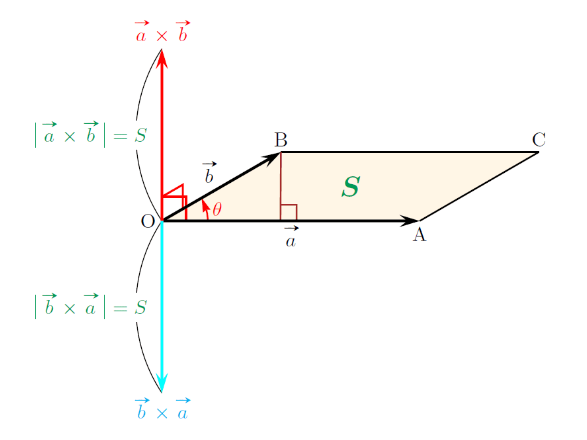
外積の式：

  1. L1=p×a=(y2−y1)(x−x1)−(x2−x1)(y−y1)L_1=p \times a =(y_2 - y_1)(x-x_1) - (x_2 - x_1)(y-y_1)

  2. L2=q×b=(y3−y2)(x−x2)−(x3−x2)(y−y2)L_2=q \times b =(y_3 - y_2)(x-x_2) - (x_3 - x_2)(y-y_2)

  3. L3=h×c=(y1−y3)(x−x3)−(x1−x3)(y−y3)L_3=h \times c=(y_1 - y_3)(x-x_3) - (x_1 - x_3)(y-y_3)

外積の性質により、ベクトルの位置を判別できます。

三角形内部の点

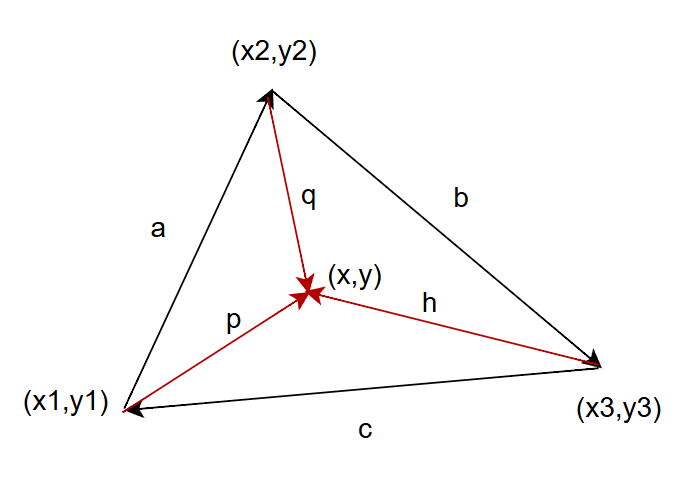
点(x,y)(x,y)が三角形内部にある時、三つの外積の符号が同じです。

三角形外部の点

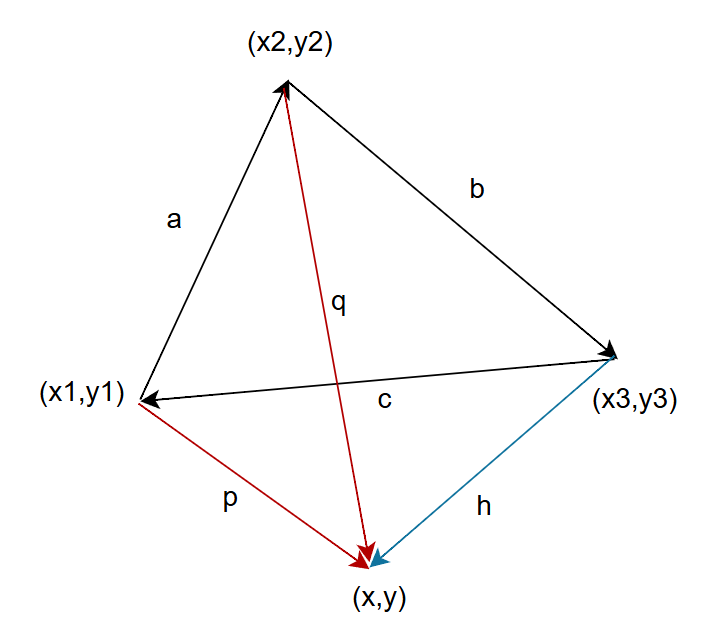
点(x,y)(x,y)が三角形外部にある時、三つの外積の符号が同じではありません。

三角形と点の位置関係

一般化された式​

外積の式をそれぞれ整理した一般化の式：

  • L1=(y2−y1)x+(x1−x2)y+(x2y1−x1y2)L_1 = (y_2 - y_1)x + (x_1 - x_2)y + (x_2 y_1 - x_1 y_2)
  • L2=(y3−y2)x+(x2−x3)y+(x3y2−x2y3)L_2 = (y_3 - y_2)x + (x_2 - x_3)y + (x_3 y_2 - x_2 y_3)
  • L3=(y1−y3)x+(x3−x1)y+(x1y3−x3y1)L_3 = (y_1 - y_3)x + (x_3 - x_1)y + (x_1 y_3 - x_3 y_1)

これらの値 L1,L2,L3L_1, L_2, L_3 の符号が全て正または全て負であれば、点 (x,y)(x,y) は三角形の内部にあります。一方、符号が混在している場合、点は三角形の外部にあります。

C言語での実装​

int isInsideTriangle(int x, int y, int x1, int y1, int x2, int y2, int x3, int y3)
{
    // 外積を計算
    float L1 = (y2 - y1) * x + (x1 - x2) * y + (x2 * y1 - x1 * y2);
    float L2 = (y3 - y2) * x + (x2 - x3) * y + (x3 * y2 - x2 * y3);
    float L3 = (y1 - y3) * x + (x3 - x1) * y + (x1 * y3 - x3 * y1);

    // 点が全ての直線の同じ側にあるかどうかをチェック
    return (L1 >= 0 && L2 >= 0 && L3 >= 0) || (L1 <= 0 && L2 <= 0 && L3 <= 0);
}
使用例
// 三角形の頂点
int x1 = 0, y1 = 0;
int x2 = 5, y2 = 0;
int x3 = 2, y3 = 5;

// 判定したい点
int px = 2, py = 2;

if (isInsideTriangle(px, py, x1, y1, x2, y2, x3, y3)) {
    printf("点(%d, %d)は三角形の内部にあります\n", px, py);
} else {
    printf("点(%d, %d)は三角形の外部にあります\n", px, py);
}

アルゴリズムの特徴​

利点​

  • 計算効率: O(1)の時間計算量で判定可能
  • 数値的安定性: 浮動小数点演算で正確な結果が得られる
  • 実装の簡単さ: 少ない行数で実装できる

注意点​

  • 三角形の頂点が時計回りか反時計回りかによって符号が変わる
  • 境界上の点の扱いについては >= や > の選択に注意が必要
  • 極端に細い三角形では数値誤差の影響を受ける可能性がある

応用例​

このアルゴリズムは以下のような場面で活用されます：

  • コンピュータグラフィックス: レイトレーシングや衝突判定
  • 画像処理: 三角形領域のマスク処理や塗りつぶし
  • ゲーム開発: キャラクターの当たり判定や移動可能領域の判定
  • GIS: 地理情報システムでの領域内判定
性能改善のヒント

大量の点を判定する場合は、事前に三角形の境界ボックス（AABB）をチェックして、明らかに外部にある点を早期に除外することで処理速度を向上させることができます。