線形回帰モデルにおける最小二乗法 (Least Squares Method in Multiple Linear Regression)

最小二乗法は統計学と機械学習における基本的な回帰手法です。この記事では、多項式回帰と正則化最小二乗法について、実際のGDPと乳児死亡率データを用いて詳しく解説します。

ライブラリのインポート

import numpy as np
import scipy as sp
import pandas as pd
from pandas import Series, DataFrame
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns
%matplotlib inline

# 小数第3位まで表示
%precision 3

# ランダムシードの固定
np.random.seed(0)

データセットの準備

今回使用するデータは各国のGDPと乳児死亡率の関係を示すデータセットです。

from google.colab import drive
drive.mount('/content/drive/')

# Read the CSV file from Google Drive, and the data is from course
filename = '/content/drive/My Drive/GDP.csv'

df = pd.read_csv(filename)

# Print the DataFrame
print(df)

データセットの概要：

特徴量: 乳児死亡率 (infant mortality)
目的変数: GDP (Gross Domestic Product)
サンプル数: 193か国

データの可視化

全体のデータ分布

# get mortality
x = np.array(df.iloc[:, 1])
# get gdp
y = np.array(df.iloc[:, 2])

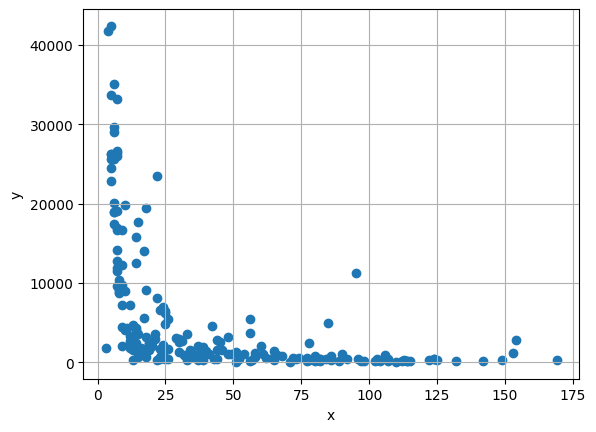
plt.scatter(x, y)
plt.xlabel('Infant Mortality Rate')
plt.ylabel('GDP')
plt.title('GDP vs Infant Mortality Rate')
plt.grid(True)

全データの散布図

データ分割

機械学習の標準的な手法として、データを訓練用と検証用に分割します。

# Split the data for train and test
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, train_size=0.5, test_size=0.5, random_state=0)

# Train data
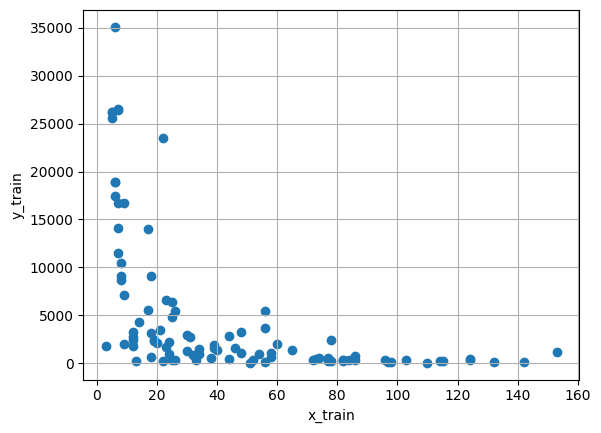
plt.scatter(x_train, y_train)
plt.xlabel('x_train')
plt.ylabel('y_train')
plt.title('Training Data')
plt.grid(True)

訓練データ

# Test data
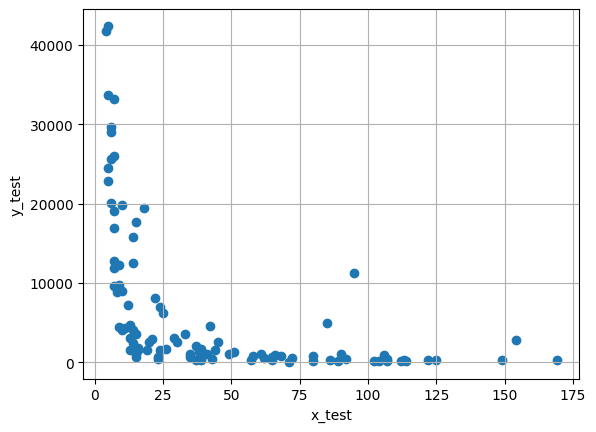
plt.scatter(x_test, y_test)
plt.xlabel('x_test')
plt.ylabel('y_test')
plt.title('Test Data')
plt.grid(True)

検証データ

理論的背景

線形回帰モデル

回帰モデルは以下のように表現されます：

$y=\theta_0+\theta_1\phi_1(x)+\cdots+\theta_{N-1}\phi_{N-1}(x)$

最小二乗推定

パラメータの推定値は以下の公式で求められます：

$\hat{\boldsymbol{\theta}}=(\boldsymbol{H}^T\boldsymbol{H})^{-1} \boldsymbol{H}^T\boldsymbol{y}$

ここで、

\begin{aligned} \boldsymbol{H}&=\begin{bmatrix} 1&\phi_1(x_1)&\cdots&\phi_{N-1}(x_1)\\ 1&\phi_1(x_2)&\cdots&\phi_{N-1}(x_2)\\ \vdots&\vdots&\ddots&\vdots\\ 1&\phi_1(x_M)&\cdots&\phi_{N-1}(x_M) \end{bmatrix}\\ \boldsymbol{y}&=\begin{bmatrix}y_1\\y_2\\\vdots\\y_M\end{bmatrix} \end{aligned}

正則化最小二乗法

過学習を防ぐために、正則化項を追加します：

$\hat{\boldsymbol{\theta}}=(\boldsymbol{H}^T\boldsymbol{H}+\xi\boldsymbol{I})^{-1} \boldsymbol{H}^T\boldsymbol{y}$

ここで、 $\xi$ は正則化定数、 $\boldsymbol{I}$ は単位行列です。

実装

正則化最小二乗法の関数実装

$\phi_k(x)=x^k$ として、正則化最小二乗法による推定を行います。

# 正則化最小二乗法で解を求める rmls(学習データ(x), 学習データ(y), 解空間の次元数N, 正規化定数ξ)
def rmls(x_train, y_train, N, gzai):
    # 行列Hの行数設定
    M = x_train.shape[0]
    
    # xとyをM行1列に変換
    x_train = x_train.reshape((M, 1))
    y_train = y_train.reshape((M, 1))
    
    # 全ての要素が1の列ベクトルを生成
    i = np.ones((M, 1))
    
    H = i
    for k in range(1, N):
        H = np.hstack((H, x_train**(k)))
    
    A = np.dot(H.T, H) + gzai * np.eye(N)
    B = np.dot(H.T, y_train)
    
    # パラメータΘの最小二乗推定値
    lss_c = np.dot(np.linalg.inv(A), B)
    
    # lss_cの要素を逆順に並び替え（多項式係数の順序に合わせる）
    lss_c = np.sort(lss_c)[::-1]
    
    return (lss_c, M)

モデル選択

次数の選択

正則化定数を $\xi = 0.0$ として、最適な多項式の次数を決定します。

# 正則化定数 0.0
# 学習データと検証データでの平均二乗誤差（MSE)の表示
from sklearn.metrics import mean_squared_error
result = []

for N in range(2, 11):
    lss_c, M = rmls(x_train, y_train, N, 0.0)
    
    # 学習データを用いてyを推定
    ys_train = np.polyval(lss_c, x_train)
    
    # 検証データを用いてyを推定
    ys_test = np.polyval(lss_c, x_test)
    
    # 学習データに対するyの推定値の平均二乗誤差
    train_error = mean_squared_error(y_train, ys_train)
    
    # 検証データに対するyの推定値の平均二乗誤差
    test_error = mean_squared_error(y_test, ys_test)
    
    result.append([train_error, test_error])

diff = DataFrame(data=result, columns=['Training', 'Test'], index=[n for n in range(2, 11)])

diff.plot(title='Mean Squared Error vs Polynomial Degree')
plt.xlabel('Polynomial Degree (N)')
plt.ylabel('MSE')
plt.grid(True)

次数選択

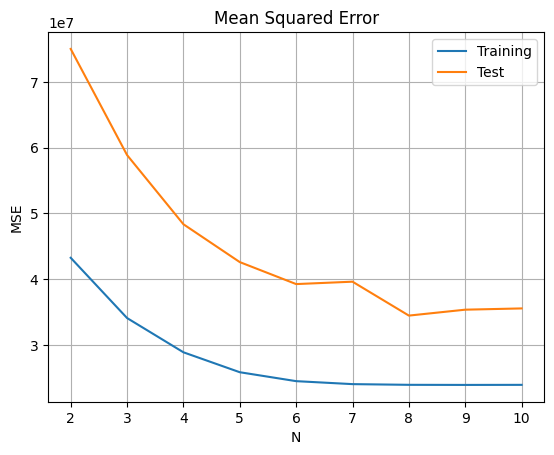
分析結果

正則化定数を $\xi = 0.0$ とした場合、学習データと検証データでの平均二乗誤差（MSE）により、 $N = 8$ の時に最も良い結果が得られます。

正則化定数の選択

次数を $N = 8$ に固定して、最適な正則化定数を決定します。

# 正則化定数の選択
# 学習データと検証データでの平均二乗誤差（MSE)の表示
from sklearn.metrics import mean_squared_error
result = []
N = 8

for gzai in range(0, 10):
    lss_c, M = rmls(x_train, y_train, N, gzai)
    
    # 学習データを用いてyを推定
    ys_train = np.polyval(lss_c, x_train)
    
    # 検証データを用いてyを推定
    ys_test = np.polyval(lss_c, x_test)
    
    # 学習データに対するyの推定値の平均二乗誤差
    train_error = mean_squared_error(y_train, ys_train)
    
    # 検証データに対するyの推定値の平均二乗誤差
    test_error = mean_squared_error(y_test, ys_test)
    
    result.append([train_error, test_error])

diff = DataFrame(data=result, columns=['Training', 'Test'], index=[n for n in range(0, 10)])

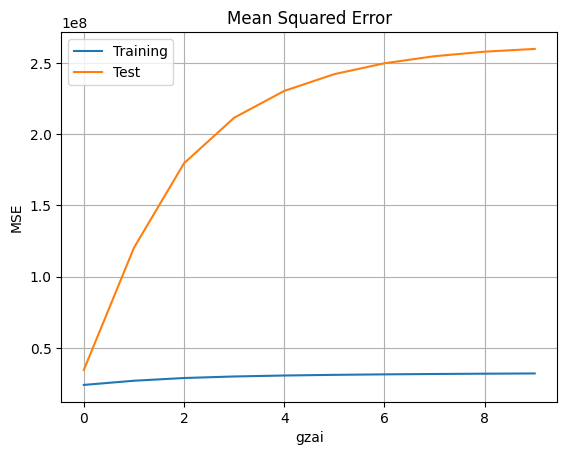
diff.plot(title='Mean Squared Error vs Regularization Parameter')
plt.xlabel('Regularization Parameter (ξ)')
plt.ylabel('MSE')
plt.grid(True)

正則化定数選択

分析結果

回帰次数が $N = 8$ とした場合、学習データと検証データでの平均二乗誤差（MSE）により、正則化定数が $\xi = 0.0$ の時に最も良い結果が得られます。正則化定数が大きくなると、モデルの複雑性が制限され、場合によっては学習不足（underfitting）になる可能性があります。

最終モデルの可視化

正則化パラメータの影響

# 回帰次数
N = 8

# データプロット
plt.scatter(x_train, y_train, label='Training Data', alpha=0.6)

# 正則化パラメタのリスト
gzai = np.array([0, 0.1, 1, 10])

# プロットのラインスタイル
ls = ['-', '--', '-.', ':']

# 正則化最小二乗法による推定
for i in np.arange(gzai.size):
    lss_c, M = rmls(x_train, y_train, N, gzai[i])
    xs = np.linspace(np.min(x_train), np.max(x_train), M)
    ys = np.polyval(lss_c, xs)
    plt.plot(xs, ys, label='ξ='+str(round(gzai[i], 3)), ls=ls[i], lw=2)

# 結果の表示
plt.title('Regularized Least Squares (N = %d)' % (N))
plt.xlabel('Infant Mortality Rate')
plt.ylabel('GDP')
plt.legend(loc='best', frameon=False)
plt.grid(True)

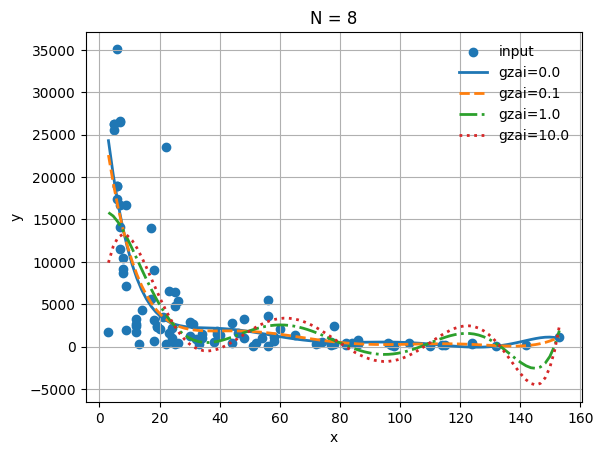
最終モデル

最適モデルのパラメータ

# 推定パラメータ
print("最適モデルのパラメータ:")
print(lss_c)

最も良い回帰モデル（ $N = 8$ , $\xi = 0.0$ ）：

\begin{aligned} y &= 1.430 \times 10^{-8}x^8 - 7.813 \times 10^{-6}x^7 + 1.692 \times 10^{-3}x^6\\ &\quad - 1.841 \times 10^{-1}x^5 + 1.048 \times 10^{1}x^4 - 2.911 \times 10^{2}x^3\\ &\quad + 2.971 \times 10^{3}x^2 + 3.486 \times 10^{3}x + \theta_0 \end{aligned}

結論と考察

主要な発見

最適な多項式次数: $N = 8$ が訓練データと検証データの両方で最良の性能を示した
正則化の効果: この問題では $\xi = 0.0$ が最適だったが、これはデータの性質とサンプル数に依存
非線形関係: GDPと乳児死亡率の間には明確な非線形関係が存在する

実用的な意義

この分析から以下の洞察が得られます：

経済発展と健康指標: 経済発展（GDP）と健康指標（乳児死亡率）の間には強い相関関係がある
政策立案: この関係性は公衆衛生政策や経済政策の立案に有用な情報を提供する
予測モデル: 構築したモデルは他国の状況予測や政策効果の推定に活用可能

手法の特徴

最小二乗法の利点

解析的解: 閉形式の解が存在するため計算が高速
理論的基盤: 統計学的に確立された手法
解釈可能性: パラメータの意味が明確

正則化の重要性

過学習の防止: 高次多項式でも汎化性能を維持
数値安定性: 行列の条件数改善による安定した計算
特徴選択: L2正則化により不要な特徴の影響を抑制

改善点と発展

交差検証: より robust なモデル選択のためのk-fold交差検証
他の正則化手法: L1正則化（Lasso）やElastic Netの適用
非線形変換: 対数変換などによるデータの前処理
外れ値処理: Robust回帰手法の適用

実践的なアドバイス

モデル選択: 常に訓練誤差と検証誤差の両方を監視する
正則化: データ量が少ない場合や高次元問題では正則化が特に重要
解釈: 高次多項式は予測性能は良いが、解釈が困難になる場合がある

注意点

外挿の危険性: 訓練データの範囲外での予測は信頼性が低い
因果関係: 相関関係があっても因果関係があるとは限らない
モデルの前提: 線形回帰の前提条件（独立性、等分散性など）の確認が重要

次のステップ

さらなる学習のための推奨項目：

他の回帰手法: Ridge回帰、Lasso回帰、ランダムフォレスト
モデル診断: 残差分析、影響度診断
ベイズ線形回帰: 不確実性の定量化
一般化線形モデル: ロジスティック回帰、ポアソン回帰

ライブラリのインポート​

データセットの準備​

データの可視化​

全体のデータ分布​

データ分割​

理論的背景​

線形回帰モデル​

最小二乗推定​

正則化最小二乗法​

実装​

正則化最小二乗法の関数実装​

モデル選択​

次数の選択​

正則化定数の選択​

最終モデルの可視化​

正則化パラメータの影響​

最適モデルのパラメータ​

結論と考察​

主要な発見​

実用的な意義​

手法の特徴​

最小二乗法の利点​

正則化の重要性​

改善点と発展​

次のステップ​