Optimal Control Problem Formulation
This document introduces the fundamental concepts of optimal control problems using the unicycle model as a practical example. We explore different control objectives from basic parking problems to advanced collision avoidance scenarios.
Unicycle Model
The unicycle model serves as an excellent example for understanding nonlinear optimal control problems due to its simplicity and practical relevance in robotics.
State Space Representation
The state vector is defined as:
Where:
- : position in x direction
- : position in y direction
- : linear velocity
- : wheel orientation angle
Control Input
The control input vector is:
Where:
- : linear acceleration
- : angular velocity
Continuous-Time Dynamics
The state equation for the unicycle model is:
This is a nonlinear system due to the trigonometric functions in the kinematic equations.
Discretization
For numerical implementation, we discretize the system with sample time :
where represents the discrete-time dynamics obtained through numerical integration methods.
Problem 1: Parking Problem
The parking problem represents the most basic optimal control scenario - moving from an initial state to a desired final state.
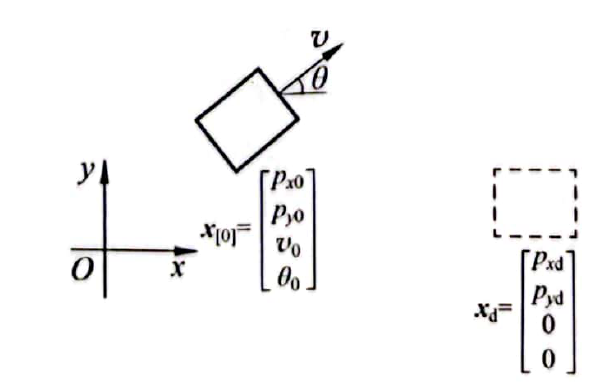
Problem Setup
System: Discrete-time unicycle model
Initial and target states:
Terminal state: At time :
The final state depends only on the initial state and the sequence of control inputs .
Performance Function
The basic performance function (cost function) is:
where is the error vector.
Control Policy
The optimal control policy seeks:
where is the set of admissible controls.
Weight Matrix
To prioritize certain states, we introduce a weight matrix:
where is a positive semi-definite symmetric matrix ( and ).
- Usually diagonal: for
- Larger diagonal elements indicate higher importance of corresponding states
- Must be positive semi-definite for convexity
Constraints
Physical limitations impose constraints:
State constraints:
Input constraints:
These are hard constraints that must be strictly satisfied during system operation.
Problem 2: Input Cost Consideration
Real systems require energy to operate, making input cost an important consideration.
Soft Constraints
Unlike hard constraints, soft constraints aren't strictly enforced but are penalized in the cost function.
Modified Cost Function
Where:
- : terminal cost
- : input cost
- : reference weight matrix
- : input cost weight matrix
Design Trade-offs
The relative weighting determines system behavior:
: Control performance is more important!
: Input cost is more important!
Problem 3: Trajectory Tracking
Moving beyond point-to-point control, trajectory tracking follows a time-varying reference.
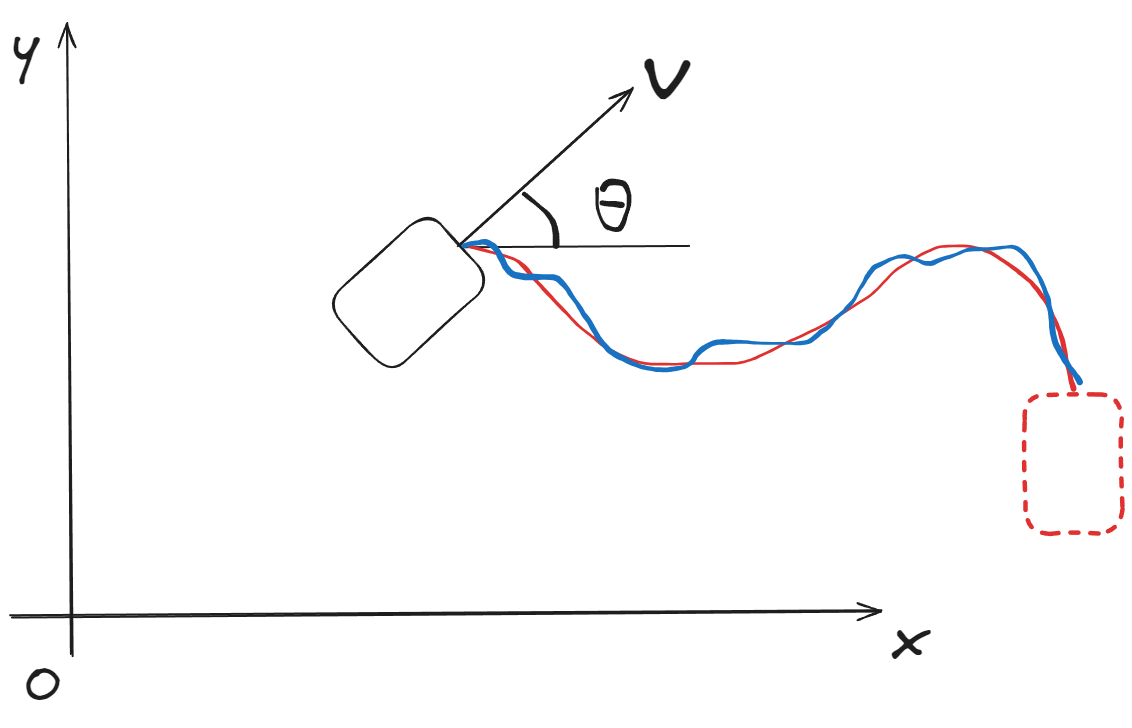
Reference Trajectory
Performance Function
where is the trajectory weight matrix that penalizes deviations from the reference path at each time step.
Problem 4: Collision Avoidance
Advanced control problems must consider safety and obstacle avoidance.
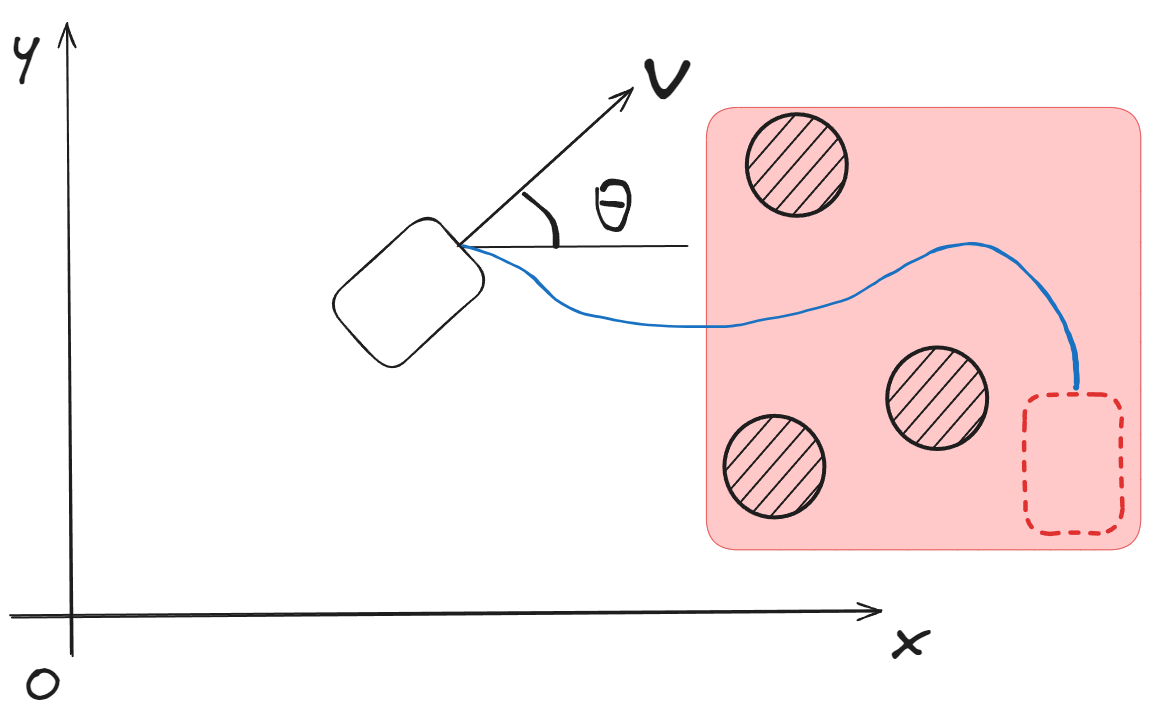
Method 1: Hard Constraint Approach
Add constraint conditions to Problem 3:
where represents the obstacle space.
Method 2: Soft Constraint Approach
Modify the cost function to penalize proximity to obstacles:
Where:
- : distance from object to obstacle at time
- : weight matrix for distance penalty
- : penalty that increases as distance decreases
General Optimal Control Problem Formulation
System Model
Reference
Performance Function
Constraints
- State constraints: (admissible trajectory set)
- Input constraints: (admissible control set)
There must be at least one feasible solution within the constraints. Overly restrictive constraints can lead to infeasible problems.
Common Optimal Control Problem Types
1. Minimum Time Problem
Objective: Reach the target in minimum time.
2. Terminal Control Problem
Objective: Minimize final state error.
3. Minimum Input Problem
Objective: Minimize control effort.
4. Trajectory Tracking Problem
Objective: Follow reference trajectory closely.
5. General Optimal Control Problem
Objective: Balance terminal accuracy, trajectory tracking, and input cost.
6. Regulator Problem
When , the problem becomes a regulator problem:
For trajectory problems, introduce error and formulate the error dynamics. The control task becomes driving , which can be solved as a regulator problem.
Solution Approaches
Different optimal control problems require different solution methods:
- Linear Quadratic Regulator (LQR): For linear systems with quadratic costs
- Dynamic Programming: For general nonlinear problems
- Model Predictive Control (MPC): For real-time implementation with constraints
- Pontryagin's Maximum Principle: For continuous-time problems
- Direct Methods: Numerical optimization of discretized problems
References
- Optimal Control by DR_CAN
- Wang, T. (2023). 控制之美 (卷2). Tsinghua University Press.
- Grüne, L., & Pannek, J. (2017). Nonlinear Model Predictive Control. Springer.
- Kirk, D. E. (2004). Optimal Control Theory: An Introduction. Dover Publications.
