跳到主要内容

ラプラス変換

ラプラス変換は、フーリエ変換を発散しやすい信号にも適用できるよう拡張した変換手法です。特に制御工学や微分方程式の解法において極めて重要な役割を果たします。

フーリエ変換からラプラス変換へ​

存在条件の問題​

フーリエ変換が存在するためには、以下の条件が必要です：

∫−∞∞∣f(t)∣dt<∞\int_{-\infty}^{\infty} |f(t)|dt < \infty

しかし、実際の信号には以下のような分類があります：

  • 瞬時波：絶対可積分であり、フーリエ変換が存在する
  • 持続波：絶対可積分ではなく、フーリエ変換が存在しない（積分が発散）
フーリエ変換の限界

フーリエ変換は絶対可積分とは限らない信号に対して、積分が発散する可能性があります。これは多くの実用的な信号で問題となります。

収束因子の導入​

ラプラス変換では、s=σ+jωs = \sigma + j\omega における収束因子 e−σte^{-\sigma t} を導入することで、発散する信号も収束させることができます。

f(t)e−atf(t)e^{-at} （a>0a > 0）とすることで、信号を絶対可積分にできます：

F(ω)=∫−∞∞[f(t)e−at]e−jωtdtF(\omega) = \int_{-\infty}^{\infty} [f(t)e^{-at}]e^{-j\omega t}dt

a+jω→sa + j\omega \to s と置き換えることで、ラプラス変換が導かれます。

因果律による制約​

制御工学では因果律により、x(t)x(t)（t≥0t \geq 0）について考える必要があります。

フーリエ変換： X(ω)=∫0∞x(t)e−jωtdtX(\omega) = \int_{0}^{\infty} x(t)e^{-j\omega t}dt

これが発散する場合、収束させるために： ∫0∞[x(t)e−at]e−jωtdt=∫0∞x(t)e−(a+jω)tdt\int_{0}^{\infty} [x(t)e^{-at}] e^{-j\omega t}dt = \int_{0}^{\infty} x(t)e^{-(a+j\omega) t}dt

ラプラス変換の定義​

基本定義​

ラプラス変換：

X(s)=∫0∞x(t)e−stdtX(s) = \int_{0}^{\infty} x(t)e^{-st}dt

ここで s=σ+jωs = \sigma + j\omega は複素変数です。

逆ラプラス変換​

逆ラプラス変換：

x(t)=12πj∫a−j∞a+j∞X(s)estdsx(t) = \frac{1}{2\pi j}\int_{a-j\infty}^{a+j\infty} X(s)e^{st}ds

実際には、部分分数展開（ヘビサイドの展開定理）によってラプラス変換表を使用するのが一般的です。

実用的な逆変換

逆ラプラス変換を直接計算することは稀であり、通常は部分分数展開とラプラス変換表を用いて求めます。

畳み込み定理​

フーリエ変換と同様に、ラプラス変換でも畳み込み定理が成り立ちます：

L[f(t)∗g(t)]=L[f(t)]⋅L[g(t)]\mathcal{L}[f(t) * g(t)] = \mathcal{L}[f(t)] \cdot \mathcal{L}[g(t)]

ここで L[f(t)]\mathcal{L}[f(t)] は関数 f(t)f(t) のラプラス変換です。

この定理により：

  • 時間領域での畳み込み演算が周波数領域での掛け算に変換される
  • 微分方程式の解法が代数方程式に変換される
  • 高速フーリエ変換（FFT）を用いた高速計算が可能
計算の効率化

実際の計算では、関数 f,gf, g の高速フーリエ変換（FFT）を掛け算した結果を逆高速フーリエ変換（IFFT）することで、高速に畳み込み計算を処理するのが一般的です。

ラプラス変換の性質​

ラプラス変換は多くの有用な性質を持ちます：

線形性​

L[af(t)+bg(t)]=aL[f(t)]+bL[g(t)]\mathcal{L}[af(t) + bg(t)] = a\mathcal{L}[f(t)] + b\mathcal{L}[g(t)]

時間軸の移動​

L[f(t−a)u(t−a)]=e−asF(s)\mathcal{L}[f(t-a)u(t-a)] = e^{-as}F(s)

ここで u(t)u(t) は単位ステップ関数です。

減衰性（周波数軸の移動）​

L[e−atf(t)]=F(s+a)\mathcal{L}[e^{-at}f(t)] = F(s+a)

相似性（スケーリング）​

L[f(at)]=1aF(sa)\mathcal{L}[f(at)] = \frac{1}{a}F\left(\frac{s}{a}\right)

微分の性質​

L[df(t)dt]=sF(s)−f(0−)\mathcal{L}\left[\frac{df(t)}{dt}\right] = sF(s) - f(0^-)

L[d2f(t)dt2]=s2F(s)−sf(0−)−f′(0−)\mathcal{L}\left[\frac{d^2f(t)}{dt^2}\right] = s^2F(s) - sf(0^-) - f'(0^-)

積分の性質​

L[∫0tf(τ)dτ]=F(s)s\mathcal{L}\left[\int_{0}^{t} f(\tau)d\tau\right] = \frac{F(s)}{s}

初期値定理​

lim⁡t→0+f(t)=lim⁡s→∞sF(s)\lim_{t \to 0^+} f(t) = \lim_{s \to \infty} sF(s)

最終値定理​

lim⁡t→∞f(t)=lim⁡s→0sF(s)\lim_{t \to \infty} f(t) = \lim_{s \to 0} sF(s)

（sF(s)sF(s) の極がすべて左半平面にある場合）

ラプラス変換表​

主要な関数のラプラス変換：

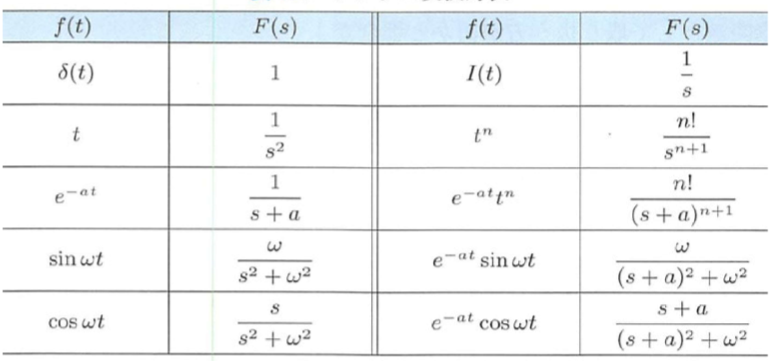
ラプラス変換表

基本的なラプラス変換対​

時間関数 f(t)f(t)ラプラス変換 F(s)F(s)
δ(t)\delta(t)11
u(t)u(t)1s\frac{1}{s}
tt1s2\frac{1}{s^2}
tnt^nn!sn+1\frac{n!}{s^{n+1}}
e−ate^{-at}1s+a\frac{1}{s+a}
sin⁡(ωt)\sin(\omega t)ωs2+ω2\frac{\omega}{s^2+\omega^2}
cos⁡(ωt)\cos(\omega t)ss2+ω2\frac{s}{s^2+\omega^2}
e−atsin⁡(ωt)e^{-at}\sin(\omega t)ω(s+a)2+ω2\frac{\omega}{(s+a)^2+\omega^2}
e−atcos⁡(ωt)e^{-at}\cos(\omega t)s+a(s+a)2+ω2\frac{s+a}{(s+a)^2+\omega^2}

制御工学での応用​

伝達関数​

ラプラス変換により、線形時不変システムの入出力関係を伝達関数で表現できます：

G(s)=Y(s)X(s)G(s) = \frac{Y(s)}{X(s)}

安定性解析​

  • 極の位置：システムの安定性は伝達関数の極の位置で決まる
  • 左半平面：安定
  • 右半平面：不安定

制御系設計​

  • PID制御器：Gc(s)=Kp+Kis+KdsG_c(s) = K_p + \frac{K_i}{s} + K_d s
  • 補償器設計：根軌跡法、周波数応答法
  • フィードバック解析：閉ループ安定性の解析

まとめ​

ラプラス変換は制御工学と信号処理の基礎となる重要なツールです：

  1. 拡張性：フーリエ変換では扱えない発散信号も処理可能
  2. 微分方程式の解法：代数方程式への変換により解法が簡単化
  3. システム解析：伝達関数による線形システムの解析
  4. 制御系設計：安定性解析と補償器設計の基礎

次章では、離散時間システムで使用されるZ変換について学習します。

次のステップ
  • Z変換：離散時間システムのためのラプラス変換
  • 伝達関数：制御系の数学的表現
  • 安定性理論：システムの安定性判別法
  • 制御系設計：PID制御とその他の制御手法