跳到主要内容

フィルタ設計の基礎

信号処理におけるフィルタとは、信号の周波数特性を操作するものであり、信号の不要な周波数成分を除去したり減衰させたりして、必要な周波数成分のみからなる信号を得る処理を行うものです。

フィルタの種類​

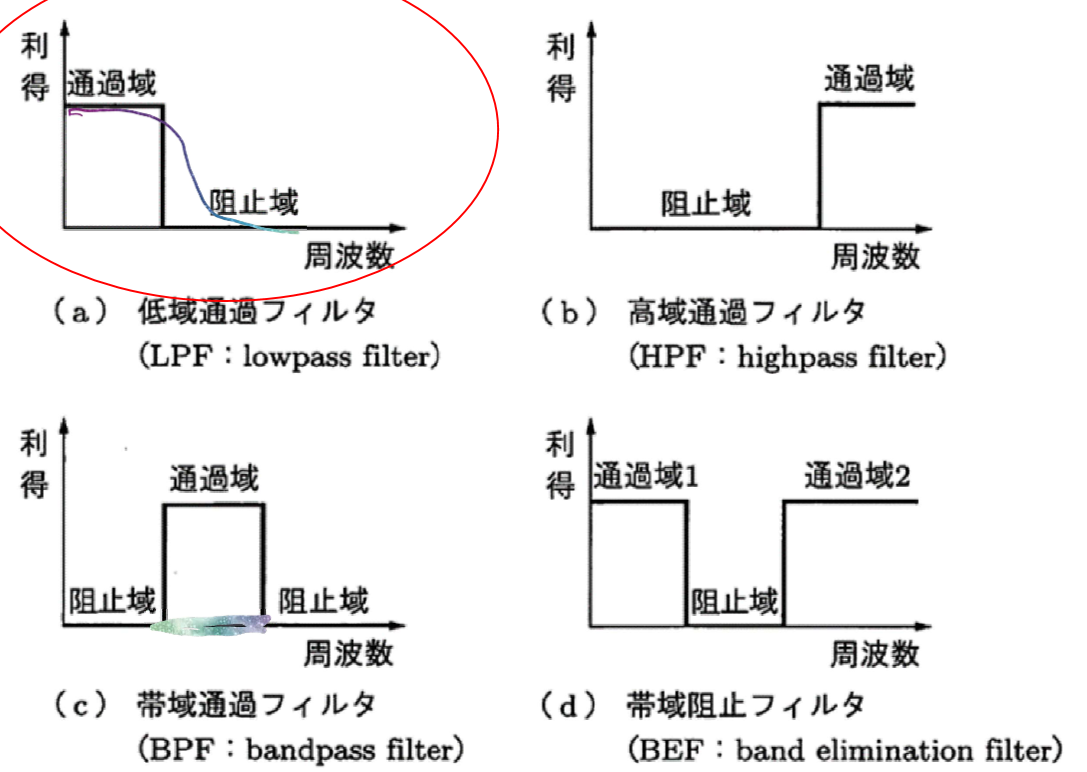
基本的なフィルタタイプ​

フィルタの種類

  1. LPF（Low-Pass Filter、低域通過フィルタ）

    • 低い周波数成分を通し、高い周波数成分を遮断
    • 用途：ノイズ除去、アンチエイリアシング

  2. HPF（High-Pass Filter、高域通過フィルタ）

    • 高い周波数成分を通し、低い周波数成分を遮断
    • 用途：DC成分除去、高周波ノイズ強調

  3. BPF（Band-Pass Filter、帯域通過フィルタ）

    • 特定の周波数帯域のみを通す
    • 用途：特定周波数成分の抽出、通信システム

  4. BEF（Band-Elimination Filter、帯域阻止フィルタ）

    • 特定の周波数帯域を遮断
    • 用途：ノッチフィルタ、電源周波数ノイズ除去

理想的なフィルタの条件​

理想的なフィルタは以下の特性を満たします：

  1. 通過域で利得（ゲイン）が一定
  2. 過渡域での傾きが急峻
  3. 阻止域の利得が0
  4. 直線位相特性（通過域で位相特性が周波数に比例して直線的に変化）
理想と現実

実際のフィルタでは、これらすべての条件を同時に満たすことは不可能であり、用途に応じて最適化する特性を選択する必要があります。

アナログフィルタ設計​

フィルタ設計のステップ​

  1. フィルタの近似：所望の特性をもつ伝達関数を設計
  2. 回路実現：求められた伝達関数を抵抗、コンデンサ、コイル、オペアンプなどの素子を用いて回路として実現
設計の基本方針

フィルタの設計は**LPF（低域通過フィルタ）**が基本となっており、他のフィルタタイプは周波数変換により実現されます。

代表的なフィルタ​

  1. 一次遅れ系によるフィルタ
  2. バターワースフィルタ（Butterworth filter）
  3. チェビシェフフィルタ（Chebyshev filter）

バターワースフィルタ​

バターワースフィルタは、通過域で最も平坦な周波数特性を持つフィルタとして知られています。

周波数特性の定義​

まず、周波数特性 ∣H(ω)∣2|H(\omega)|^2 を決定します（次数 NN、遮断周波数 ωc\omega_c）：

バターワースフィルタの周波数特性： ∣H(ω)∣2=11+(ω/ωc)2N|H(\omega)|^2 = \frac{1}{1+(\omega/\omega_c)^{2N}}

伝達関数の導出​

連続時間伝達関数の絶対値の2乗 ∣H(s)∣2|H(s)|^2 を得るために、s=jωs = j\omega を代入します：

∣H(s)∣2=∣H(ω)∣ω=s/j2=11+(−j)2N(s/ωc)2N|H(s)|^2 = |H(\omega)|^2_{\omega=s/j} = \frac{1}{1+(-j)^{2N}(s/\omega_c)^{2N}}

=11+(−1)2N(j2)N(s/ωc)2N=11+(−1)N(s/ωc)2N= \frac{1}{1+(-1)^{2N}(j^2)^N(s/\omega_c)^{2N}} = \frac{1}{1+(-1)^N(s/\omega_c)^{2N}}

極の計算​

フィルタの極を求めるために、分母 = 0 とします：

(−1)N(s/ωc)2N=−1(-1)^N(s/\omega_c)^{2N} = -1

複素数のn乗根

複素数 w=R(cos⁡α+jsin⁡α)w = R(\cos\alpha + j\sin\alpha) に対して： s=r(cos⁡θ+jsin⁡θ)s = r(\cos\theta + j\sin\theta) sn=rn(cos⁡nθ+jsin⁡nθ)=R(cos⁡α+jsin⁡α)s^n = r^n(\cos{n\theta} + j\sin{n\theta}) = R(\cos\alpha + j\sin\alpha)

したがって：

  • r=R1/nr = R^{1/n}
  • nθ=α+2πkn\theta = \alpha + 2\pi k, (k=0,1,…,n−1)(k = 0,1,\ldots,n-1)

n個の根が存在します。

N が偶数の場合​

(sωc)2N=−1=ej(π+2kπ)\left(\frac{s}{\omega_c}\right)^{2N} = -1 = e^{j(\pi+2k\pi)}

s2N=ωc2Nej(π+2kπ),k=0,1,…,2N−1s^{2N} = \omega_c^{2N}e^{j(\pi+2k\pi)}, \quad k = 0,1,\ldots,2N-1

したがって、2N2N 個の根：

sk=ωc⋅ej(π+2kπ)2N,k=0,1,…,2N−1s_k = \omega_c \cdot e^{\frac{j(\pi+2k\pi)}{2N}}, \quad k = 0,1,\ldots,2N-1

N が奇数の場合​

(sωc)2N=1=ej(0+2kπ)\left(\frac{s}{\omega_c}\right)^{2N} = 1 = e^{j(0+2k\pi)}

s2N=ωc2Nej(2kπ),k=0,1,…,2N−1s^{2N} = \omega_c^{2N}e^{j(2k\pi)}, \quad k = 0,1,\ldots,2N-1

したがって、2N2N 個の根：

sk=ωc⋅ejkπN,k=0,1,…,2N−1s_k = \omega_c \cdot e^{j\frac{k\pi}{N}}, \quad k = 0,1,\ldots,2N-1

伝達関数の構成​

安定な根 sks_k を選択します（実数部が負数）：

H(s)=K(s−si)(s−sj)⋯H(s) = \frac{K}{(s-s_i)(s-s_j)\cdots}

ここで、KK は正規化定数です。

安定性の確保

左半平面（実数部が負）の極のみを選択することで、システムの安定性が保証されます。

周波数変換​

実際にフィルタを設計する際には、LPFを基本として、他のフィルタタイプに変換できます。

遮断周波数の変換（LPF）​

s→sω1s \rightarrow \frac{s}{\omega_1}

通過域：[0,ω1][0, \omega_1]、ω1\omega_1：LPFの遮断周波数

HPFへの変換​

s→ωhss \rightarrow \frac{\omega_h}{s}

通過域：[ωh,∞)[\omega_h, \infty)、ωh\omega_h：HPFの遮断周波数

BPFへの変換​

s→s2+ω1ω2Bωss \rightarrow \frac{s^2 + \omega_1\omega_2}{B_\omega s}

通過域：[ω1,ω2][\omega_1, \omega_2]、BωB_\omega：帯域幅

ここで：

  • ω1,ω2\omega_1, \omega_2：下側・上側遮断周波数
  • Bω=ω2−ω1B_\omega = \omega_2 - \omega_1：帯域幅

BEFへの変換​

s→Bωss2+ω1ω2s \rightarrow \frac{B_\omega s}{s^2 + \omega_1\omega_2}

阻止域：[ω1,ω2][\omega_1, \omega_2]、BωB_\omega：帯域幅

変換の物理的意味

これらの変換は、複素周波数平面上での幾何学的変換に対応しており、元のLPFの特性を保持しながら所望の周波数特性を実現します。

フィルタ設計の実際​

設計パラメータ​

  1. 遮断周波数：ωc\omega_c
  2. 次数：NN（急峻性とリップルのトレードオフ）
  3. 通過域リップル：許容できる変動
  4. 阻止域減衰量：必要な減衰レベル

性能評価指標​

  • 通過域リップル：通過域での利得変動
  • 阻止域減衰量：不要信号の抑圧レベル
  • 過渡域幅：通過域から阻止域への遷移幅
  • 群遅延特性：位相歪みの評価

まとめ​

フィルタ設計は信号処理において基礎的かつ重要な技術です：

  1. 基本理解：各フィルタタイプの特性と用途
  2. 設計理論：バターワースフィルタを例とした数学的設計手法
  3. 周波数変換：LPFから他のフィルタタイプへの変換技術
  4. 実用性：設計パラメータと性能指標の関係

次章では、FIRフィルタとIIRフィルタの具体的な設計手法について詳しく学習します。

次のステップ
  • FIRフィルタ設計：窓関数法と周波数サンプリング法
  • IIRフィルタ設計：双一次変換とインパルス不変変換
  • 適応フィルタ：時変環境での自動調整
  • マルチレートシステム：サンプリングレート変換