正則化ミニマムノルム解 (Regularized Minimal-Norm Solution)

線形回帰において、データの過学習を防ぎ、汎化性能を向上させるための正則化手法について学習します。正則化ミニマムノルム解は、最小二乗解に正則化項を追加することで、モデルの複雑さを制御する重要な手法です。

概要

正則化ミニマムノルム解は以下の最適化問題を解きます：

$\min_{\theta} \|H\theta - y\|^2 + \xi\|\theta\|^2$

ここで：

• $H$：観測行列（設計行列）
• $\theta$：推定すべきパラメータベクトル
• $y$：観測データ
• $\xi$：正則化パラメータ

理論的背景

正則化の必要性

通常の最小二乗法では、観測データに対して完全にフィットするモデルを作成しますが、これは以下の問題を引き起こす可能性があります：

1. 過学習（Overfitting）：訓練データに過度に適応し、新しいデータに対する予測性能が低下
2. 数値的不安定性：観測行列が特異に近い場合の計算の不安定性
3. 高分散：少数のサンプルから高次元のパラメータを推定する際の不確実性

正則化項の効果

正則化項 $\xi\|\theta\|^2$ を追加することで：

• パラメータの大きさを制約し、モデルの複雑さを制御
• 数値的安定性の向上
• バイアス-分散トレードオフの最適化

実装とシミュレーション

必要なライブラリのインポート

import numpy as np
import scipy as sp
import pandas as pd
from pandas import Series, DataFrame
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split

import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns

# 小数第3位まで表示
np.set_printoptions(precision=3)

# ランダムシードの固定
np.random.seed(123)

正則化ミニマムノルム解関数の実装

def lms(x_train, y_train, N, gzai):
    """
    正則化ミニマムノルム解を計算する関数
    
    Parameters:
    -----------
    x_train : array-like
        学習データの入力
    y_train : array-like
        学習データの出力
    N : int
        解空間の次元数（多項式の次数+1）
    gzai : float
        正則化定数（ξ）
    
    Returns:
    --------
    lss_c : ndarray
        正則化最小二乗推定値
    M : int
        観測データ数
    Q : ndarray
        分解能行列
    """
    # 行列Hの行数設定
    M = x_train.shape[0]
    
    # xとyをM行1列に変換
    x_train = x_train.reshape((M, 1))
    y_train = y_train.reshape((M, 1))
    
    # 全ての要素が1の列ベクトルを生成（定数項）
    i = np.ones((M, 1))
    
    # 設計行列Hの構築（多項式基底）
    H = i
    for k in range(1, N):
        H = np.hstack((H, x_train**k))
    
    # 正則化付き正規方程式の解
    # (H^T H + ξI)θ = H^T y
    A = np.dot(H, H.T) + gzai * np.eye(M)
    
    # パラメータΘの正則化最小二乗推定値
    lss_c = np.dot(np.dot(H.T, np.linalg.inv(A)), y_train)
    
    # 分解能行列Qの計算
    Q = np.dot(np.dot(H.T, np.linalg.inv(A)), H)
    
    # lss_cの要素を逆順に並び替え（poly1dとの互換性のため）
    lss_c = np.sort(lss_c.flatten())[::-1]
    
    return (lss_c, M, Q)

数学的詳細

設計行列 $H$ は多項式基底を使用： $H = [1, x, x^2, \ldots, x^{N-1}]$

正則化された正規方程式： $(H^T H + \xi I)\theta = H^T y$

解は： $\theta = (H^T H + \xi I)^{-1} H^T y$

実験1：基本的な関数近似

観測データの生成

設定：

• サンプル数：20（学習・テスト各10）
• 元の関数：$y = \sin(\pi x) - \cos(\pi x), \quad 0 < x < 2$
• ノイズ：平均0、標準偏差0.3の正規分布

x = []
y = []
# サンプル数
sample = 20
# ノイズ標準偏差
sigma = 0.3

# ノイズ（正規分布）
e = np.random.normal(0, sigma, sample)

# 信号生成
x = np.random.uniform(0, 2, sample)
y = np.sin(np.pi*x) - np.cos(np.pi*x) + e

# データを学習用と検証用に分割
x_train, x_test, y_train, y_test = train_test_split(
    x, y, train_size=0.5, test_size=0.5, random_state=0
)

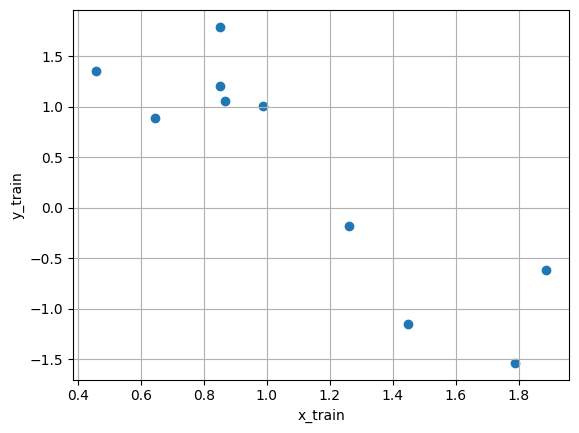
学習データの可視化

plt.figure(figsize=(10, 4))

plt.subplot(1, 2, 1)
plt.scatter(x_train, y_train, alpha=0.7)
plt.xlabel('x_train')
plt.ylabel('y_train')
plt.title('Training Data')
plt.grid(True)

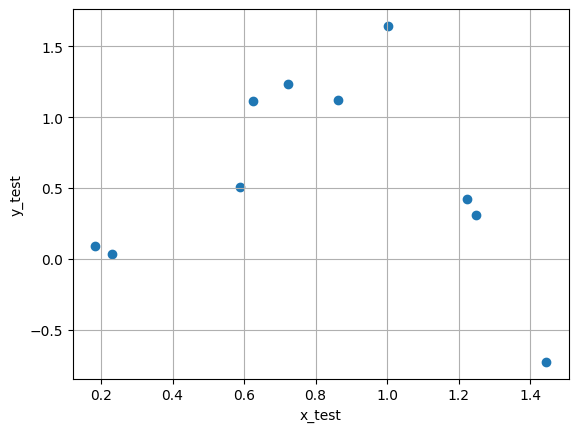
plt.subplot(1, 2, 2)
plt.scatter(x_test, y_test, alpha=0.7)
plt.xlabel('x_test')
plt.ylabel('y_test')
plt.title('Test Data')
plt.grid(True)

plt.tight_layout()
plt.show()

解空間次元Nの影響分析

# 異なるNに対する性能評価
diff = []
result = []

for N in range(2, 30):
    lss_c, M, Q = lms(x_train, y_train, N, 0.1)
    
    # 学習データを用いてyを推定
    ys_train = np.polyval(lss_c, x_train)
    
    # 検証データを用いてyを推定
    ys_test = np.polyval(lss_c, x_test)
    
    # 平均二乗誤差の計算
    train_error = mean_squared_error(y_train, ys_train)
    test_error = mean_squared_error(y_test, ys_test)
    
    result.append([train_error, test_error])

# 結果の可視化
diff = DataFrame(data=result, columns=['Training', 'Test'], 
                index=[n for n in range(2, 30)])

diff.plot(title='Mean Squared Error vs Model Complexity (N)')
plt.xlabel('N (Model Complexity)')
plt.ylabel('MSE')
plt.grid(True)
plt.legend()
plt.show()

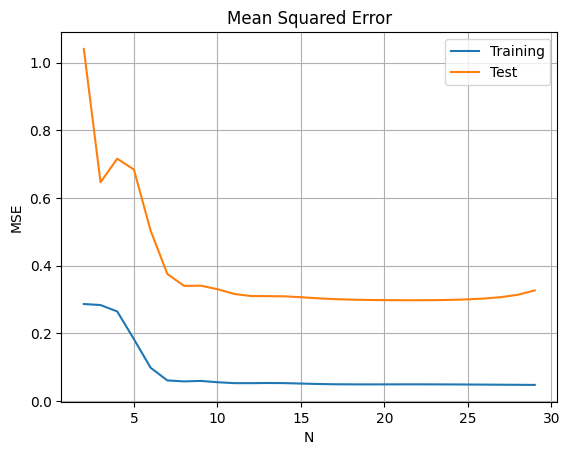
解空間次元の選択

• 低次元（N小）：アンダーフィッティング、バイアスが大きい
• 高次元（N大）：オーバーフィッティング、分散が大きい
• 適切な次元：バイアス-分散トレードオフの最適点

正則化パラメータξの最適化

N = 13
result = []

# 正則化パラメータの範囲を探索
for gzai_i in range(1, 1000):
    gzai = gzai_i * 0.01
    
    lss_c, M, Q = lms(x_train, y_train, N, gzai)
    
    # 予測値の計算
    ys_train = np.polyval(lss_c, x_train)
    ys_test = np.polyval(lss_c, x_test)
    
    # 誤差の計算
    train_error = mean_squared_error(y_train, ys_train)
    test_error = mean_squared_error(y_test, ys_test)
    
    result.append([gzai, train_error, test_error])

# 結果の可視化
diff = DataFrame(data=result, columns=['gzai', 'Training', 'Test'])

diff.plot(x='gzai', y=['Training', 'Test'])
plt.title(f'Mean Squared Error vs Regularization Parameter (σ = {sigma:.3f})')
plt.xlabel('ξ (Regularization Parameter)')
plt.ylabel('MSE')
plt.grid(True)
plt.show()

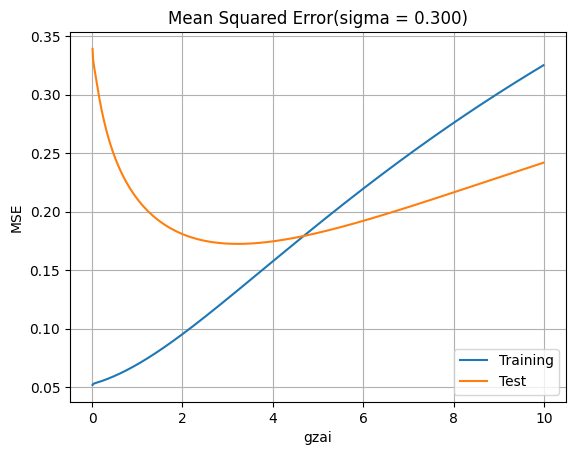
最適パラメータでの結果

N = 13
gzai = 0.32

lss_c, M, Q = lms(x_train, y_train, N, gzai)

# 予測曲線の生成
xs = np.linspace(np.min(x_train), np.max(x_train), M)
ys = np.polyval(lss_c, xs)

# 学習データの予測
ys_train = np.polyval(lss_c, x_train)

# 真の曲線
linex = np.arange(0, 2.0, 0.01)
liney = np.sin(np.pi*linex) - np.cos(np.pi*linex)

# 可視化
plt.figure(figsize=(10, 6))
plt.plot(linex, liney, color='green', linewidth=2, label='True Function')
plt.scatter(x_train, y_train, alpha=0.7, label='Training Data')
plt.plot(xs, ys, 'r-', lw=2, label='Regularized Fit')

plt.title(f'N = {N}, M = {M}, ξ = {gzai:.3f}')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc='best', frameon=False)
plt.grid(True)
plt.show()

# 性能評価
ys_test = np.polyval(lss_c, x_test)

print(f'MSE (Training): {mean_squared_error(y_train, ys_train):.6f}')
print(f'MSE (Test): {mean_squared_error(y_test, ys_test):.6f}')

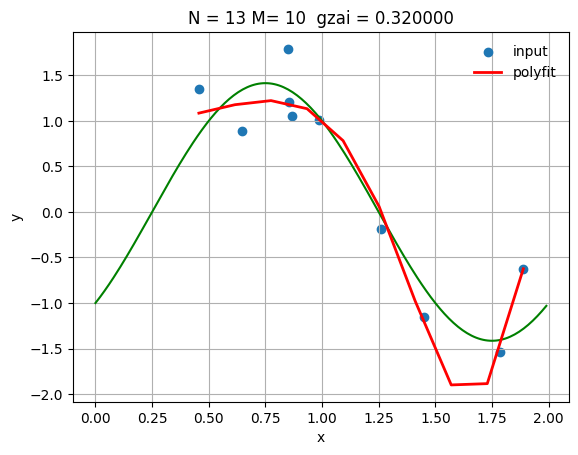
MSE (Training): 0.056731
MSE (Test): 0.268689

正則化の効果

適切な正則化パラメータを選択することで：

• 学習誤差とテスト誤差のバランスが取れる
• 過学習を防ぎ、汎化性能が向上する
• 数値的安定性が向上する

実験2：より複雑な関数近似

より大きなデータセットでの実験

設定：

• サンプル数：50（学習・テスト各25）
• 元の関数：$y = \sin(\pi x) - \cos(\pi x), \quad 0 < x < 5$
• ノイズ：平均0、標準偏差0.3の正規分布

sample = 50
sigma = 0.3

# ノイズ生成
e = np.random.normal(0, sigma, sample)

# より広い範囲での信号生成
x = np.random.uniform(0, 5, sample)
y = np.sin(np.pi*x) - np.cos(np.pi*x) + e

# データ分割
x_train, x_test, y_train, y_test = train_test_split(
    x, y, train_size=0.5, test_size=0.5, random_state=0
)

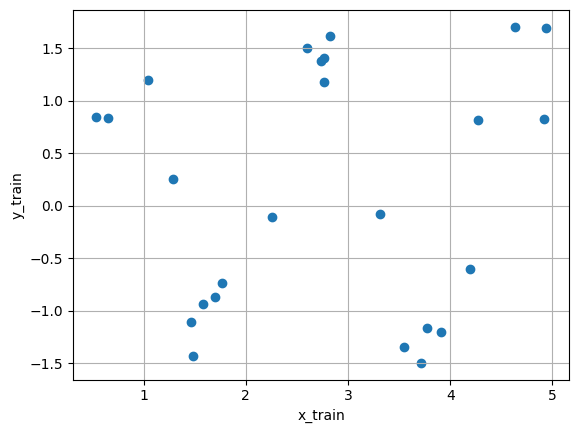
データの可視化

plt.figure(figsize=(12, 4))

plt.subplot(1, 2, 1)
plt.scatter(x_train, y_train, alpha=0.7)
plt.xlabel('x_train')
plt.ylabel('y_train')
plt.title('Training Data (Extended Range)')
plt.grid(True)

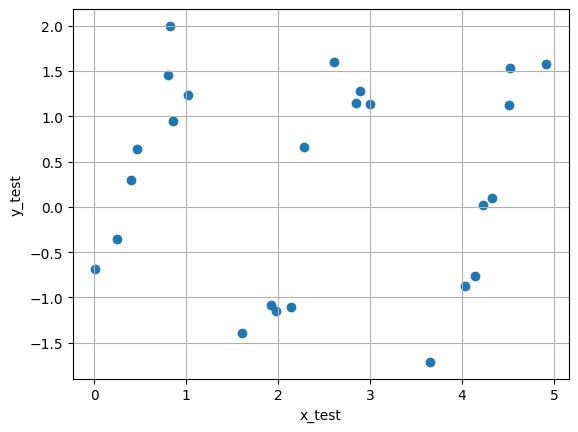
plt.subplot(1, 2, 2)
plt.scatter(x_test, y_test, alpha=0.7)
plt.xlabel('x_test')
plt.ylabel('y_test')
plt.title('Test Data (Extended Range)')
plt.grid(True)

plt.tight_layout()
plt.show()

解空間次元の影響（拡張版）

result = []

for N in range(2, 13):
    lss_c, M, Q = lms(x_train, y_train, N, 0.1)
    
    # 予測値計算
    ys_train = np.polyval(lss_c, x_train)
    ys_test = np.polyval(lss_c, x_test)
    
    # 誤差計算
    train_error = mean_squared_error(y_train, ys_train)
    test_error = mean_squared_error(y_test, ys_test)
    
    result.append([train_error, test_error])

# 結果可視化
diff = DataFrame(data=result, columns=['Training', 'Test'], 
                index=[n for n in range(2, 13)])

diff.plot(title=f'M = {M}, ξ = 0.1: Mean Squared Error')
plt.xlabel('N (Model Complexity)')
plt.ylabel('MSE')
plt.grid(True)
plt.show()

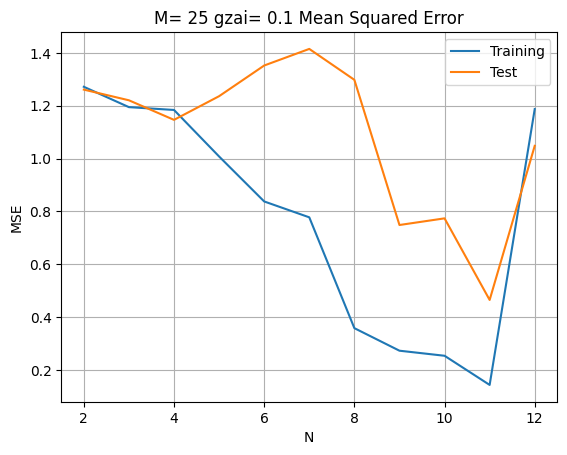
高次元での不安定性

$\xi = 0.1$ の場合、$N > 11$ で誤差が急激に増加します。これは基底関数 $\phi_k(x) = x^k$ が $x$ の範囲が大きいときに指数的に増加するためです。

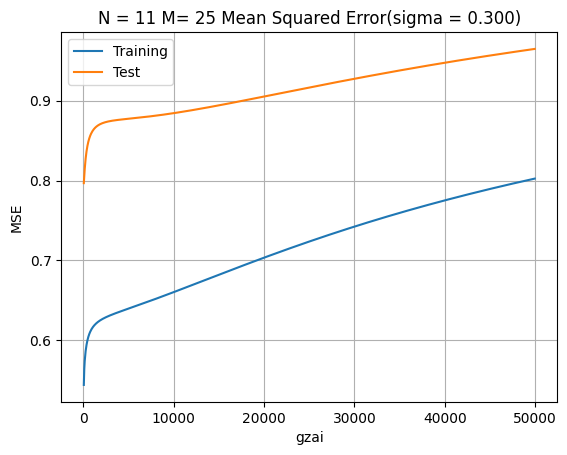
正則化パラメータの再調整

N = 11
result = []

# より大きな正則化パラメータの範囲を探索
for gzai_i in range(1, 1000):
    gzai = gzai_i * 50  # より大きな値を試行
    
    lss_c, M, Q = lms(x_train, y_train, N, gzai)
    
    # 予測と誤差計算
    ys_train = np.polyval(lss_c, x_train)
    ys_test = np.polyval(lss_c, x_test)
    
    train_error = mean_squared_error(y_train, ys_train)
    test_error = mean_squared_error(y_test, ys_test)
    
    result.append([gzai, train_error, test_error])

# 結果可視化
diff = DataFrame(data=result, columns=['gzai', 'Training', 'Test'])

diff.plot(x='gzai', y=['Training', 'Test'])
plt.title(f'N = {N}, M = {M}: Mean Squared Error (σ = {sigma:.3f})')
plt.xlabel('ξ (Regularization Parameter)')
plt.ylabel('MSE')
plt.grid(True)
plt.show()

小さな正則化パラメータでの結果

N = 11
gzai = 0.02

lss_c, M, Q = lms(x_train, y_train, N, gzai)

# 予測曲線生成
xs = np.linspace(np.min(x_train), np.max(x_train), M)
ys = np.polyval(lss_c, xs)

# 学習データ予測
ys_train = np.polyval(lss_c, x_train)

# 真の曲線
linex = np.arange(0, 5.0, 0.01)
liney = np.sin(np.pi*linex) - np.cos(np.pi*linex)

# 可視化
plt.figure(figsize=(12, 6))
plt.plot(linex, liney, color='green', linewidth=2, label='True Function')
plt.scatter(x_train, y_train, alpha=0.7, label='Training Data')
plt.plot(xs, ys, 'r-', lw=2, label='Regularized Fit')

plt.title(f'N = {N}, M = {M}, ξ = {gzai:.3f}')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc='best', frameon=False)
plt.grid(True)
plt.show()

# 性能評価
ys_test = np.polyval(lss_c, x_test)

print(f'MSE (Training): {mean_squared_error(y_train, ys_train):.6f}')
print(f'MSE (Test): {mean_squared_error(y_test, ys_test):.6f}')

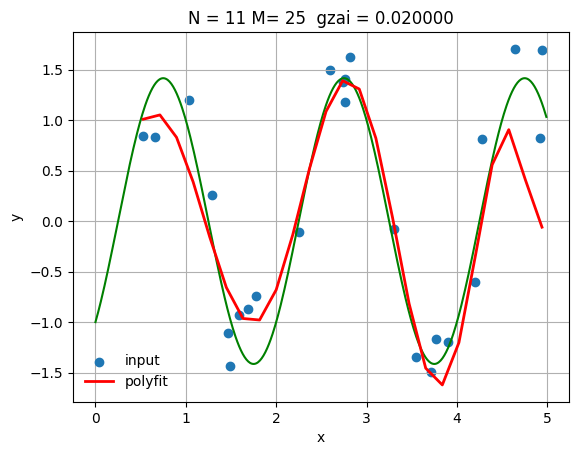
MSE (Training): 0.301408
MSE (Test): 0.335157

大きな正則化パラメータでの結果

N = 11
gzai = 10000

lss_c, M, Q = lms(x_train, y_train, N, gzai)

# 同様の可視化と評価
xs = np.linspace(np.min(x_train), np.max(x_train), M)
ys = np.polyval(lss_c, xs)
ys_train = np.polyval(lss_c, x_train)

linex = np.arange(0, 5.0, 0.01)
liney = np.sin(np.pi*linex) - np.cos(np.pi*linex)

plt.figure(figsize=(12, 6))
plt.plot(linex, liney, color='green', linewidth=2, label='True Function')
plt.scatter(x_train, y_train, alpha=0.7, label='Training Data')
plt.plot(xs, ys, 'r-', lw=2, label='Regularized Fit')

plt.title(f'N = {N}, M = {M}, ξ = {gzai:.0f}')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc='best', frameon=False)
plt.grid(True)
plt.show()

ys_test = np.polyval(lss_c, x_test)

print(f'MSE (Training): {mean_squared_error(y_train, ys_train):.6f}')
print(f'MSE (Test): {mean_squared_error(y_test, ys_test):.6f}')

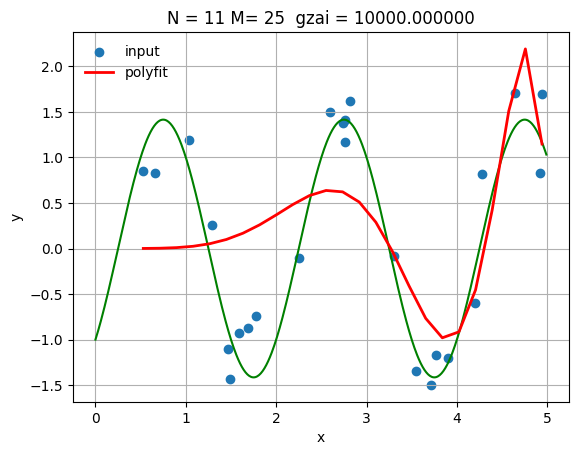
MSE (Training): 0.660348
MSE (Test): 0.884474

高次元での正則化効果

# 高次元モデルでの正則化効果を確認
result = []

for N in range(10, 17):
    lss_c, M, Q = lms(x_train, y_train, N, 10000)
    
    ys_train = np.polyval(lss_c, x_train)
    ys_test = np.polyval(lss_c, x_test)
    
    train_error = mean_squared_error(y_train, ys_train)
    test_error = mean_squared_error(y_test, ys_test)
    
    result.append([train_error, test_error])

diff = DataFrame(data=result, columns=['Training', 'Test'], 
                index=[n for n in range(10, 17)])

diff.plot(title=f'M = {M}, ξ = 10000: Mean Squared Error')
plt.xlabel('N (Model Complexity)')
plt.ylabel('MSE')
plt.grid(True)
plt.show()

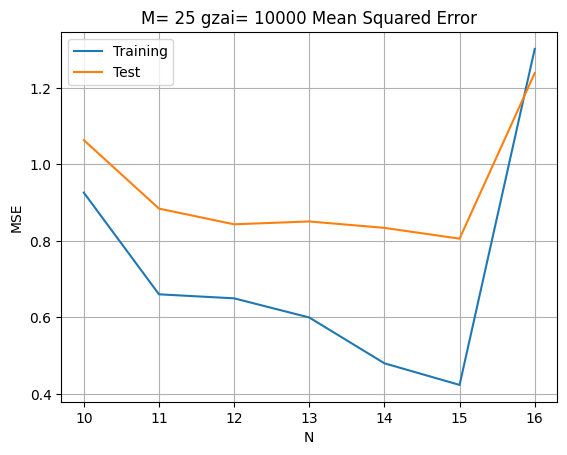
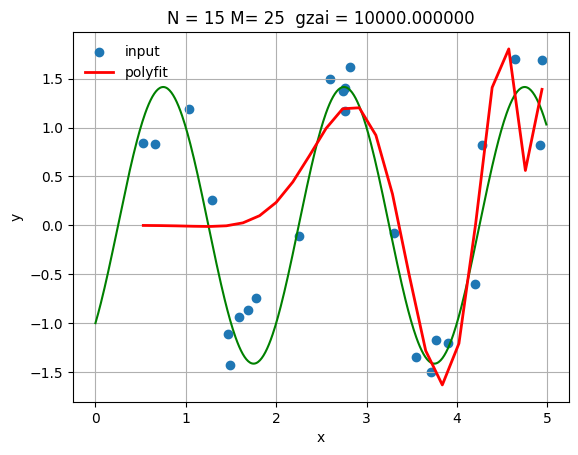
より高次元での最適化例

N = 15
gzai = 10000

lss_c, M, Q = lms(x_train, y_train, N, gzai)

xs = np.linspace(np.min(x_train), np.max(x_train), M)
ys = np.polyval(lss_c, xs)
ys_train = np.polyval(lss_c, x_train)

# 真の曲線
linex = np.arange(0, 5.0, 0.01)
liney = np.sin(np.pi*linex) - np.cos(np.pi*linex)

plt.figure(figsize=(12, 6))
plt.plot(linex, liney, color='green', linewidth=2, label='True Function')
plt.scatter(x_train, y_train, alpha=0.7, label='Training Data')
plt.plot(xs, ys, 'r-', lw=2, label='Regularized Fit')

plt.title(f'N = {N}, M = {M}, ξ = {gzai:.0f}')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc='best', frameon=False)
plt.grid(True)
plt.show()

ys_test = np.polyval(lss_c, x_test)

print(f'MSE (Training): {mean_squared_error(y_train, ys_train):.6f}')
print(f'MSE (Test): {mean_squared_error(y_test, ys_test):.6f}')

MSE (Training): 0.423424
MSE (Test): 0.805849

総合的な考察

1. モデル複雑さと正則化の関係

実験結果から、以下の重要な知見が得られました：

解空間次元 $N$ の効果：

• $N$ が大きいほど、モデルの表現能力が向上
• しかし、適切な正則化なしでは過学習のリスクが増大
• 基底関数 $\phi_k(x) = x^k$ の特性により、$x$ の範囲が大きい場合は特に注意が必要

正則化パラメータ $\xi$ の効果：

• 小さい値：学習誤差は小さいが、テスト誤差が大きい（過学習）
• 大きい値：安定した予測だが、アンダーフィッティングのリスク
• 最適値：バイアス-分散トレードオフの最適化

2. 実用的な指針

モデル選択戦略：

1. クロスバリデーション：正則化パラメータの選択
2. 情報量規準：AICやBICによるモデル比較
3. 早期停止：反復的手法での過学習防止

基底関数の設計：

• 入力データの範囲に適した基底関数の選択
• 直交基底（チェビシェフ多項式など）の使用を検討
• スプライン基底や動径基底関数の活用

3. 数値的安定性

計算上の注意点：

• 条件数の監視：$\text{cond}(H^T H + \xi I)$
• SVD分解の活用：数値的により安定な実装
• 適応的正則化：データに応じた動的調整

実用的な拡張

• リッジ回帰（L2正則化）：本手法の標準的な名称
• ラッソ回帰（L1正則化）：スパース解を得る手法
• エラスティックネット：L1とL2の組み合わせ
• ベイズ的解釈：正則化項を事前分布として解釈

まとめ

正則化ミニマムノルム解は、線形回帰における重要な手法であり、以下の特徴を持ちます：

1. 過学習の防止：正則化項により汎化性能を向上
2. 数値的安定性：特異値問題の回避
3. 柔軟なモデル選択：パラメータ調整による複雑さ制御

適切な正則化パラメータとモデル複雑さの選択により、実用的で堅牢な予測モデルを構築できます。現代の機械学習において、正則化は必須の技術となっており、深層学習を含む様々な手法の基礎となっています。

次のステップ

• カーネル法：非線形関数近似への拡張
• ガウス過程回帰：不確実性の定量化
• ベイズ線形回帰：確率的な解釈
• スパース回帰：特徴選択を含む手法