メインコンテンツまでスキップ

カルマンフィルタ (Kalman Filter)

カルマンフィルタは、ノイズを含む観測データから真の状態を推定する最適な線形推定手法です。本章では、スカラー変数のカルマンフィルタについて、観測雑音とシステム雑音の分散が状態推定値の精度およびカルマンゲインとの関係について、シミュレーション例を通して詳しく考察します。

概要​

カルマンフィルタは、予測と更新の2つのステップを繰り返すことで、時々刻々と変化するシステムの状態を最適に推定します。この手法は、航空宇宙、ロボティクス、金融工学など、幅広い分野で応用されている重要な技術です。

主な特徴​

  1. 最適性：平均二乗誤差を最小化する線形推定器
  2. 再帰性：過去のデータを保存せずに逐次更新が可能
  3. リアルタイム性：オンライン処理に適している
  4. 理論的保証：ガウシアンノイズ下での最適性が数学的に証明済み

問題設定​

基本問題​

スカラー変数のカルマンフィルタについて、観測雑音とシステム雑音の分散を変化させ、これらと状態推定値の精度およびカルマンゲインとの関係について、シミュレーション例を通して考察します。

設定パラメータ：

  • システム雑音の分散：σw2\sigma_w^2
  • 観測雑音の分散：σ2\sigma^2
  • 係数：F=1,H=1F = 1, H = 1

初期値：

  • 状態推定値の初期値：xˉ0=0\bar{x}_0 = 0
  • 推定誤差分散の初期値：v0=σ2v_0 = \sigma^2

理論的背景​

2.1 システムモデル​

カルマンフィルタは以下の2つのモデルに基づいています：

状態遷移モデル（システムモデル）： xk=Fxk−1+wkx_k = Fx_{k-1} + w_k

ここで：

  • xkx_k：時刻 tkt_k におけるシステム状態
  • FF：状態遷移行列
  • wk∼N(0,σw2)w_k \sim \mathcal{N}(0, \sigma_w^2)：システム雑音（プロセスノイズ）

観測モデル（測定モデル）： yk=Hxk+εky_k = Hx_k + \varepsilon_k

ここで：

  • yky_k：時刻 tkt_k における観測値
  • HH：観測行列
  • εk∼N(0,σ2)\varepsilon_k \sim \mathcal{N}(0, \sigma^2)：観測雑音（測定ノイズ）

2.2 カルマンフィルタの更新式​

カルマンフィルタは以下の手順で状態を推定します：

予測ステップ（時間更新）：

x^k∣k−1=Fx^k−1∣k−1Pk∣k−1=FPk−1∣k−1FT+Q\begin{aligned} \hat{x}_{k|k-1} &= F\hat{x}_{k-1|k-1} \\ P_{k|k-1} &= FP_{k-1|k-1}F^T + Q \end{aligned}

更新ステップ（観測更新）：

Kk=Pk∣k−1HTHPk∣k−1HT+Rx^k∣k=x^k∣k−1+Kk(yk−Hx^k∣k−1)Pk∣k=(I−KkH)Pk∣k−1\begin{aligned} K_k &= \frac{P_{k|k-1}H^T}{HP_{k|k-1}H^T + R} \\ \hat{x}_{k|k} &= \hat{x}_{k|k-1} + K_k(y_k - H\hat{x}_{k|k-1}) \\ P_{k|k} &= (I - K_kH)P_{k|k-1} \end{aligned}

スカラーケースでの簡略化： F=H=1F = H = 1 の場合：

pk−1=vk−1+σw2κ=pk−1σ2+pk−1vk=(1−κ)pk−1x^k=x^k−1+κ(yk−x^k−1)\begin{aligned} p_{k-1} &= v_{k-1} + \sigma_w^2 \\ \kappa &= \frac{p_{k-1}}{\sigma^2 + p_{k-1}} \\ v_k &= (1 - \kappa)p_{k-1} \\ \hat{x}_k &= \hat{x}_{k-1} + \kappa(y_k - \hat{x}_{k-1}) \end{aligned}
カルマンゲインの意味

カルマンゲイン κ\kappa は、予測値と観測値の重み付けを決定する重要なパラメータです：

  • κ→1\kappa \rightarrow 1：観測値を重視（観測ノイズが小さい）
  • κ→0\kappa \rightarrow 0：予測値を重視（システムノイズが小さい）

実装とシミュレーション​

3.1 必要なライブラリのインポート​

# 基本ライブラリ
import numpy as np
import scipy as sp
import pandas as pd
from pandas import Series, DataFrame

# 可視化ライブラリ
import matplotlib.pyplot as plt
import matplotlib as mpl

# 設定
np.set_printoptions(precision=3)
plt.style.use('seaborn-v0_8')

def kf_scalar(F, H, Q, R, y, xhat, V):
    """
    スカラーカルマンフィルタの更新関数
    
    Parameters:
    -----------
    F : float
        状態遷移係数
    H : float
        観測係数  
    Q : float
        システム雑音の分散 (σ_w^2)
    R : float
        観測雑音の分散 (σ^2)
    y : float
        現在の観測値
    xhat : float
        前時刻の状態推定値
    V : float
        前時刻の推定誤差分散
        
    Returns:
    --------
    xhat : float
        更新された状態推定値
    V : float
        更新された推定誤差分散
    G : float
        カルマンゲイン
    """
    # ①誤差分散p(k-1) - 予測ステップ
    P = F * F * V + Q
    
    # ②カルマンゲインκ
    G = P * H / (H * H * P + R)
    
    # ③事後分布の分散行列v(k) - 更新ステップ
    V = (1 - G * H) * P
    
    # ④推定値x(k) - 更新ステップ
    xhat = F * xhat + G * (y - H * F * xhat)
    
    return (xhat, V, G)

3.2 基本シミュレーション​

パラメータ設定：

# システムパラメータ
F = 1  # 状態遷移係数
H = 1  # 観測係数

# ノイズパラメータ
sigma_w = 2.0  # システム雑音の標準偏差
sigma = 2.0    # 観測雑音の標準偏差

Q = sigma_w**2  # システム雑音の分散
R = sigma**2    # 観測雑音の分散
K = 300         # データ数

# 初期値設定
x = 0.0      # 状態量の初期値
xhat = 0.0   # 状態推定値の初期値
V = 0        # 事後分布の分散の初期値

# 再現性のためのランダムシード固定
np.random.seed(0)

print(f"シミュレーション設定:")
print(f"システム雑音標準偏差: σ_w = {sigma_w}")
print(f"観測雑音標準偏差: σ = {sigma}")
print(f"データ数: K = {K}")

メインシミュレーション：

result = []

for k in range(K):
    # 雑音信号の生成
    w = np.random.normal(0, sigma_w)  # システム雑音
    v = np.random.normal(0, sigma)    # 観測雑音
    
    # 真の状態値の計算（システムモデル）
    x = F * x + w
    
    # 観測値の計算（観測モデル）
    y = H * x + v
    
    # カルマンフィルタによる状態推定
    xhat, V, G = kf_scalar(F, H, Q, R, y, xhat, V)
    
    # 結果の記録
    result.append([k, x, y, xhat, V, G])

# データフレームとして整理
df = DataFrame(data=result, columns=['k', 'x', 'y', 'xhat', 'V', 'G'])

# 結果の表示（最初の10行と最後の5行）
print("=== シミュレーション結果（抜粋） ===")
print(df.head(10))
print("...")
print(df.tail(5))

# 統計的性能の評価
mse = np.mean((df['x'] - df['xhat'])**2)
print(f"\n=== 性能評価 ===")
print(f"平均二乗誤差 (MSE): {mse:.6f}")
print(f"最終カルマンゲイン: {df['G'].iloc[-1]:.6f}")
print(f"最終推定誤差分散: {df['V'].iloc[-1]:.6f}")

3.3 結果の可視化​

# 推定結果の描画
fig, axes = plt.subplots(nrows=4, ncols=1, figsize=(12, 16))

# 1. 全体の軌跡比較
df.plot(ax=axes[0], x='k', y=['x', 'xhat', 'y'], 
        color=["black", "red", "green"], linewidth=2)
axes[0].set_xlabel("時刻 k")
axes[0].set_ylabel("値")
axes[0].set_title("状態推定結果（全体比較）")
axes[0].set_xlim(0, K)
axes[0].legend(['真値 x', '推定値 x̂', '観測値 y'])
axes[0].grid(True, alpha=0.3)

# 2. 真値と推定値の比較
df.plot(ax=axes[1], x='k', y=['x', 'xhat'], 
        color=["black", "red"], linewidth=2)
axes[1].set_xlabel("時刻 k")
axes[1].set_ylabel("状態値")
axes[1].set_title("真値と推定値の比較")
axes[1].set_xlim(0, K)
axes[1].legend(['真値 x', '推定値 x̂'])
axes[1].grid(True, alpha=0.3)

# 3. カルマンゲインの時間変化
df.plot(ax=axes[2], x='k', y='G', color="red", linewidth=2)
axes[2].set_xlabel("時刻 k")
axes[2].set_ylabel("カルマンゲイン κ")
axes[2].set_title("カルマンゲインの収束過程")
axes[2].set_xlim(0, K)
axes[2].set_ylim(0, 1)
axes[2].grid(True, alpha=0.3)

# 4. 推定誤差分散の時間変化
df.plot(ax=axes[3], x='k', y='V', color="blue", linewidth=2)
axes[3].set_xlabel("時刻 k")
axes[3].set_ylabel("推定誤差分散 v")
axes[3].set_title("推定誤差分散の収束過程")
axes[3].set_xlim(0, K)
axes[3].grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

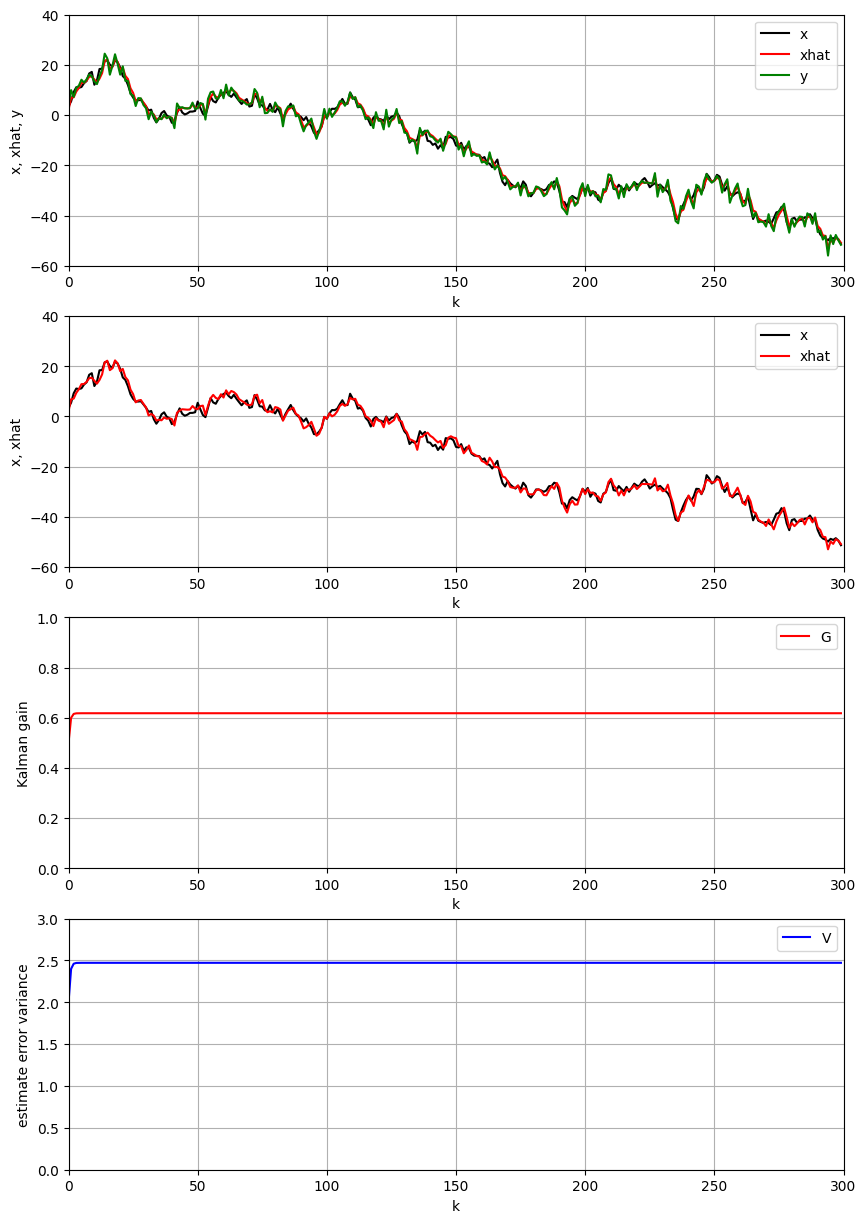
Basic Kalman Filter Results

基本結果の解釈
  • 推定値（赤線）：真値（黒線）をよく追従している
  • カルマンゲイン：初期値から定常値に収束
  • 推定誤差分散：時間とともに減少し、定常値に収束
  • システム雑音と観測雑音が同程度の場合、バランスの取れた推定が実現

パラメータ感度分析​

4.1 システム雑音の影響（σ_w の増加）​

システム雑音の標準偏差を σw=15\sigma_w = 15、観測雑音の標準偏差を σ=2\sigma = 2 に設定して影響を調べます。

# パラメータ設定（システム雑音大）
F = 1; H = 1
sigma_w = 15.0  # システム雑音標準偏差（大）
sigma = 2.0     # 観測雑音標準偏差（小）

Q = sigma_w**2
R = sigma**2
K = 300

# 初期値設定
x = 0.0; xhat = 0.0; V = 0

# ランダムシード固定（比較のため）
np.random.seed(0)

result_high_system_noise = []

for k in range(K):
    # 雑音信号の生成
    w = np.random.normal(0, sigma_w)
    v = np.random.normal(0, sigma)
    
    # 状態と観測の更新
    x = F * x + w
    y = H * x + v
    
    # カルマンフィルタ更新
    xhat, V, G = kf_scalar(F, H, Q, R, y, xhat, V)
    result_high_system_noise.append([k, x, y, xhat, V, G])

df_high_sys = DataFrame(data=result_high_system_noise, 
                       columns=['k', 'x', 'y', 'xhat', 'V', 'G'])

# 結果の可視化
fig, axes = plt.subplots(nrows=4, ncols=1, figsize=(12, 16))

# データの範囲を調整して可視化
y_range = [-100, 150]

df_high_sys.plot(ax=axes[0], x='k', y=['x', 'xhat', 'y'], 
                color=["black", "red", "green"], linewidth=2)
axes[0].set_xlabel("時刻 k")
axes[0].set_ylabel("値")
axes[0].set_title(f"高システム雑音環境 (σ_w = {sigma_w}, σ = {sigma})")
axes[0].set_xlim(0, K)
axes[0].set_ylim(y_range)
axes[0].legend(['真値 x', '推定値 x̂', '観測値 y'])
axes[0].grid(True, alpha=0.3)

df_high_sys.plot(ax=axes[1], x='k', y=['x', 'xhat'], 
                color=["black", "red"], linewidth=2)
axes[1].set_xlabel("時刻 k")
axes[1].set_ylabel("状態値")
axes[1].set_title("真値と推定値の比較（高システム雑音）")
axes[1].set_xlim(0, K)
axes[1].set_ylim(y_range)
axes[1].legend(['真値 x', '推定値 x̂'])
axes[1].grid(True, alpha=0.3)

df_high_sys.plot(ax=axes[2], x='k', y='G', color="red", linewidth=2)
axes[2].set_xlabel("時刻 k")
axes[2].set_ylabel("カルマンゲイン κ")
axes[2].set_title("カルマンゲイン（高システム雑音）")
axes[2].set_xlim(0, K)
axes[2].set_ylim(0, 1.0)
axes[2].grid(True, alpha=0.3)

df_high_sys.plot(ax=axes[3], x='k', y='V', color="blue", linewidth=2)
axes[3].set_xlabel("時刻 k")
axes[3].set_ylabel("推定誤差分散 v")
axes[3].set_title("推定誤差分散（高システム雑音）")
axes[3].set_xlim(0, K)
axes[3].grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

# 性能評価
print(f"=== 高システム雑音環境の結果 ===")
print(f"システム雑音標準偏差: σ_w = {sigma_w}")
print(f"観測雑音標準偏差: σ = {sigma}")
print(f"最終カルマンゲイン: {df_high_sys['G'].iloc[-1]:.6f}")
print(f"最終推定誤差分散: {df_high_sys['V'].iloc[-1]:.6f}")
print(f"平均二乗誤差: {np.mean((df_high_sys['x'] - df_high_sys['xhat'])**2):.6f}")

High System Noise Results

4.2 観測雑音の影響（σ の増加）​

観測雑音の標準偏差を σ=15\sigma = 15、システム雑音の標準偏差を σw=2\sigma_w = 2 に設定して影響を調べます。

# パラメータ設定（観測雑音大）
F = 1; H = 1
sigma_w = 2.0   # システム雑音標準偏差（小）
sigma = 15.0    # 観測雑音標準偏差（大）

Q = sigma_w**2
R = sigma**2
K = 300

# 初期値設定
x = 0.0; xhat = 0.0; V = 0

# ランダムシード固定（比較のため）
np.random.seed(0)

result_high_obs_noise = []

for k in range(K):
    # 雑音信号の生成
    w = np.random.normal(0, sigma_w)
    v = np.random.normal(0, sigma)
    
    # 状態と観測の更新
    x = F * x + w
    y = H * x + v
    
    # カルマンフィルタ更新
    xhat, V, G = kf_scalar(F, H, Q, R, y, xhat, V)
    result_high_obs_noise.append([k, x, y, xhat, V, G])

df_high_obs = DataFrame(data=result_high_obs_noise, 
                       columns=['k', 'x', 'y', 'xhat', 'V', 'G'])

# 結果の可視化
fig, axes = plt.subplots(nrows=4, ncols=1, figsize=(12, 16))

# データの範囲を調整
y_range = [-85, 40]

df_high_obs.plot(ax=axes[0], x='k', y=['x', 'xhat', 'y'], 
                color=["black", "red", "green"], linewidth=2)
axes[0].set_xlabel("時刻 k")
axes[0].set_ylabel("値")
axes[0].set_title(f"高観測雑音環境 (σ_w = {sigma_w}, σ = {sigma})")
axes[0].set_xlim(0, K)
axes[0].set_ylim(y_range)
axes[0].legend(['真値 x', '推定値 x̂', '観測値 y'])
axes[0].grid(True, alpha=0.3)

df_high_obs.plot(ax=axes[1], x='k', y=['x', 'xhat'], 
                color=["black", "red"], linewidth=2)
axes[1].set_xlabel("時刻 k")
axes[1].set_ylabel("状態値")
axes[1].set_title("真値と推定値の比較（高観測雑音）")
axes[1].set_xlim(0, K)
axes[1].set_ylim(y_range)
axes[1].legend(['真値 x', '推定値 x̂'])
axes[1].grid(True, alpha=0.3)

df_high_obs.plot(ax=axes[2], x='k', y='G', color="red", linewidth=2)
axes[2].set_xlabel("時刻 k")
axes[2].set_ylabel("カルマンゲイン κ")
axes[2].set_title("カルマンゲイン（高観測雑音）")
axes[2].set_xlim(0, K)
axes[2].set_ylim(0, 0.15)
axes[2].grid(True, alpha=0.3)

df_high_obs.plot(ax=axes[3], x='k', y='V', color="blue", linewidth=2)
axes[3].set_xlabel("時刻 k")
axes[3].set_ylabel("推定誤差分散 v")
axes[3].set_title("推定誤差分散（高観測雑音）")
axes[3].set_xlim(0, K)
axes[3].set_ylim(0, 30)
axes[3].grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

# 性能評価
print(f"=== 高観測雑音環境の結果 ===")
print(f"システム雑音標準偏差: σ_w = {sigma_w}")
print(f"観測雑音標準偏差: σ = {sigma}")
print(f"最終カルマンゲイン: {df_high_obs['G'].iloc[-1]:.6f}")
print(f"最終推定誤差分散: {df_high_obs['V'].iloc[-1]:.6f}")
print(f"平均二乗誤差: {np.mean((df_high_obs['x'] - df_high_obs['xhat'])**2):.6f}")

High Observation Noise Results

詳細な考察と理論的解析​

4.1 システム雑音の影響（σ_w の増加）​

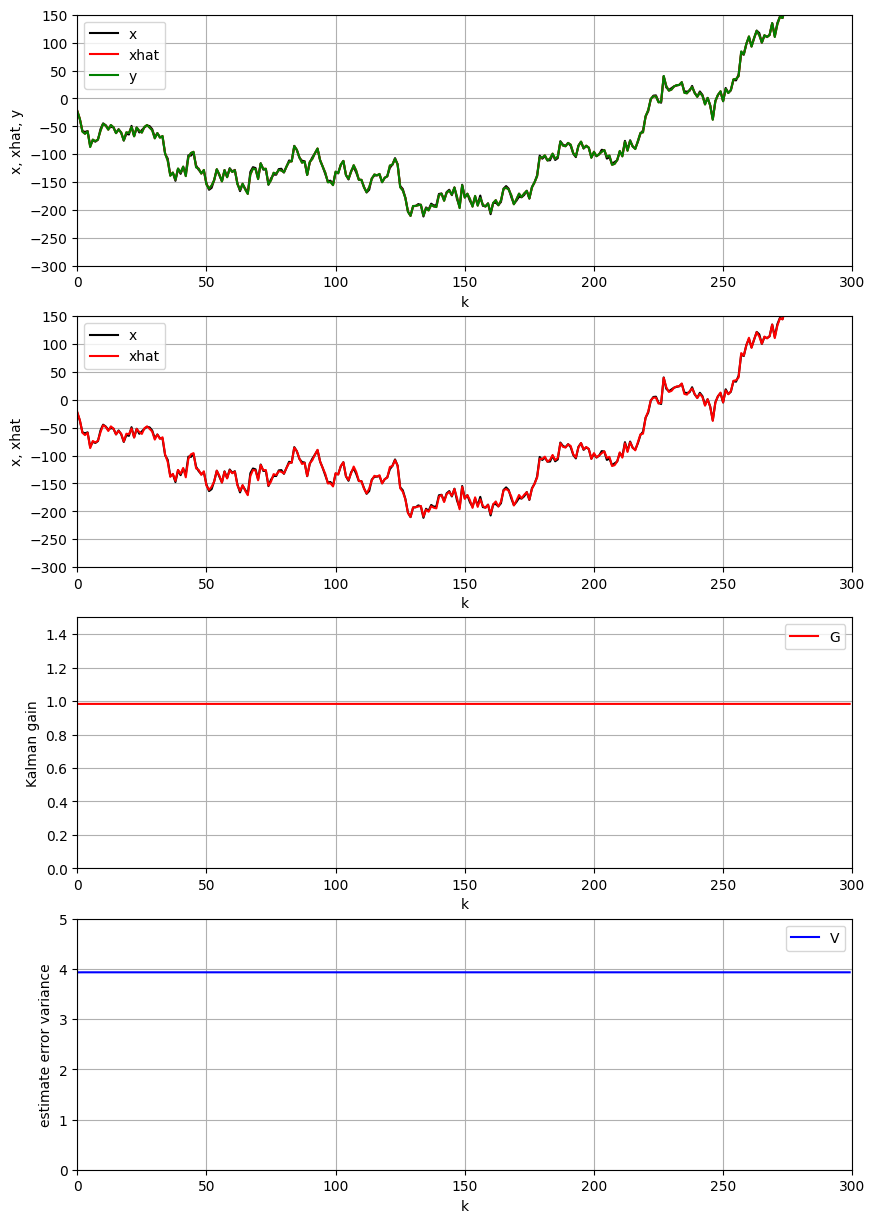
観察された現象：

  • カルマンゲインが大きくなる（約0.98）
  • 推定値が観測値により強く依存する
  • 真値の急激な変化によく追従する

理論的解析：

カルマンゲインの式から： κ=pk−1Hσ2+H2pk−1=Hσ2pk−1+H2\kappa = \frac{p_{k-1}H}{\sigma^2 + H^2p_{k-1}} = \frac{H}{\frac{\sigma^2}{p_{k-1}} + H^2}

ここで、pk−1=F2vk−1+σw2p_{k-1} = F^2v_{k-1} + \sigma_w^2 であり、σw\sigma_w が大きいほど pk−1p_{k-1} が大きくなるため、κ\kappa も大きくなります。

物理的解釈：

  1. 高システム雑音：システムモデルによる予測の不確実性が大きい
  2. 観測重視：不確実な予測よりも、実際の観測値を重視する戦略が最適
  3. 追従性向上：急激な状態変化に対する追従性が向上
  4. トレードオフ：追従性は向上するが、ノイズの影響も受けやすくなる
システム雑音増加の効果

利点：

  • 急激な状態変化への追従性向上
  • モデル不確実性への適応

欠点：

  • ノイズの影響を受けやすい
  • 推定値の変動が大きくなる

4.2 観測雑音の影響（σ の増加）​

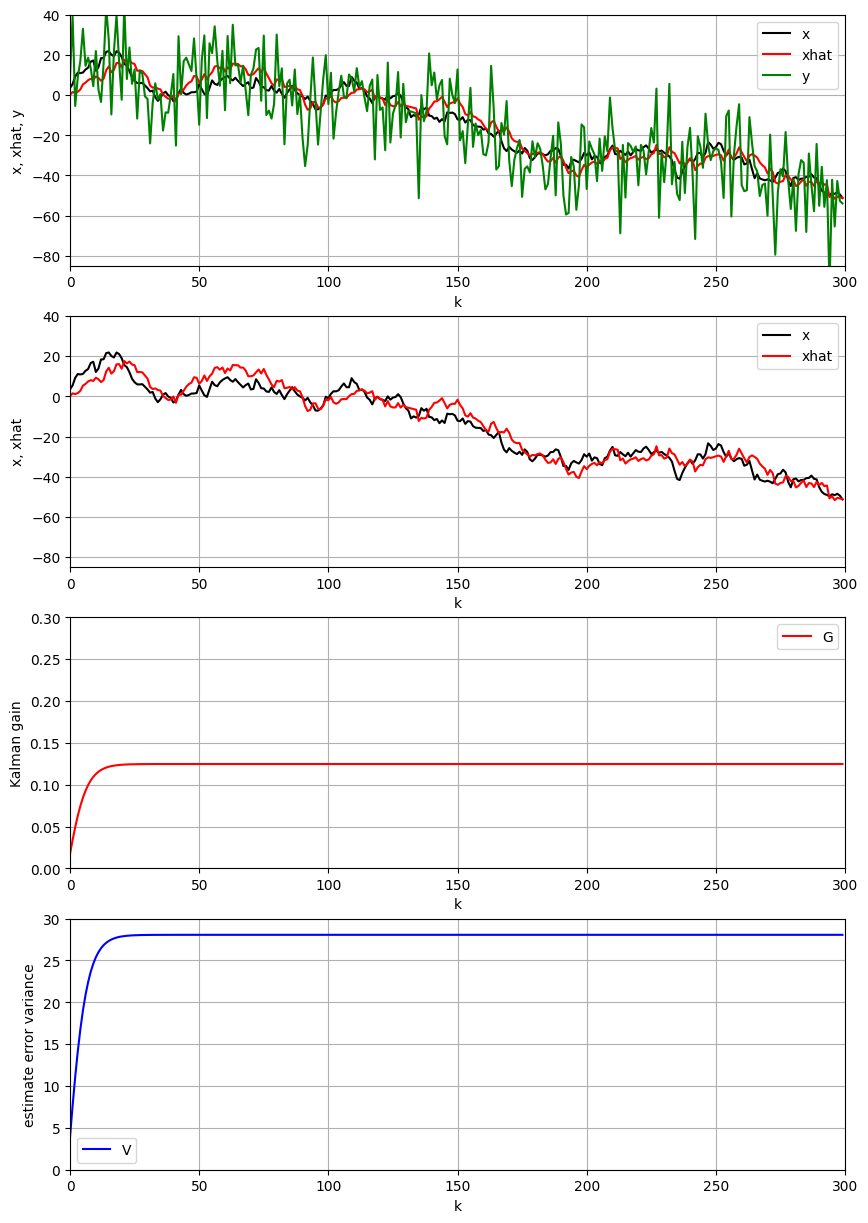
観察された現象：

  • カルマンゲインが小さくなる（約0.12）
  • 推定値がシステムモデルの予測により強く依存する
  • 観測値の急激な変化に追従しにくい

理論的解析：

カルマンゲインの式から： κ=pk−1Hσ2+H2pk−1\kappa = \frac{p_{k-1}H}{\sigma^2 + H^2p_{k-1}}

σ2\sigma^2 が大きくなると、分母が大きくなるため κ\kappa は小さくなります。

物理的解釈：

  1. 高観測雑音：観測値の信頼性が低い
  2. 予測重視：ノイズの多い観測よりも、システムモデルによる予測を重視
  3. 平滑化効果：推定値が急激に変化しにくく、平滑化される
  4. 遅延の発生：真の状態変化に対する応答が遅れる
観測雑音増加の注意点

利点：

  • ノイズの多い観測に対する頑健性
  • 推定値の安定性向上

欠点：

  • 真の状態変化への応答遅延
  • 過度の平滑化による情報損失

4.3 カルマンゲインの定常値解析​

カルマンゲインは時間とともに定常値に収束します。この定常値は以下の方程式を解くことで求められます：

κ∞=p∞HR+H2p∞\kappa_{\infty} = \frac{p_{\infty}H}{R + H^2p_{\infty}}

ここで、p∞p_{\infty} は定常状態での予測誤差分散であり、以下のリカッチ方程式の解です：

p∞=F2v∞+Qp_{\infty} = F^2v_{\infty} + Q v∞=(1−κ∞H)p∞v_{\infty} = (1 - \kappa_{\infty}H)p_{\infty}

これらから： p∞=Q+Q2+4QR2p_{\infty} = \frac{Q + \sqrt{Q^2 + 4QR}}{2}

数値例での検証：

  1. 基本ケース (σw=σ=2\sigma_w = \sigma = 2)：

    • Q=R=4Q = R = 4
    • p∞=4.472p_{\infty} = 4.472
    • κ∞=0.618\kappa_{\infty} = 0.618

  2. 高システム雑音 (σw=15,σ=2\sigma_w = 15, \sigma = 2)：

    • Q=225,R=4Q = 225, R = 4
    • p∞=115.97p_{\infty} = 115.97
    • κ∞=0.983\kappa_{\infty} = 0.983

  3. 高観測雑音 (σw=2,σ=15\sigma_w = 2, \sigma = 15)：

    • Q=4,R=225Q = 4, R = 225
    • p∞=18.97p_{\infty} = 18.97
    • κ∞=0.078\kappa_{\infty} = 0.078

実用的な応用と設計指針​

応用分野​

  1. 航空宇宙工学

    • 航空機・宇宙船の姿勢推定
    • GPS/INS統合航法システム

  2. ロボティクス

    • 移動ロボットの位置推定
    • マニピュレータの状態推定

  3. 金融工学

    • 株価・為替レートの予測
    • ボラティリティの推定

  4. 信号処理

    • 音声・画像のノイズ除去
    • センサー信号の平滑化

設計指針​

1. ノイズパラメータの設定

  • システム雑音分散 QQ：システムモデルの不確実性を反映
  • 観測雑音分散 RR：センサーの測定精度を反映
  • 経験的手法：実データによるパラメータ同定

2. 初期値の設定

  • 初期状態推定値：可能な限り真値に近い値
  • 初期誤差分散：不確実性が大きい場合は大きな値

3. 数値的安定性

  • ヨーゼフ形式：数値誤差による非正定値性を回避
  • 平方根フィルタ：より安定な数値計算

4. 適応的手法

  • 革新系列の監視：フィルタ性能の診断
  • 適応カルマンフィルタ：未知パラメータの同時推定

拡張手法​

1. 拡張カルマンフィルタ (EKF)

  • 非線形システムへの適用
  • ヤコビアンによる線形化

2. アンセンテッドカルマンフィルタ (UKF)

  • シグマポイントによる非線形変換
  • 高次の統計的性質を保持

3. 粒子フィルタ

  • 非ガウシアンノイズへの対応
  • モンテカルロ手法による近似

まとめ​

カルマンフィルタは、ノイズを含む観測データから最適な状態推定を行う強力な手法です。本章で得られた主要な知見をまとめます：

主要な結論​

  1. システム雑音の増加

    • カルマンゲインが大きくなり、観測重視の推定
    • 急激な状態変化への追従性が向上
    • ノイズの影響を受けやすくなる

  2. 観測雑音の増加

    • カルマンゲインが小さくなり、予測重視の推定
    • 推定値が平滑化され、ノイズに頑健
    • 真の状態変化への応答が遅れる

  3. 最適なバランス

    • システム雑音と観測雑音の比率が重要
    • 応用分野に応じた適切なパラメータ設定が必要

理論的意義​

カルマンフィルタは、ベイズ推定の枠組みにおける最適解として位置づけられます：

  • 事前情報：システムモデルによる予測
  • 観測情報：センサーによる測定値
  • 事後推定：両者を最適に結合した状態推定

実用的価値​

現代の制御・推定理論において、カルマンフィルタは基礎的かつ重要な技術です。GPS、自動運転、ドローン制御など、我々の身近な技術の多くにカルマンフィルタが応用されており、その理解は工学系学生にとって必須の知識となっています。

次のステップ
  • 多変数カルマンフィルタ：ベクトル・行列を用いた一般化
  • 非線形フィルタ：EKF、UKF、粒子フィルタ
  • 適応フィルタ：パラメータの同時推定
  • 平滑化手法：後方平滑化による精度向上