中心極限定理 (Central Limit Theorem)

Made by Youkoutaku

中心極限定理は統計学における最も重要な定理の一つです。この記事では、正規分布の再生性と中心極限定理について、Pythonを用いたシミュレーションで実践的に理解していきます。

ライブラリのインポート

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
%matplotlib inline
%precision 3

np.random.seed(0)

---

1. 正規分布の再生性 (Reproductive Property of Normal Distribution)

正規分布の重要な性質の一つである再生性について検証します。

理論的背景

$X_1, X_2$ がそれぞれ正規分布 $N(m_1,σ_1^2)$ と $N(m_2,σ_2^2)$ に従うとき、その和 $X_1 + X_2$ は正規分布 $N(m_1 + m_2, σ_1^2 + σ_2^2)$ に従います。

シミュレーション設定

以下のパラメータで検証を行います：

• $m_1 = 0, m_2 = 1$
• $σ_1 = 0.1, σ_2 = 1$
• $m = m_1 + m_2, σ^2 = σ_1^2 + σ_2^2$

$X_1 + X_2$ が $N(m, σ^2)$ に従うかどうかをシミュレーションで検証します。

# パラメータ設定
m1 = 0
m2 = 1
sigma1 = 0.1
sigma2 = 1

# X1の生成と可視化
x1 = stats.norm.rvs(loc=m1, scale=sigma1, size=10000, random_state=0)
plt.hist(x1, density=True, bins=100)
plt.grid(True)
plt.title('正規分布 X1 ~ N(0, 0.1²)')
plt.xlabel('値')
plt.ylabel('密度')
plt.show()

# X2の生成と可視化
x2 = stats.norm.rvs(loc=m2, scale=sigma2, size=10000, random_state=0)
plt.hist(x2, density=True, bins=100)
plt.grid(True)
plt.title('正規分布 X2 ~ N(1, 1²)')
plt.xlabel('値')
plt.ylabel('密度')
plt.show()

再生性の検証

# X1 + X2の分布
plt.hist(x1+x2, density=True, bins=100)
plt.grid(True)
plt.title('X1 + X2の分布')
plt.xlabel('値')
plt.ylabel('密度')
plt.show()

# 理論的な合成分布 N(m1+m2, σ1²+σ2²)
m = m1 + m2
sigma = np.sqrt(sigma1**2 + sigma2**2)  # 標準偏差は分散の平方根

x = stats.norm.rvs(loc=m, scale=sigma, size=10000, random_state=0)
plt.hist(x, density=True, bins=100)
plt.grid(True)
plt.title(f'理論的分布 N({m}, {sigma:.3f}²)')
plt.xlabel('値')
plt.ylabel('密度')
plt.show()

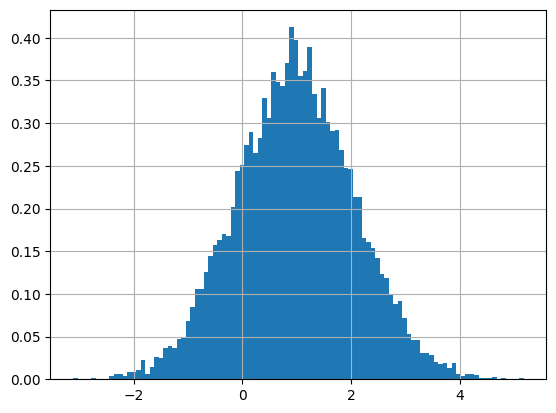
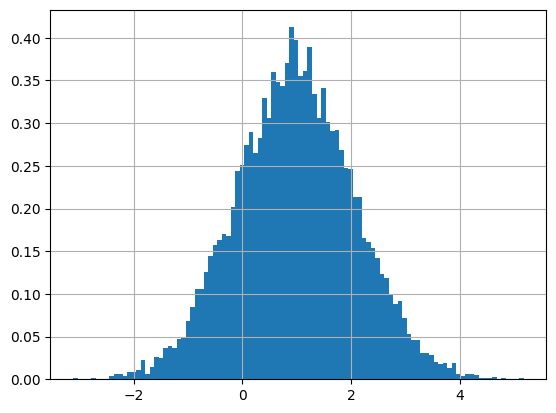
検証結果

$X_1 + X_2$ は $N(m, σ^2)$ に従うことが確認できました。これは正規分布の再生性を示しています。

---

2. 中心極限定理 (Central Limit Theorem)

中心極限定理は、任意の分布に従う独立同分布の確率変数の和は、試行回数が増加するにつれて正規分布に近づくという重要な定理です。

理論的背景

$X_1, X_2, ..., X_n$ を同一の分布（平均 $μ$、分散 $σ^2$）に従う独立な確率変数とするとき、標本平均 $\bar{X}_n = \frac{1}{n}(X_1 + X_2 + ... + X_n)$ は、$n$ が大きくなるにつれて正規分布 $N(μ, \frac{σ^2}{n})$ に近づきます。

指数分布による検証

指数分布は非対称な分布ですが、中心極限定理により、その和は正規分布に近づくはずです。

# 指数分布による中心極限定理の検証
def function_central_theory_expon(N):
    lambda_ = 1
    for i in range(N):
        new_data_expon = stats.expon.rvs(scale=1/lambda_, size=10000)
        if i == 0:
            data_expon = new_data_expon
        else:
            data_expon = data_expon + new_data_expon
    
    plt.hist(data_expon, density=True, bins=50, alpha=0.7)
    plt.title(f'指数分布の和 (N={N})')
    plt.xlabel('値')
    plt.ylabel('密度')
    plt.grid(True)
    plt.show()

# N=1, 10, 100での検証
function_central_theory_expon(1)
function_central_theory_expon(10)
function_central_theory_expon(100)

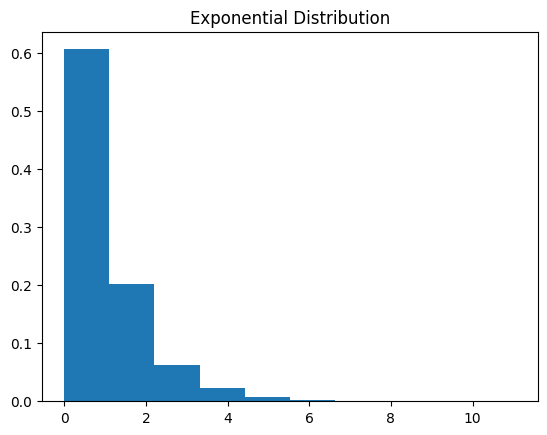
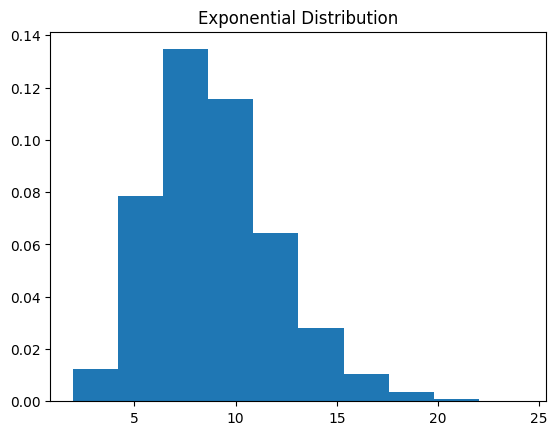
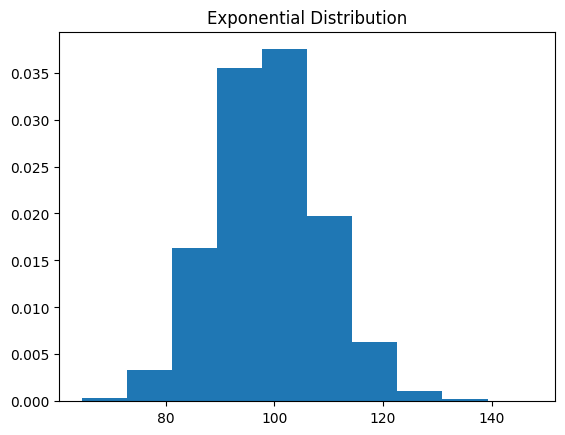
幾何分布による検証

離散分布である幾何分布についても同様に検証します。

# 幾何分布による中心極限定理の検証
def function_central_theory_geom(N):
    p = 0.5
    for i in range(N):
        rv_geom = stats.geom(p)
        new_data_geom = rv_geom.rvs(size=10000)
        if i == 0:
            data_geom = new_data_geom
        else:
            data_geom = data_geom + new_data_geom
    
    plt.hist(data_geom, density=True, bins=50, alpha=0.7)
    plt.title(f'幾何分布の和 (N={N})')
    plt.xlabel('値')
    plt.ylabel('密度')
    plt.grid(True)
    plt.show()

# N=1, 10, 100での検証
function_central_theory_geom(1)
function_central_theory_geom(10)
function_central_theory_geom(100)

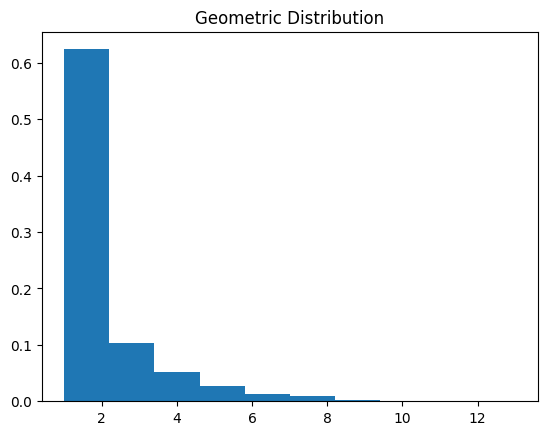
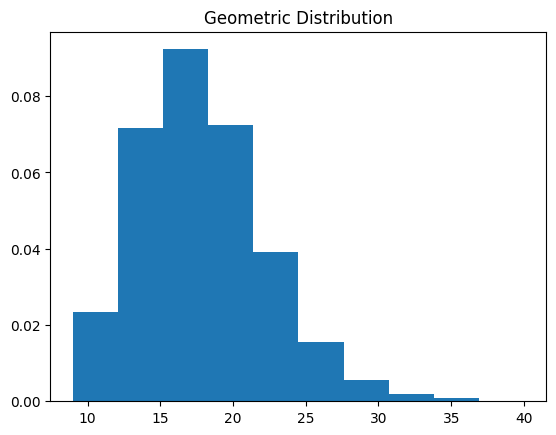
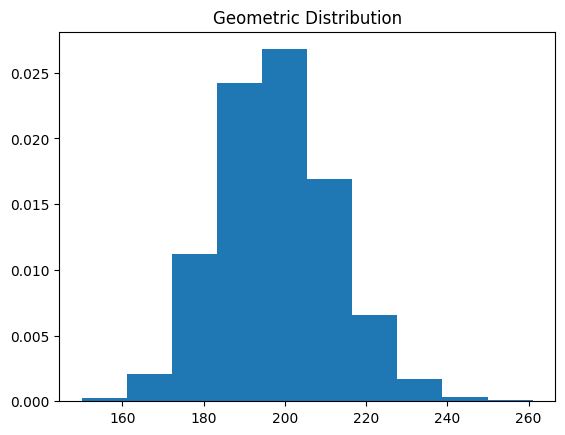
観察結果

お互いに独立な確率変数の数 $N$ が高いほど、正規分布に近づくことを確認でき、中心極限定理の妥当性を理解できました。

---

結論と考察

主要な発見

1. 正規分布の再生性: 独立な正規分布の和は再び正規分布に従う
2. 中心極限定理の実証: 元の分布の形状に関わらず、独立同分布の和は正規分布に収束する
3. 収束の速度: $N$ が増加するにつれて、より明確に正規分布の特徴（釣り鐘型）が現れる

実用的な意義

中心極限定理は以下の分野で重要な役割を果たします：

• 統計的推定: 標本平均の分布が分かることで、母集団パラメータの推定が可能
• 品質管理: 製品の品質指標の分布予測
• 金融工学: リスク管理とポートフォリオ理論
• 実験科学: 測定誤差の統計的処理

数学的補足

中心極限定理の厳密な表現：

$\frac{\bar{X}_n - μ}{\frac{σ}{\sqrt{n}}} \xrightarrow{d} N(0,1) \quad (n \to \infty)$

ここで、$\xrightarrow{d}$ は分布収束を表します。

実践的なヒント

• サンプルサイズ: 一般的に $n \geq 30$ で中心極限定理の効果が顕著に現れる
• 分布の形状: 元の分布が極端に歪んでいる場合、より大きな $n$ が必要
• 独立性の仮定: 確率変数間の独立性が重要な前提条件

注意点

中心極限定理が適用できない場合：

• コーシー分布のように分散が無限大の分布
• 確率変数が独立でない場合
• 同一分布でない場合（ただし、リンデベルグ条件下では一般化可能）

次のステップ

中心極限定理の理解を深めるための学習項目：

1. 大数の法則: 標本平均の収束性について
2. 信頼区間: 中心極限定理を用いた区間推定
3. 仮説検定: Z検定とt検定の理論的背景
4. ベリー・エッセーン定理: 収束の速度に関する定量的評価