2.1 連続時間信号のサンプリングとサンプリング定理
基本定義
- T: サンプリング周期
- ωs: サンプリング角周波数
1. 連続時間信号のサンプリング(サンプル値信号・離散時間信号)
xp(t)=x(t)p(t)=n=−∞∑∞x(nT)δ(t−nT)
インパルス列(サンプリング関数)
p(t)=n=−∞∑∞δ(t−nT)
インパルス列は周期関数なので、その複素フーリエ級数は:
ck=T1∫−T/2T/2δ(t)e−jT2πktdt
p(t)=k=−∞∑∞ckejT2πkt=k=−∞∑∞T1ejT2πkt
フーリエ変換すると:
P(ω)=∫−∞∞k=−∞∑∞T1ejT2πkte−jωtdt=k=−∞∑∞T1∫−∞∞e−j(ω−kωs)tdt
デルタ関数のフーリエ変換により:
δ(ω)=2π1∫−∞∞ejωtdt
よって(デルタ関数は偶関数):
P(ω)=T2πk=−∞∑∞δ(kωs−ω)=T2πk=−∞∑∞δ(ω−kωs)
ただし、ωs=T2π
2. サンプル値信号のフーリエ変換
Xp(ω)=F[xp(t)]=2π1[X(ω)∗P(ω)]
[X(ω)∗P(ω)]: 畳み込み
τ=ω−kωsのとき、デルタ関数が1である。よって:
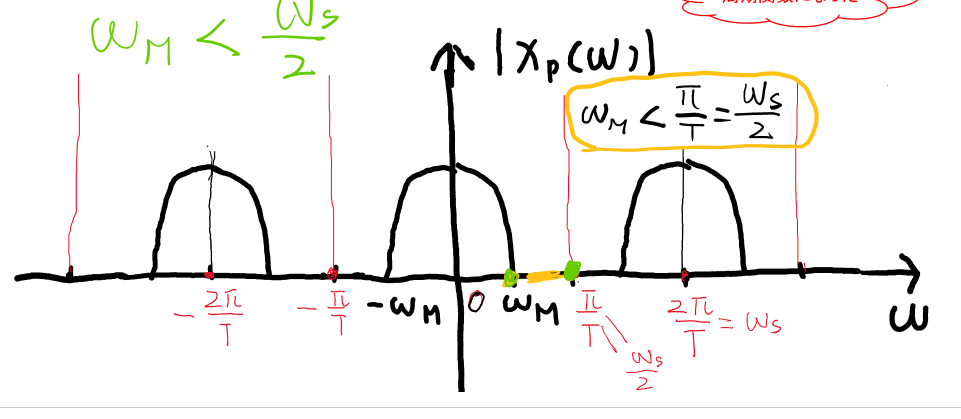
Xp(ω)=T1k=−∞∑∞X(ω−kωs)
ただし、ωs=2π/T(サンプリング角周波数)
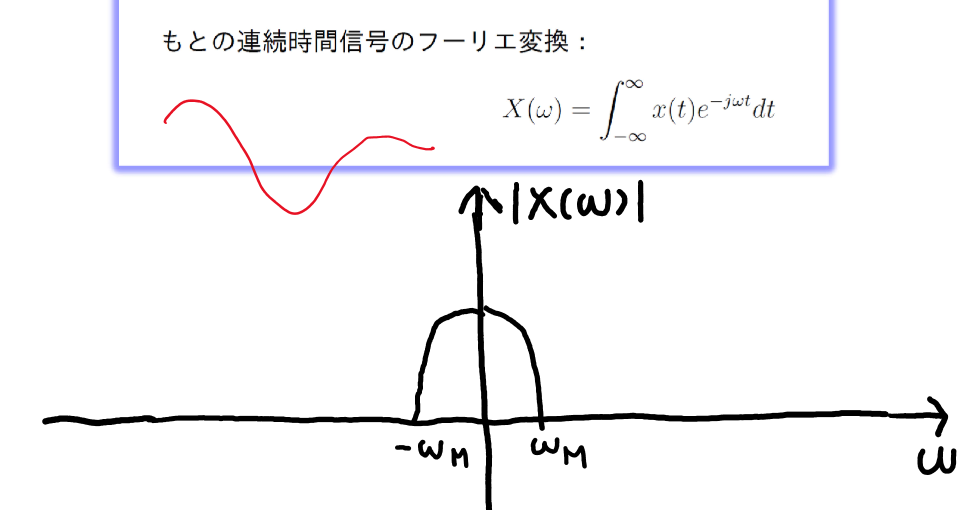
- 横軸: 周波数
- 縦軸: 振幅
- ∣X(ω)∣2: 信号のエネルギー
- 各周波数成分の信号の強さがわかる
フーリエ変換の畳み込み積分の性質

サンプリング定理(ナイキスト-シャノンのサンプリング定理)
信号の最大周波数成分 ωM<ωs/2 のとき、x(t) は x(nT) から完全に回復できる。
- ωM: 信号成分の最大角周波数
周期関数がお互いに干渉しないことを確保する条件。サンプリング定理の条件を満たさない場合、周期関数がお互いに干渉し、その干渉をエイリアシングという。
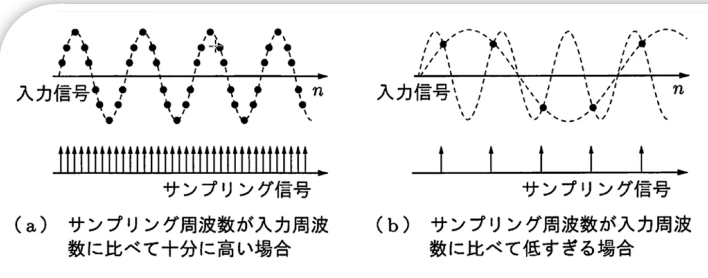
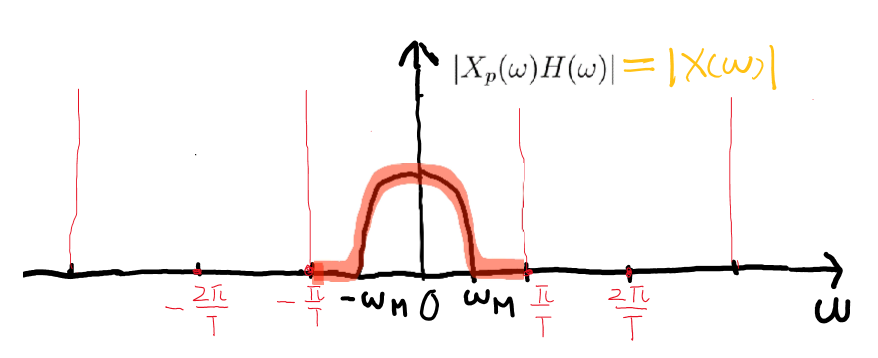
3. 信号の回復(補間)
ゲート関数
H(ω)={T0∣ω∣≤2ωsotherwise
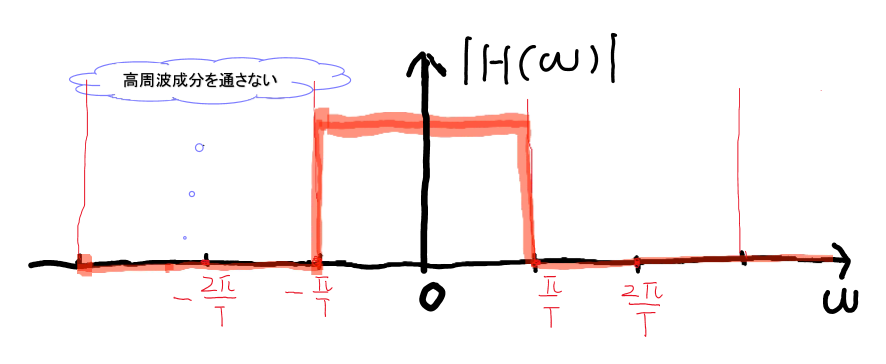
逆フーリエ変換すると:
h(t)=(2ωst)sin(2ωst)
ただし、ωs/2=π/T
X(ω)=XP(ω)H(ω)
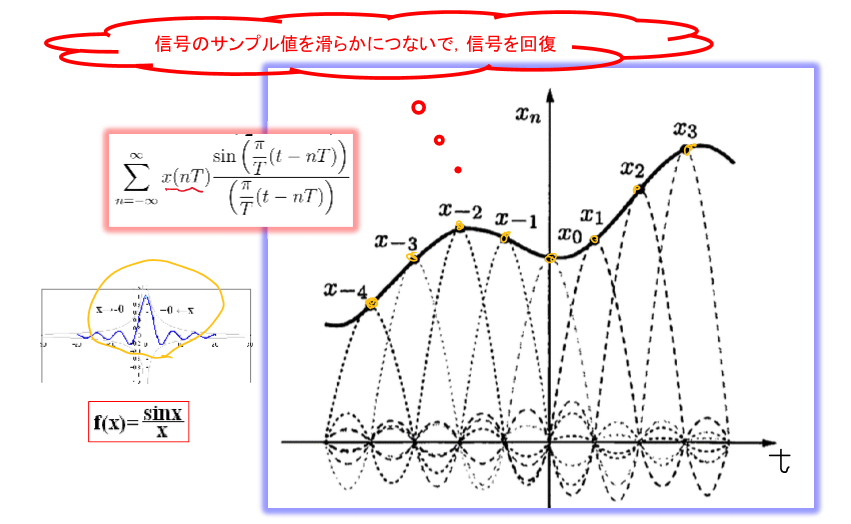
回復の公式
フーリエ変換の畳み込み積分で回復:
x(t)=∫−∞∞xp(τ)h(t−τ)dτ=∫−∞∞[n=−∞∑∞x(nT)δ(τ−nT)]h(t−τ)dτ=n=−∞∑∞x(nT)h(t−nT)=n=−∞∑∞x(nT)(2ωs(t−nT))sin(2ωs(t−nT))=n=−∞∑∞x(nT)(Tπ(t−nT))sin(Tπ(t−nT))
2.2 Z変換
2.2.1 離散時間信号
離散時間信号
x(n)=k=−∞∑∞x(k)δ(n−k)
(離散インパルス信号で表現)
離散インパルス信号
δ(n)={10(n=0)(n=0)
離散ステップ信号
u(n)=k=0∑∞δ(n−k)={10n≥0n<0
離散ステップ信号と離散インパルス信号の関係
δ(n)=u(n)−u(n−1)
2.2.2 Z変換
離散時間信号に対して、ラプラス変換すると z=esT
片側Z変換
X(z)=n=0∑∞x(n)z−n
ただし、z=e(σ+jω)T=esT
収束条件
∣X(z)∣≤n=0∑∞∣x(n)∣r−n
z=rejωTのとき、r−n=rn1:
- r>1: limn→∞r−n→0
- r<1のとき: limn→∞r−n→∞
逆Z変換
x(n)=2πj1∫CX(z)zn−1dz
周回積分路Cはzの収束領域内に取る(あまり使わない)。
主要な性質:
2.3 線形定係数差分方程式による離散時間システムの表現
2.3.1 差分方程式
y(n)+k=1∑Naky(n−k)=k=0∑Mbku(n−k)
2.4 離散時間モデルの伝達関数
差分方程式のZ変換
Y(z)+k=1∑NakY(z)z−k=k=0∑MbkU(z)z−k
伝達関数モデル表現
H(z)=U(z)Y(z)=1+∑k=1Nakz−k∑k=0Mbkz−k=A(z−1)B(z−1)
インパルス応答(畳み込み表現)
y(n)=k=0∑nu(k)h(n−k)=k=0∑nu(n−k)h(k)≈k=0∑Nu(n−k)h(k)
安定なシステムなら、時間が十分たつとh(k)が減衰する。h(k)≈0,k>N
インパルス応答のZ変換は、離散時間システムの伝達関数である。
2.5 離散時間モデルの安定性と周波数応答
2.5.1 離散時間モデルの安定性
伝達関数H(z)の極が**半径1の円(単位円)**内にあれば安定。
- 円周上にある単根: 安定限界
- 単位円の外にある: 不安定
1−αz−11:∣α∣<1
2.5.2 離散時間モデルの周波数応答
H(z)について、z→ejωTを代入する。
ただし、ω∈[0,π/T)
2.6 連続時間モデルから離散時間モデルの導出
2.6.1 インパルス不変の方法
H(z)=n=0∑∞g(n)z−n
2.6.2 微分方程式の近似

前進差分(前進矩形微分)
s=Tz−1,s−1=z−1T
sf(n)=Tf(n+1)−f(n),s−1f(n+1)=s−1f(n)+Tf(n)
後退差分(後退矩形微分)
s=T1−z−1,s−1=1−z−1T
sf(n)=Tf(n)−f(n−1),s−1f(n)=s−1f(n−1)+Tf(n)
双一次変換法(台形積分)
s=T21+z−11−z−1,s−1=2T1−z−11+z−1
2sf(n)+sf(n−1)=Tf(n)−f(n−1),s−1f(n)=s−1f(n−1)+2T[f(n)+f(n−1)]
2.7 フーリエ級数、フーリエ変換とZ変換の関係
2.7.1 フーリエ級数
周期関数の周期信号を扱う。複数の三角関数で信号関数を表現。
ベクトルの内積の視点から見ると、ベクトルを二つの基底ベクトルの線形結合で表される。よって、ある関数を正弦波と余弦波の線形結合で表される。
フーリエ級数
x(t)=2a0+n=1∑∞(ancosnω0t+bnsinnω0t)
係数の計算
an=P2∫0Px(t)cosnω0tdt,bn=P2∫0Px(t)sinnω0tdt
直交性(関数の内積の特性)
P2∫0Pcosmω0tcosnω0tdt=δmn
P2∫0Psinmω0tsinnω0tdt=δmn
P2∫0Psinmω0tcosnω0tdt=0
クロネッカのデルタ
δmn={10m=nm=n
パーセバルの等式
P2∫0Px2(t)dt=2a02+n=1∑∞(an2+bn2)
複素数表現
オイラーの公式により:
ejω0t=cosω0t+jsinω0t
cosω0t=2ejω0t+e−jω0t,sinω0t=2jejω0t−e−jω0t
複素フーリエ級数:
x(t)=n=−∞∑∞cnejnω0t
cn=P1∫0Px(t)e−jnω0tdt
複素数の内積
P1∫0Pejmω0te−jnω0tdt=δmn
パーセバルの等式(複素形式)
P1∫0P∣x(t)∣2dt=n=−∞∑∞∣cn∣2
2.7.2 連続時間フーリエ変換
非周期信号を扱うとき、P→∞
非周期信号を周期無限大の周期関数として扱い、フーリエ級数を適用するとフーリエ変換になる。時間領域から周波数領域への変換が可能。
フーリエ変換が発散するとき(X(ω)=∞)、ラプラス変換を導入する。jωをs=σ+jωで置き換えて取り扱う(σ>0)。
2.7.3 離散時間フーリエ変換
時間だけを離散化する。
2.7.4 離散フーリエ変換
時間と周波数を離散化する。
まとめ
本章では以下の重要な概念を学習した:
- サンプリング定理: 信号の完全な復元に必要な条件
- Z変換: 離散時間システムの解析手法
- 離散時間システム: 差分方程式による表現と安定性
- 連続・離散変換: 各種近似手法の特性
- フーリエ解析: 周波数領域での信号表現
これらの理論はシステム同定における信号処理と離散時間システム解析の基礎となる。






