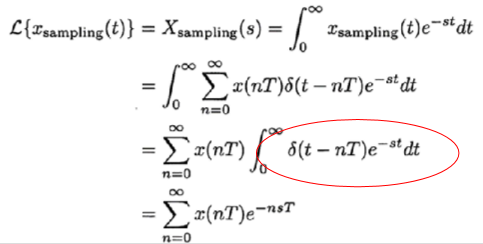メインコンテンツまでスキップ

Z変換

Z変換は、離散時間信号を解析するための数学的手法で、ラプラス変換の離散時間版として位置づけられます。ディジタル信号処理や離散時間制御システムの解析において極めて重要な役割を果たします。

基本定義​

Z変換の定義：

X(z)=Z{x(nT)}=∑n=0∞x(nT)z−nX(z) = \mathcal{Z}\{x(nT)\} = \sum_{n=0}^{\infty}x(nT)z^{-n}

ここで：

  • x(nT)x(nT)：離散時間信号（サンプリング周期 TT）
  • zz：複素変数
  • nn：離散時間インデックス

ラプラス変換からZ変換への導出​

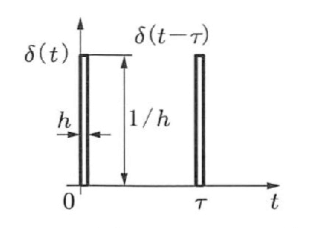
デルタ関数の理解​

ディラックのデルタ関数は、空間の一点にだけ存在する粒子を数式で表現するためにディラックによって発明された関数です。インパルス関数とも呼ばれます。

δ(x)={∞(x=0)0(x≠0)\delta(x) = \begin{cases} \infty & (x = 0) \\ 0 & (x \neq 0) \end{cases}

基本性質： ∫−∞∞δ(x)dx=1\int_{-\infty}^{\infty} \delta(x) dx = 1

選択性質： ∫−∞∞f(x)δ(x)dx=f(0)\int_{-\infty}^{\infty} f(x)\delta(x) dx = f(0)

デルタ関数の物理的意味

ハンマーの一撃のように、ある一点において密度は無限大だが、全体の積分は有限量となる特殊な関数です。

サンプリング過程​

サンプリング（離散化、標本化）は、アナログ信号から時間間隔 TT 秒ごとの信号値を取得する過程です。

  • TT：サンプリング間隔
  • 1/T1/T：サンプリング周波数（1秒あたりのサンプリング回数）
  • サンプル値信号：得られた離散時間信号

サンプリング過程

特定の時刻の信号を取り出す操作： ∫−∞∞f(t)δ(t−τ)dt=f(τ)\int_{-\infty}^{\infty} f(t)\delta(t-\tau)dt = f(\tau)

サンプル値信号（離散時間信号）： xsample(t)=∑n=0∞x(nT)δ(t−nT)x_{\text{sample}}(t) = \sum_{n=0}^{\infty}x(nT)\delta(t-nT)

Z変換の導出​

サンプル値信号にラプラス変換を適用すると：

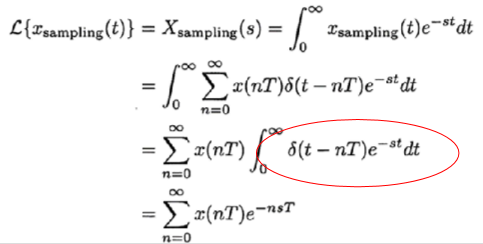
ラプラス変換からZ変換

ここで、z=esT=ejωTz = e^{sT} = e^{j\omega T} （s=jωs = j\omega）と置換すると：

Xsample(s)=X(z)=Z{x(nT)}=∑n=0∞x(nT)z−nX_{\text{sample}}(s) = X(z) = \mathcal{Z}\{x(nT)\} = \sum_{n=0}^{\infty}x(nT)z^{-n}

これがZ変換です。

基本的なZ変換例​

離散時間インパルス関数​

Z{δ(n)}=δ(0)=1\mathcal{Z}\{\delta(n)\} = \delta(0) = 1

離散時間単位ステップ関数​

Z{u(n)}=1+z−1+z−2+z−3+⋯=11−z−1=zz−1\mathcal{Z}\{u(n)\} = 1 + z^{-1} + z^{-2} + z^{-3} + \cdots = \frac{1}{1-z^{-1}} = \frac{z}{z-1}

（等比数列の和による）

等比数列​

x(n)=anx(n) = a^n のZ変換：

Z{an}=1+az−1+a2z−2+a3z−3+⋯=11−az−1=zz−a\mathcal{Z}\{a^n\} = 1 + az^{-1} + a^2z^{-2} + a^3z^{-3} + \cdots = \frac{1}{1-az^{-1}} = \frac{z}{z-a}

線形関数​

x(n)=nx(n) = n のZ変換：

Z{n}=0+z−1+2z−2+3z−3+⋯\mathcal{Z}\{n\} = 0 + z^{-1} + 2z^{-2} + 3z^{-3} + \cdots

漸化式を用いて計算できます：

線形関数のZ変換

三角関数​

  • x(n)=cos⁡(nωT)x(n) = \cos(n\omega T) のZ変換
  • x(n)=sin⁡(nωT)x(n) = \sin(n\omega T) のZ変換

これらも基本的なZ変換表から求めることができます。

Z変換の性質​

Z変換は以下の重要な性質を持ちます：

数学的意味の違い
  • ラプラス変換の ss：微分の意味（微分方程式）
  • Z変換の zz：時間推移の意味（差分方程式）

1. 線形性（Linearity）​

Z[ax1(nT)+bx2(nT)]=aZ[x1(nT)]+bZ[x2(nT)]\mathcal{Z}[ax_1(nT) + bx_2(nT)] = a\mathcal{Z}[x_1(nT)] + b\mathcal{Z}[x_2(nT)]

2. 時間推移​

a) 前移（時間進み）： Z[x(nT+mT)]=zm{X(z)−∑n=0m−1x(nT)z−n}\mathcal{Z}[x(nT+mT)] = z^m\left\{X(z) - \sum_{n=0}^{m-1} x(nT)z^{-n}\right\}

b) 後移（時間遅れ）： Z[x(nT−mT)]=z−mX(z)\mathcal{Z}[x(nT-mT)] = z^{-m}X(z)

遅延演算子

X(z)X(z) に z−1z^{-1} が掛けられると、信号は1サンプル分遅延します。z−1z^{-1} は遅延演算子として機能します。

3. 指数による乗算​

Z[anx(nT)]=X(a−1z)\mathcal{Z}[a^n x(nT)] = X(a^{-1}z)

4. 微分​

Z[nT⋅x(nT)]=−TzdX(z)dz\mathcal{Z}[nT \cdot x(nT)] = -Tz\frac{dX(z)}{dz}

5. 畳み込み定理​

Y(z)=Z[∑k=0∞x(kT)h(nT−kT)]=X(z)H(z)Y(z) = \mathcal{Z}\left[\sum_{k=0}^{\infty} x(kT)h(nT-kT)\right] = X(z)H(z)

時間領域での畳み込みが、Z領域では単純な乗算になります。

6. 初期値定理​

x(0)=lim⁡z→∞X(z)x(0) = \lim_{z \to \infty} X(z)

7. 最終値定理​

lim⁡n→∞x(nT)=lim⁡z→1(1−z−1)X(z)\lim_{n \to \infty} x(nT) = \lim_{z \to 1} (1-z^{-1})X(z)

逆Z変換​

逆Z変換は、基本的なZ変換対と部分分数展開（留数法）を用いて求めます。

基本的な逆変換​

基本のZ変換対： Z[an]=zz−a\mathcal{Z}[a^n] = \frac{z}{z-a}

部分分数展開​

一般的なZ変換を部分分数に展開：

X(z)=c1zz−a1+c2zz−a2+c3zz−a3+⋯X(z) = c_1\frac{z}{z-a_1} + c_2\frac{z}{z-a_2} + c_3\frac{z}{z-a_3} + \cdots

これにより、逆Z変換は：

x(n)=c1a1n+c2a2n+c3a3n+⋯(n≥0)x(n) = c_1a_1^n + c_2a_2^n + c_3a_3^n + \cdots \quad (n \geq 0)

実用的な計算

実際の逆Z変換では、部分分数展開とZ変換表を組み合わせて使用することが一般的です。

Z変換表​

主要な関数のZ変換：

Z変換表

基本的なZ変換対​

離散時間関数 x(n)x(n)Z変換 X(z)X(z)収束領域
δ(n)\delta(n)11全平面
u(n)u(n)zz−1\frac{z}{z-1}$
anu(n)a^n u(n)zz−a\frac{z}{z-a}$
nanu(n)na^n u(n)az(z−a)2\frac{az}{(z-a)^2}$
cos⁡(nωT)u(n)\cos(n\omega T)u(n)z(z−cos⁡ωT)z2−2zcos⁡ωT+1\frac{z(z-\cos\omega T)}{z^2-2z\cos\omega T+1}$
sin⁡(nωT)u(n)\sin(n\omega T)u(n)zsin⁡ωTz2−2zcos⁡ωT+1\frac{z\sin\omega T}{z^2-2z\cos\omega T+1}$

工学的応用​

離散時間システム解析​

Z変換により、離散時間システムの入出力関係を伝達関数で表現：

H(z)=Y(z)X(z)H(z) = \frac{Y(z)}{X(z)}

差分方程式の解法​

線形差分方程式をZ変換により代数方程式に変換して解くことができます。

ディジタルフィルタ設計​

  • FIRフィルタ：有限インパルス応答フィルタ
  • IIRフィルタ：無限インパルス応答フィルタ

安定性解析​

システムの安定性は、伝達関数の極の位置で判定：

  • 単位円内：安定
  • 単位円外：不安定

まとめ​

Z変換は離散時間信号処理の基礎となる重要なツールです：

  1. 離散化：連続時間信号の離散化とサンプリング理論
  2. 変換対：時間領域と周波数領域の関係
  3. システム解析：離散時間システムの数学的表現
  4. 実用性：ディジタル信号処理とディジタル制御への応用

次章では、離散フーリエ変換について学習し、実際のディジタル信号処理での実装について詳しく見ていきます。

次のステップ
  • 離散フーリエ変換（DFT）：実際の計算で使用される変換
  • 高速フーリエ変換（FFT）：効率的な計算アルゴリズム
  • ディジタルフィルタ：FIRフィルタとIIRフィルタの設計
  • 離散時間システム：システム解析と制御理論への応用