PID制御器のシミュレーション

制御対象

4次の伝達関数で表される制御対象を考える：

$$G(s)=\frac{12s+8}{20s^4+112s^3+147s^2+62s+8}$$

状態空間表現への変換

num = [0 0 12 8];
den = [20 113 147 62 8];
sysg = tf(num, den);                    % 伝達関数
[Ao,Bo,Co,Do] = tf2ss(num,den);        % 状態空間表現への変換

PID制御器

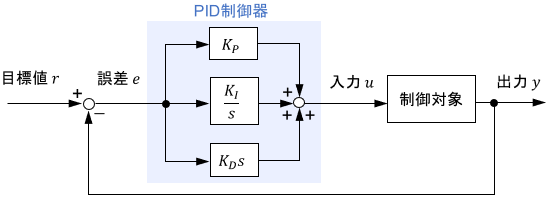
離散時間での表現（$k \to n$）：

$$e(n)=r(n)-y(n-1)$$

偏差の定義

偏差 = 目標値 - 一個前の制御量

$$U(z)=E(z)C(z)$$

PID制御器伝達関数

$$C(s)=c_p+c_i\frac{1}{s}+c_d\frac{s}{\gamma s+1}, \quad \gamma=4\times T$$

gamma = 4*T;  % γ（微分項のフィルタ時定数）
cp = 6;       % 比例ゲイン
ci = 1;       % 積分ゲイン  
cd = 7;       % 微分ゲイン

数値積分手法による離散化

1. 前進差分

PID制御器のZ変換表現

$$C(z)=c_p+c_i\frac{Tz^{-1}}{1-z^{-1}}+c_d\frac{1-z^{-1}}{\gamma+(T-\gamma)z^{-1}}$$

P-I-D分解実装（推奨方法）

比例制御（P）：

$$u_p(n)=c_pe(n)$$

積分制御（I）：

$$u_i(n)-u_i(n-1)=c_iTe(n-1) \Rightarrow u_i(n)=u_i(n-1)+c_iTe(n-1)$$

積分制御の意味

偏差の累積で制御する

微分制御（D）：

$$\gamma u_d(n)+(T-\gamma)u_d(n-1)=c_d(e(n)-e(n-1))$$ $$\Rightarrow u_d(n)=\frac{c_d}{\gamma}\left(e(n)-e(n-1)-\frac{T-\gamma}{\gamma}u_d(n-1)\right)$$

微分制御の意味

偏差の変化で制御するつもりだが、初期状態には変化がない。微分の$s$ × ローパスフィルタ$\frac{1}{\gamma s+1}$

状態空間表現（前進差分）

$$x(n+1)=x(n)+T(Ax(n)+bu(n))$$ $$y(n)=Cx(n)+Du(n)$$

2. 後退差分

PID制御器のZ変換表現

$$C(z)=c_p+c_i\frac{T}{1-z^{-1}}+c_d\frac{1-z^{-1}}{\gamma(1-z^{-1})+T}$$

P-I-D分解実装

比例制御（P）：

$$u_p(n)=c_pe(n)$$

積分制御（I）：

$$u_i(n)-u_i(n-1)=c_iTe(n) \Rightarrow u_i(n)=c_iTe(n)+u_i(n-1)$$

微分制御（D）：

$$(\gamma+T)u_d(n)-\gamma u_d(n-1)=c_d(e(n)-e(n-1))$$ $$\Rightarrow u_d(n)=\frac{c_d(e(n)-e(n-1)) +\gamma u_d(n-1)}{(\gamma+T)}$$

状態空間表現（後退差分）

$$x(n)-x(n-1)=T(Ax(n)+bu(n)) \Rightarrow x(n)=(I-TA)^{-1}(x(n-1)+Tbu(n))$$ $$y(n)=Cx(n)+Du(n)$$

3. 双一次変換法

PID制御器のZ変換表現

$$\begin{aligned} C(z)&=c_p+c_i\frac{T}{2}\frac{1+z^{-1}}{1-z^{-1}}+c_d\frac{1}{\gamma+\frac{T(1+z^{-1})}{2(1-z^{-1})}}\\ &=c_p+\frac{Tc_i}{2}\frac{1+z^{-1}}{1-z^{-1}}+2c_d\frac{1-z^{-1}}{2\gamma+T+(T-2\gamma)z^{-1}} \end{aligned}$$

P-I-D分解実装

比例制御（P）：

$$u_p(n)=c_pe(n)$$

積分制御（I）：

$$u_i(n)-u_i(n-1)=\frac{c_iT}{2}(e(n)+e(n-1)) \Rightarrow u_i(n)=\frac{c_iT}{2}(e(n)+e(n-1))+u_i(n-1)$$

微分制御（D）：

$$(2\gamma+T)u_d(n)+(T-2\gamma)u_d(n-1)=2c_d(e(n)-e(n-1))$$ $$\Rightarrow u_d(n)= \frac{2c_d(e(n)-e(n-1))+(2\gamma-T)u_d(n-1)}{2\gamma+T}$$

状態空間表現（双一次変換）

$$\frac{2}{T}(x(n)-x(n-1))=A(x(n)+x(n-1))+b(u(n)+u(n-1))$$ $$\Rightarrow x(n)=(2I-TA)^{-1}[(2I+AT)x(n-1)+bT(u(n)+u(n-1))]$$ $$y(n)=Cx(n)+Du(n)$$

MATLABシミュレーションコード

プログラミング上の注意点

行列計算の注意事項

行列計算する時、行列の次元に注意

inv()  % 逆行列
eye()  % 単位行列I
./     % 行列除算
.*     % 行列要素ごとの乗算

最も注意すべきなのは、括弧と正負の符号である。理由は、コードの数式が読みづらい。

解決策：

1. コードをLaTeX公式に入れて、確認する
2. 目と手でもう一回計算して確認する

制御ループの実装

for k=1:N+1
    y(k) = C*x(k) + D*u(k)     % 出力計算
    e(k) = r(k) - y(k)         % 偏差計算
    
    % 離散方法
    up(k) = ...                % 比例制御
    ui(k) = ...                % 積分制御  
    ud(k) = ...                % 微分制御
    u(k) = up(k) + ui(k) + ud(k)
    
    % 前進差分で状態更新
    x(k+1) = x(k) + T*(A*x(k) + B*u(k))
end

制御順序の重要性

1. 実際の場合、センサからの観測値をもらうので、$y(t)$が先の方である
2. しかし、$y(t)$を先にすると、$y=Cx+Du$における$u$がずっと0で計算している。普通に$D=0$なので影響がない
3. また、現在の入力$u(t)$を求めたい。$u(t)$を求めるために、現在の出力（観察値）$y(t)$が必要である。出力を得るために、現在まだ求めていない入力を使うべきではない

完全なシミュレーションコード

PID制御器比較

clear
close all
set(0,'DefaultAxesFontName','Times New Roman')
set(0,'DefaultAxesFontSize',22)

%--------------------------------------------------------------------
%  同定ゼミ宿題 PID制御器のシミュレーション
%                                                5/26 by YANG
%---------------------------------------------------------------------

Tmax = 30;    % シミュレーション時間
T = 0.05;     % サンプリング周期
n = Tmax/T;   % サンプル数
gamma = 4*T;  % フィルタ時定数

% PIDパラメータ
cp = 6;       % 比例ゲイン
ci = 1;       % 積分ゲイン
cd = 7;       % 微分ゲイン

% 制御対象
num = [0 0 12 8];
den = [20 113 147 62 8];
sysg = tf(num, den);
[Ao,Bo,Co,Do] = tf2ss(num,den);

% 配列初期化
t = zeros(1, n+1);
r = ones(1, n+1);      % 目標値（ステップ入力）

% 前進差分用配列
upF = zeros(1, n+1);   % P制御入力
uiF = zeros(1, n+1);   % I制御入力
udF = zeros(1, n+1);   % D制御入力
uF = zeros(1, n+1);    % 総制御入力
xF = zeros(4, n+1);    % 状態変数
yF = zeros(1, n+1);    % 出力
eF = zeros(1, n+1);    % 偏差

% 前進差分によるPID制御
for k = 2:n+1
    t(k) = (k-1)*T;
    yF(k) = Co*xF(:,k) + Do*uF(k);
    eF(k) = r(k) - yF(k);
    
    % PID制御計算
    upF(k) = cp*eF(k);
    uiF(k) = uiF(k-1) + ci*T*eF(k-1);
    udF(k) = (cd*(eF(k)-eF(k-1)) - (T-gamma)*udF(k-1))/gamma;
    uF(k) = upF(k) + uiF(k) + udF(k);
    
    % 状態更新
    xF(:,k+1) = xF(:,k) + T*(Ao*xF(:,k) + Bo*uF(k));
end

% 他の手法（後退差分、双一次変換）も同様に実装...

P-I-D個別効果比較

% P, I, D制御の個別効果を比較するシミュレーション
for k = 2:n+1
    t(k) = (k-1)*T;
    
    % P制御のみ
    ypF(k) = Co*xpF(:,k) + Do*up(k);
    epF(k) = r(k) - ypF(k);
    up(k) = cp*epF(k);
    xpF(:,k+1) = xpF(:,k) + T*(Ao*xpF(:,k) + Bo*up(k));
    
    % I制御のみ
    yiF(k) = Co*xiF(:,k) + Do*ui(k);
    eiF(k) = r(k) - yiF(k);
    ui(k) = ui(k-1) + ci*T*eiF(k-1);
    xiF(:,k+1) = xiF(:,k) + T*(Ao*xiF(:,k) + Bo*ui(k));
    
    % D制御のみ
    ydF(k) = Co*xdF(:,k) + Do*ud(k);
    edF(k) = r(k) - ydF(k);
    ud(k) = (cd*(edF(k)-edF(k-1)) - (T-gamma)*ud(k-1))/gamma;
    xdF(:,k+1) = xdF(:,k) + T*(Ao*xdF(:,k) + Bo*ud(k));
end

結果可視化

% 制御入力の比較
subplot(2,1,1); 
plot(t,uF,t,uB,t,uD); 
title('制御入力 u(t)');
legend('前進差分','後退差分','双一次変換'); 
ylabel('u(t)'); 
xlabel('Time[sec]'); 
grid on

% 出力応答の比較
subplot(2,1,2);
plot(t,yF,t,yB,t,yD,t,r,'--'); 
title('目標値r(t)と出力y(t)');
legend('前進差分','後退差分','双一次変換','目標値'); 
ylabel('y(t)'); 
xlabel('Time[sec]'); 
grid on

性能比較と考察

各手法の特性

手法	安定性	精度	計算負荷	実装容易さ
前進差分	条件付き	低	低	高
後退差分	良好	中	中	中
双一次変換	優秀	高	中	中

PID制御の各要素の役割

P制御（比例制御）

• 効果: 偏差に比例した制御
• 特徴: 応答速度の向上、定常偏差の残存
• 調整: ゲインを大きくすると応答が速くなるが、振動しやすくなる

I制御（積分制御）

• 効果: 偏差の累積を解消
• 特徴: 定常偏差の除去、応答の遅れ
• 調整: ゲインを大きくすると定常偏差は早く除去されるが、オーバーシュートが増加

D制御（微分制御）

• 効果: 偏差の変化率に基づく制御
• 特徴: 応答の改善、雑音の増幅
• 調整: ゲインを大きくすると安定性は向上するが、雑音に敏感になる

実装上のポイント

1. ゼロオーダーホールドの適用: 因果関係の保持
2. フォント設定: 可読性の向上
3. 軸ラベルと単位: グラフの明確化
4. 初期値設定: 適切な初期条件の設定

まとめ

本シミュレーションでは：

1. 離散化手法: 3つの数値積分手法による比較
2. PID制御: 各制御要素の個別効果と統合効果
3. 実装技法: MATLABによる効率的なプログラミング手法
4. 性能評価: 安定性、精度、実用性の観点からの評価

これらの知識は、実際の制御系設計における重要な基盤となる。特に、離散化手法の選択は制御性能に大きく影響するため、システムの特性と要求性能に応じた適切な選択が重要である。