凸最適化理論

概要

凸最適化は最適化理論における最も重要な分野の一つです。凸性という特別な性質により、局所最適解が大域最適解となることが保証され、効率的なアルゴリズムが存在します。

凸集合（Convex Set）

定義と基本性質

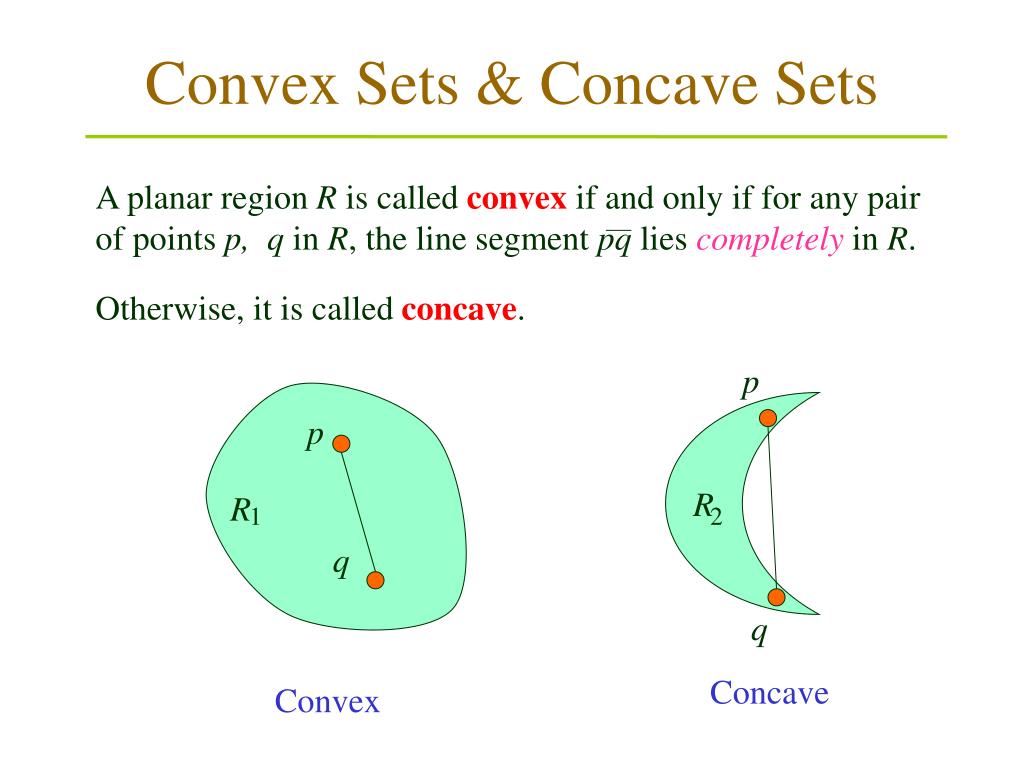
凸集合の定義: 任意の2点 $x, y$ を含む集合 $C$ に対して、線分 $\lambda x + (1 - \lambda)y$ （$0 \leq \lambda \leq 1$）も集合内に含まれるとき、集合 $C$ を凸集合と呼びます。

$$x, y \in C, \quad 0 \leq \lambda \leq 1 \Rightarrow \lambda x + (1-\lambda)y \in C$$

直感的理解

凸集合は「内側に向かって凹んでいない」集合です。集合内の任意の2点を結ぶ直線が完全に集合内に収まります。

凸集合の例

基本的な例

• ユークリッド空間の球: $\{x \in \mathbb{R}^n : \|x - x_0\| \leq r\}$
• 直方体（超立方体）: $\{x \in \mathbb{R}^n : a_i \leq x_i \leq b_i, i = 1,\ldots,n\}$
• 半空間: $\{x \in \mathbb{R}^n : a^T x \leq b\}$
• アフィン集合: $\{x \in \mathbb{R}^n : Ax = b\}$

重要な性質

1. 凸集合の交集合は凸集合
2. 凸集合のアフィン変換は凸集合
3. 凸集合の凸結合は凸集合

数学的な厳密性

凸集合の定義は線形結合の概念と密接に関連しています。$\lambda + (1-\lambda) = 1$ という制約により、2点間の「内挿」が表現されます。

凸包（Convex Hull）

集合 $S$ の凸包 $\text{conv}(S)$ は、$S$ を含む最小の凸集合です：

$$\text{conv}(S) = \left\{\sum_{i=1}^k \lambda_i x_i : x_i \in S, \lambda_i \geq 0, \sum_{i=1}^k \lambda_i = 1\right\}$$

凸関数（Convex Function）

定義

関数 $f(x)$ が凸集合 $\text{dom}(f)$ 上で定義されていて、以下の条件を満たすとき、$f$ を凸関数と呼びます：

$$f(\lambda x + (1 - \lambda)y) \leq \lambda f(x) + (1 - \lambda)f(y)$$

すべての $x, y \in \text{dom}(f)$ および $0 \leq \lambda \leq 1$ に対して成り立ちます。

幾何学的解釈

凸関数のグラフは「上に膨らむ」形状を持ち、任意の2点を結ぶ線分が常にグラフの上側に位置します。

凸関数の例

基本的な例

1. 二次関数: $f(x) = x^2$ （$\mathbb{R}$ 上）
2. 指数関数: $f(x) = e^x$ （$\mathbb{R}$ 上）
3. 絶対値関数: $f(x) = |x|$ （$\mathbb{R}$ 上）
4. ノルム関数: $f(x) = \|x\|_p$ （$p \geq 1$）
5. 二次形式: $f(x) = x^T Q x$ （$Q \succeq 0$）

合成による凸関数の構成

• 正の線形結合: $\alpha f + \beta g$ （$\alpha, \beta \geq 0$）
• 最大値: $f(x) = \max\{f_1(x), f_2(x)\}$
• 合成関数: 特定の条件下での合成

凸関数の判定法

一次条件（勾配条件）

$f$ が微分可能な場合、以下が成り立つとき $f$ は凸関数：

$$f(y) \geq f(x) + \nabla f(x)^T (y - x), \quad \forall x, y \in \text{dom}(f)$$

この条件は、接線が関数の下界となることを示します。

二次条件（ヘッセ行列条件）

$f$ が二回微分可能な場合、以下が成り立つとき $f$ は凸関数：

$$\nabla^2 f(x) \succeq 0, \quad \forall x \in \text{dom}(f)$$

ここで $\nabla^2 f(x)$ はヘッセ行列（二次微分行列）です。

厳密凸性

$\nabla^2 f(x) \succ 0$ （正定値）の場合、$f$ は厳密凸関数となり、最適解が一意に決まります。

凸計画問題（Convex Optimization Problem）

定義

目的関数が凸関数で、制約条件が凸集合で表される最適化問題を凸計画問題と呼びます：

$$\begin{align} \min_x \quad & f(x) \\ \text{subject to} \quad & x \in C \end{align}$$

ここで：

• $f(x)$ は凸関数（目的関数）
• $C$ は凸集合（制約集合）

標準形

より一般的な凸計画問題の標準形は以下のように表現されます：

$$\begin{align} \min_x \quad & f_0(x) \\ \text{subject to} \quad & f_i(x) \leq 0, \quad i = 1, \ldots, m \\ & h_j(x) = 0, \quad j = 1, \ldots, p \end{align}$$

ここで：

• $f_0, f_1, \ldots, f_m$ は凸関数
• $h_1, \ldots, h_p$ はアフィン関数（$h_j(x) = a_j^T x - b_j$）

凸最適化の基本定理

定理: 凸計画問題において、局所最適解は大域最適解である。

証明のアイデア: 局所最適解 $x^*$ が大域最適解でないと仮定すると、より良い点 $y$ が存在する。凸性により、$x^*$ と $y$ を結ぶ線分上の点で $x^*$ より良い目的関数値を持つ点が $x^*$ の近傍に存在し、局所最適性に矛盾。

凸最適化の威力

この定理により、凸問題では局所探索アルゴリズムで大域最適解を求めることができます。

典型的な凸計画問題

線形計画問題（LP: Linear Programming）

$$\begin{align} \min_x \quad & c^T x \\ \text{subject to} \quad & Ax \leq b \\ & Ex = d \end{align}$$

二次計画問題（QP: Quadratic Programming）

$$\begin{align} \min_x \quad & \frac{1}{2}x^T Q x + c^T x \\ \text{subject to} \quad & Ax \leq b \\ & Ex = d \end{align}$$

ここで $Q \succeq 0$

LASSO回帰

$$\min_x \quad \frac{1}{2}\|Ax - b\|_2^2 + \lambda \|x\|_1$$

解法アルゴリズム

内点法（Interior Point Methods）

• 多項式時間アルゴリズム
• 大規模問題に有効
• 制約の内部を通る経路で最適解に収束

勾配法

• 単純で実装が容易
• 収束速度は線形
• 大規模問題での並列化が可能

近接勾配法（Proximal Gradient Methods）

• 非平滑凸関数に対応
• 構造を利用した効率的な解法
• 機械学習での応用が広い

双対理論

ラグランジュ双対

凸計画問題のラグランジュ関数は以下で定義されます：

$$L(x, \lambda, \nu) = f_0(x) + \sum_{i=1}^m \lambda_i f_i(x) + \sum_{j=1}^p \nu_j h_j(x)$$

双対関数は：

$$g(\lambda, \nu) = \inf_x L(x, \lambda, \nu)$$

双対問題

元の問題（主問題）に対する双対問題は：

$$\begin{align} \max_{\lambda, \nu} \quad & g(\lambda, \nu) \\ \text{subject to} \quad & \lambda \geq 0 \end{align}$$

強双対性

凸問題では、適当な制約想定（スレーター条件など）の下で強双対性が成り立ちます：

$$\text{主問題の最適値} = \text{双対問題の最適値}$$

実践的意義

双対理論は最適性条件の導出、アルゴリズムの設計、感度解析などに重要な役割を果たします。

KKT条件

最適性の必要十分条件

凸計画問題において、点 $x^*$ が最適解であるための必要十分条件はKKT条件（Karush-Kuhn-Tucker条件）です：

1. 停留条件: $\nabla f_0(x^*) + \sum_{i=1}^m \lambda_i^* \nabla f_i(x^*) + \sum_{j=1}^p \nu_j^* \nabla h_j(x^*) = 0$

2. 実行可能性: $f_i(x^*) \leq 0$, $h_j(x^*) = 0$

3. 双対実行可能性: $\lambda_i^* \geq 0$

4. 相補性: $\lambda_i^* f_i(x^*) = 0$

経済学的解釈

• $\lambda_i^*$: 制約 $i$ のシャドウ価格（限界価値）
• 相補性: 制約が有効でない場合、そのシャドウ価格は0

応用例

機械学習での応用

サポートベクターマシン（SVM）

$$\begin{align} \min_{w, b, \xi} \quad & \frac{1}{2}\|w\|^2 + C \sum_{i=1}^n \xi_i \\ \text{subject to} \quad & y_i(w^T x_i + b) \geq 1 - \xi_i \\ & \xi_i \geq 0 \end{align}$$

ロジスティック回帰

$$\min_w \quad \sum_{i=1}^n \log(1 + e^{-y_i w^T x_i}) + \lambda \|w\|_2^2$$

ポートフォリオ最適化

マルコビッツの平均分散モデル

$$\begin{align} \min_x \quad & \frac{1}{2}x^T \Sigma x \\ \text{subject to} \quad & \mu^T x \geq r \\ & \mathbf{1}^T x = 1 \\ & x \geq 0 \end{align}$$

ここで：

• $x$: ポートフォリオウェイト
• $\Sigma$: 共分散行列
• $\mu$: 期待収益率ベクトル
• $r$: 目標収益率

数値解法の実装

Python実装例

import cvxpy as cp
import numpy as np

# 二次計画問題の例
def solve_quadratic_program(Q, c, A, b):
    """
    min (1/2)x^T Q x + c^T x
    s.t. Ax <= b
    """
    n = Q.shape[0]
    x = cp.Variable(n)
    
    objective = cp.Minimize(0.5 * cp.quad_form(x, Q) + c.T @ x)
    constraints = [A @ x <= b]
    
    problem = cp.Problem(objective, constraints)
    problem.solve()
    
    return x.value, problem.value

# LASSO回帰の例
def solve_lasso(A, b, lambda_reg):
    """
    min (1/2)||Ax - b||_2^2 + λ||x||_1
    """
    m, n = A.shape
    x = cp.Variable(n)
    
    objective = cp.Minimize(
        0.5 * cp.sum_squares(A @ x - b) + lambda_reg * cp.norm(x, 1)
    )
    
    problem = cp.Problem(objective)
    problem.solve()
    
    return x.value, problem.value

MATLAB実装例

% 二次計画問題
function [x, fval] = solve_qp_matlab(Q, c, A, b)
    options = optimoptions('quadprog', 'Display', 'off');
    [x, fval] = quadprog(Q, c, A, b, [], [], [], [], [], options);
end

% 線形計画問題
function [x, fval] = solve_lp_matlab(c, A, b)
    options = optimoptions('linprog', 'Display', 'off');
    [x, fval] = linprog(c, A, b, [], [], [], [], options);
end

高度なトピック

半正定値計画（SDP）

半正定値計画問題は凸最適化の重要な拡張です：

$$\begin{align} \min_X \quad & \text{trace}(CX) \\ \text{subject to} \quad & \text{trace}(A_i X) = b_i, \quad i = 1, \ldots, m \\ & X \succeq 0 \end{align}$$

ここで $X \succeq 0$ は $X$ が半正定値行列であることを表します。

錐計画（Conic Programming）

一般的な錐計画問題：

$$\begin{align} \min_x \quad & c^T x \\ \text{subject to} \quad & Ax = b \\ & x \in K \end{align}$$

ここで $K$ は凸錐です。

ロバスト最適化

不確実性を考慮した最適化：

$$\min_x \max_{u \in U} f(x, u)$$

多くの場合、適切な不確実性集合 $U$ の選択により凸問題となります。

まとめ

凸最適化理論の主要なポイント：

1. 凸集合と凸関数の基本概念の理解
2. 局所最適解 = 大域最適解という強力な性質
3. KKT条件による最適性の特徴づけ
4. 双対理論の理論的・実践的重要性
5. 効率的なアルゴリズムの存在
6. 幅広い応用分野での有用性

参考文献

1. Boyd, S., & Vandenberghe, L. (2004). Convex Optimization. Cambridge University Press.
2. Rockafellar, R. T. (1970). Convex Analysis. Princeton University Press.
3. Ben-Tal, A., & Nemirovski, A. (2001). Lectures on Modern Convex Optimization. SIAM.
4. Beck, A. (2017). First-Order Methods in Optimization. SIAM.