境界制約あり最適化問題

Posted Oct 31, 2024

By Guang-Ze Yang 13 min read

3.4 決定変数の境界制約による最適化問題

これまで、理論的な無制約最適化問題が研究されたが、特定の応用分野では「無制約最適化問題」(unconstrained optimization problems)においても、決定変数(decision variable)に制約があることがよくある。これらの問題は、数学的には典型的な無制約最適化問題ではない。したがって、本節では、決定変数の制約(decision variable bounds)による最適化問題について考察する。まず、単変数の最適化問題を扱い、その後に多変数問題の解法が紹介される。

3.4.1 単変数の決定変数の境界制約による最適化問題(fminbnd)

境界制約あり最適問題の定義(3.4)

\[\begin{array}{c} \min_{x\;\textrm{s.t.}x_m \le x\le x_M } f(x) \end{array}\]

ただし、 $x_{m\;}$ と $x_M$ は決定変数制約の下限と上限である。「s. t.」という表記は、「subject to（~に従って）」を意味し、これに続いて制約条件が示される。

MATLABのOptimization Toolboxでは、関数 fminbnd() が用意され、決定変数に制約がある単変数関数の最適化問題を直接解くことができる。関数の構文は以下の通りである。

x = fminbnd(f, xm, xM)

[x, f0, flag, out] = fminbnd(f, xm, xM, options)

構造体変数として最適化問題を記述することも可能:

[x, f0, flag, out] = fminbnd(problem)

`fminbndアルゴリズム：`

MATLAB公式サイト：fminbnd - Find local minimum of single-variable function on fixed interval - MATLAB

fminbnd is a function file. The algorithm is based on golden section search(黄金比検索) and parabolic interpolation(放物線補間).

黄金比検索(golden section search)

Golden-section search - Wikipedia (By ChatGPT)

黄金比検索は、単一変数関数の最小値または最大値を求めるための数値最適化アルゴリズムの一つである。特に、関数が連続であり、評価が非常にコストのかかる場合に有効である。以下の特徴がある。

基本原理:

黄金比（約0.618）の比率を用いて、探索範囲を分割する。これにより、無駄な評価を最小限に抑えつつ、最小値を効率的に求める。
範囲を分割することで、次第に関心のある範囲を狭めていく。

手順:

初期区間を設定し、その区間を黄金比に基づいて2つの点に分ける。
関数の値を評価し、どちらの点がより小さいかを比較する。
より小さい点の近くの部分を次の探索範囲として設定し、再び分割を行う。
このプロセスを、所定の精度（トレランス）に達するまで繰り返す。

利点:

定義された区間内で最適な解を求めるため、グラフの形状に依存せず、良好な収束性を持っている。
機能が連続している限り、評価回数が少なくて済む。

放物線補間(parabolic interpolation):

(By ChatGPT)

放物線補間は、関数の最小値を求めるために、関数の値を用いて放物線を近似する方法である。以下のような特徴がある。

基本原理:

3つの評価点を用いて、それらの点を通る放物線を描く。放物線の頂点が最小値に近いと仮定して、次の探索点を決定する。
放物線の方程式は、2次式（ ${\textrm{ax}}^{\;2} +\textrm{bx}+c$ ）で表される。

手順

初期の3つの点を選択する。これらの点は、評価したい関数の異なる位置での値である。
これらの点を用いて放物線を構築する。
放物線の頂点（最小値を持つ点）を計算し、次の探索点として設定する。
新しい点で関数を評価し、再度放物線を構築していくプロセスを繰り返す。

利点:

放物線の形状を利用するため、勾配が情報として使える場合に特に効果的である。
ゴールデンセクションサーチに比べて、より速く収束することが期待できる。

例題 3.23:

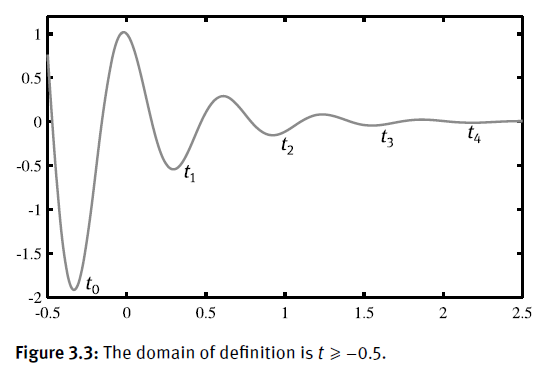
\[y\left(t\right)=e^{-2t} \cos 10t+e^{-3t-6} \sin 2t,0⩽t⩽2\ldotp 5\ldotp\]

  
f = @(t)exp(-2*t).*cos(10*t)+exp(-3*(t+2)).*sin(2*t);
tm = -0.5; tM= 2.5; x=fminbnd(f,tm,tM)

x = 1.5511

関数fminbndで求めた解は、グローバル最適解ではない。

グローバルの最適解を見つけるために、制約区間を分割してそれぞれの区間に最適解を探索し、比較したら、グローバルの最適解が求められる。

  
%著者が作成した関数
function [x,f0] = fminbnd_global(f,xm,xM,n,m,varargin)
% f: 関数
% xm:下限
% xM 上限
% n: 変数の数
% m: 探索の分割数
% varargin: fminbndやfminsearchbndで追加のパラメータ
    f0=Inf; M=ones(n,1);
    if length(xm)==1, xm=xm*M; end
    if length(xM)==1, xM=xM*M; end
    for i=1:m
        if n==1, h=(xM-xm)/m; % univariate problem
            [x1,f1]=fminbnd(f,xm+(i-1)*h,xm+i*h,varargin{:});
        else, x0=xm+(xM-xm).*rand(n,1); % multivariate problem
            [x1,f1,key]=fminsearchbnd(f,x0,xm,xM,varargin{:});
        end % generate random initial points with loops
        if f1<f0, x=x1;
        f0=f1;  end % update the solutions
    end
end %追加した行

例題 3.24:

  
f = @(t)exp(-2*t).*cos(10*t)+exp(-3*(t+2)).*sin(2*t);
tm = -0.5; tM= 2.5; x=fminbnd_global(f,tm,tM,1,10)

x = -0.3340

3.4.2 多変数の決定変数の境界制約による最適化問題(John D’Errico法)

{ $\begin{array}{c} \min_{x\;\textrm{s.t.}x_m \le x\le x_M } f(x) \end{array}$ }

ここで、多変数の関数の制約あり最適化問題に直接関数 fminbnd() と fminsearch()を利用できない。

John D’Errico (fminsearchbnd, fminsearchcon - File Exchange - MATLAB Central)は、決定変数の制約を取り扱うための変換手法を提案した。この方法では、新たな決定変数 $z_i$ を導入し、次のように変換する。

\[x_i =x_{m_i } +\frac{1}{2}(x_{M_i} -x_{m_i } )(\sin z_i +1).\]

${\sin \;z}_i$ は、どんな $z_i$ に対しても [-1, 1] の範囲に収まるため、 $\frac{1}{2}\left(\sin \;z_i +1\right)$ によって [0, 1] の範囲に変換される。
$\left(x_{M_i } -x_{m_i } \right)$ に掛けて最終的に $x_{m_i }$ を加えることで $\left\lbrack x_{m_i } ,x_{M_i } \right\rbrack$ の範囲に収まるようになる。

ただし、 $i$ は多変数 $x$ の要素である。この変換により、制約あり最適化問題を無制約問題に変換でき、多変数にも対応できる。

この方法は、Add-onsでダウンロードした関数 fminsearchbnd で使える。

fminsearchbnd(fun,x0,LB,UB,options,varargin)
fminsearchcon(fun,x0,LB,UB,A,b,nonlcon,options,varargin)

例題 3.25

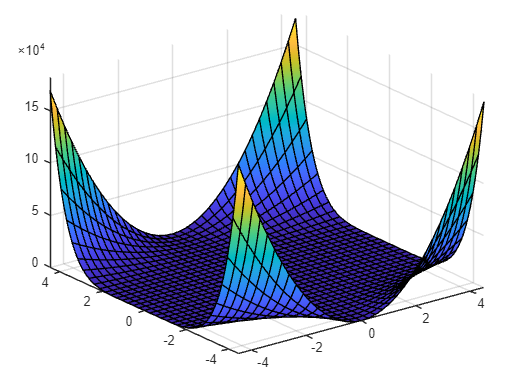
{ $f\left(x_1 ,x_2 \right)={\left(1\ldotp 5-x_1 +x_1 x_2 \right)}^2 +{\left(2\ldotp 25-x_1 +x_1 x_2^2 \right)}^2 +{\left(2\ldotp 625-x_1 +x_1 x_2^3 \right)}^2$ }

  
f=@(x,y) (1.5-x+x*y)^2+(2.25-x+x*y^2)^2 + (2.625-x+x*y^3)^2;
%fsurf(f,[-4.5,4.5])

制約条件： $-4\ldotp 5\le x_1 ,x_2 \le 4\ldotp 5$

  
f0=@(x)f(x(1),x(2));
opt=optimset; opt.TolX=eps; ff.TolFun=eps;
[x1,f1]=fminsearchbnd(f0,[0;0],-4.5*[1;1],4.5*[1;1],opt)

x1 = 2x1    
    3.0000
    0.5000

f1 = 2.6871e-29

opt.TolX=eps; TolX（変数の許容範囲）を eps（機械精度、非常に小さい値）に設定する。
ff.TolFun=eps; 最適化する際の関数値の許容範囲を eps に設定する。

制約条件： $-2\le x_1 ,x_2 \le 2$

  
[x1,f1]=fminsearchbnd(f0,[0;0],-2*[1;1],2*[1;1],opt)

x1 = 2x1    
    2.0000
    0.1701

f1 = 0.5233

グローバル最適解(fminbnd_global)

複数の谷が存在する、もしくは広範囲の探索が必要な問題において、fminsearchbnd() 関数は局所的な最適解に収束してしまい、グローバルな最適解（全体の最適解）を見つけられないことがある。このような問題に対しては、より高度なグローバル最適化手法が必要である。

そのため、fminbnd_global() のようなグローバル最適化ソルバーが推奨されている。fminbnd_global() は、複数の初期点を設定し、ランダムな初期値から最適化を複数回実行することで、局所解ではなくグローバルな最適解を見つける。

例題 3.26

{ $f\left(x_1 ,x_2 \right)={\left(1\ldotp 5-x_1 +x_1 x_2 \right)}^2 +{\left(2\ldotp 25-x_1 +x_1 x_2^2 \right)}^2 +{\left(2\ldotp 625-x_1 +x_1 x_2^3 \right)}^2$ }

制約条件： $-500\le x_1 ,x_2 \le 500$

  
opt=optimset; opt.TolX=eps; ff.TolFun=eps;
[x1,f1]=fminsearchbnd(f0,500*rand(2,1),-500*[1;1],500*[1;1],opt)

 
Exiting: Maximum number of function evaluations has been exceeded
         - increase MaxFunEvals option.
         Current function value: 0.458852 
x1 = 2x1    
 -222.8906
1.0044

f1 = 0.4589

  
[x1,f1]=fminbnd_global(f0,-500,500,2,5,opt)

 
Exiting: Maximum number of function evaluations has been exceeded
         - increase MaxFunEvals option.
         Current function value: 0.455059 

 
Exiting: Maximum number of function evaluations has been exceeded
         - increase MaxFunEvals option.
         Current function value: 0.458036 
x1 = 2x1    
    3.0000
    0.5000

f1 = 1.3945e-24

最適解：[3, 0.5]

まとめ

関数名	境界制約ありの最適化問題の手法	グローバル最適解	多変数	ソース
fminbnd()	黄金探索法と放物線補間	×	×	Matlab
fminsearchbnd()	非線形変換にって制約あり問題を無制約問題に変換する	×	○	Matlabアドイン
fminbnd_global	`制約区間を分割して探索する`	○	○	著者

最適化問題の制約は，境界制約、等式制約、不等式制約がある。この節は、境界制限の最適化手法について解説した。

著者が作成した方法がグローバル最適解が求められるが、最適制御では、最適計算時間が制御サンプル時間より小さくなければならない。

参考資料

Math, Optimization

This post is licensed under CC BY 4.0 by the author.