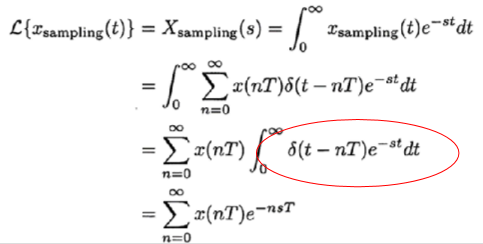Z-transform
定義:
\[X(z)=Z\{x(nT)\}= \sum_{n=0}^{\infty}x(nT)z^{-n}\]4.1 Laplace transform から z 変換
サンプル値のラプラス ⇒ z 変換
- 連続時間信号 $x(t)$ では, Laplace transform を使う
- 離散時間信号 $x(nT)$ では,Z-transform を使う
デルタ関数
Dirac delta function デルタ関数とは,空間の一点にだけ存在する粒子を数式中に表現したいためにディラックによって発明された関数である.理論上の話だが,ある==一点において密度は無限大==,しかしその密度を積分して全体量を求めると有限量であるという性質が欲しかったのである.イメージとしては次のような関数である.インパルス関数とも言われる.
\[\delta(x)= \begin{cases} \infty &(x=0)\\ 0 &(x\neq0) \end{cases}\]例:ハンマーの一撃
- 性質 \(\int_{-\infty}^{\infty} \delta(x) dx = 1\)
他関数に掛け合わされた積分:
\[\int_{-\infty}^{\infty} f(x)\delta(x) dx = f(0)\]サンプリング
離散化,サンプリング,標本化とも呼ばれる.
アナログ信号から時間間隔 $T$ 秒ごとの信号を得る.$T$をサンプリング間隔.1 秒あたりのサンプリング回数($1/T$)をサンプリング周波数.得られた信号はサンプル値信号である.
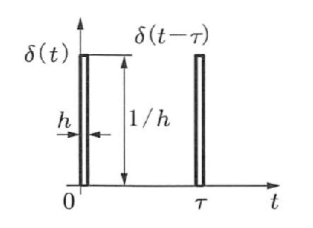
ある時刻の信号を取り出す.
\[\int_{-\infty}^{\infty} f(t)\delta (t-\tau)dt = f(\tau)\] \[\int\_{-\infty}^{\infty} f(t)\delta (t)dt = f(0)\]サンプル値信号( 離散時間信号 ):
\[x_{sample}(t)=\sum_{n=0}^{\infty}x(nT)\delta(t-nT)\]ready/Laplace Transforms すると,
が得られる.
\[z=e^{sT}(=e^{j\omega T})\]ここで,$s=j\omega$.
を代入すると,
\[X_{sample}(s)=X(z)=Z\{x(nT)\}= \sum_{n=0}^{\infty}x(nT)z^{-n}\]これを ==z 変換== という.
z 変換の例:
離散時間インパルス関数 ( $\delta(t)$ ) の z 変換
\[Z\{\delta(n)\}=\delta(0)=1\]離散時間単位ステップ関数( $u(t)$ )の z 変換
\[Z\{u(n)\}=1+z^{-1}+z^{-2}+z^{-3}+\dots=\frac 1{1-z^{-1}}=\frac z{z-1}\]( 等比数列の和による)
等比数列 $x(n)=a^n$ の z 変換
\[Z\{x(n)\}=1+az^{-1}+a^2z^{-2}+a^3z^{-3}+\dots=\frac 1{1-az^{-1}}=\frac z{z-a}\]関数 $x(n)=n$ の z 変換
\[Z\{x(n)\}=0+z^{-1}+2z^{-2}+3z^{-3}+\dots\]漸化式 の求め方により,
- 関数 $x(n)=cos(n\omega T)$ の z 変換
- 関数 $x(n)=sin(n\omega T)$ の z 変換
4.2 Z 変換の性質
ready/Laplace Transforms の s は,微分の意味.( 微分方程式) z 変換 の z は,時間推移の意味.( 差分方程式)
\[Z[x(nT)]=X(z)\](1)Linearity
\[Z[x_1(nT)]=X_1(z), Z[x_2(nT)]=X_2(z)\]のとき,
\[Z[ax_1(nT)+bx_2(nT)]=aX_1(z)+bX_2(z)\](2)推移
a)前移
\[Z[x(nT+mT)]=z^m\{X(z)-\sum_{0}^{m-1} x(nT)z^{-n} \}\]b) ★ 後移
\[Z[x(nT-mT)]=z^{-m}X(z)\]$X(z)$ に $z^{-1}$ が掛け合わされると,信号は 1 サンプル分遅延する.$z^{-1}$ は,遅延演算子である.
(3) 微分 $a^n$ による乗算
\[Z[a^nx(nT)]=X(a^{-1}z)\](4)微分
\[Z[nTx(nT)]=-Tz\frac {dX(z)}{dz}\](5)★ Convolution
\[Y(z)=Z[\sum_{k=0}^{\infty} x(kT)h(nT-kT)]=Z[\sum_{k=0}^{\infty} x(nT-kT)h(kT)]\] \[Y(z)=X(z)H(z)\](6) 初期値定理
\[x(0)=\lim_{x\to\infty} X(z)\](7) 最終値定理
\[\lim_{x\to\infty} x(nT) = \lim_{z\to 1} (1-z^{-1})X(z)\]
4.3 ★ 逆 Z 変換
基本の ready/z-transform:
\[Z[a^n]=1+az^{-1}+a^2z^{-2}+\dots=\frac {1}{1-az^{-1}}=\frac z{z-a}\]==部分分数展開(留数)==
\[X(z)=c_1\frac z{z-a_1}+c_2\frac z{z-a_2}+c_3\frac z{z-a_3}\dots\]によって,
\[x(n)=c_1{a_1^n}+c_2a_2^n+c_3a_3^n\dots (n\geq0)\]が求められる.