Unconstrained MPC
System Modeling
Discrete linear time-invariant system
The dynamics of the system are represented by the following state-space equation:
\[x_{[k+1]}=Ax_{[k]}+Bu_{[k]}\]where:
- $x_{[k]}\in\mathbb{R}^n$ is the states vector at time step $k$.
- $A\in\mathbb{R}^{n\times n}$ is the state transition matrix.
- $u_{[k]}\in\mathbb{R}^{p}$ is the control input vector.
- $B\in\mathbb{R}^{n\times p}$ is the input matrix.
Performance function
\[J_k=\frac{1}{2}x^T_{[h]}Q_fx_{[h]}+\frac{1}{2}\sum^{h-1}_{k=0}\left(x_{[k]}^TQx_{[k]}+u^T_{[k]}Ru_{[k]}\right)\]- $Q_f=\text{diag}(s_1,\dots,s_n)\in\mathbb{R}^{n\times n}, Q_f\ge0$ is the terminal weight matrix.
- $Q=\text{diag}(q_1,\dots,q_n)\in\mathbb{R}^{n\times n}, Q\ge0$ is the state weight matrix.
- $R=\text{diag}(r_1,\dots,r_n)\in\mathbb{R}^{n\times n}, R\ge0$ is the cost weight matrix.
- $h$ is the prediction horizon.
Prediction horizon
In MPC, for time step $k$, the states $x_{[k+1\mid k]},\dots,x_{[k+h\mid k]}$ are predicted.
\[\begin{aligned} x_{[k+1\mid k]} &= Ax_{[k\mid k]}+Bu_{[k\mid k]}\\ x_{[k+2\mid k]} &= Ax_{[k+1\mid k]}+Bu_{[k+1\mid k]}\\ &\quad\vdots \\ x_{[k+h\mid k]} &= Ax_{[k+h\mid k]}+Bu_{[k+h\mid k]} \end{aligned}\]For simple to denote, Define:
\[X_{[k]}:=\begin{bmatrix} x_{[k+1\mid k]}\\ x_{[k+2\mid k]}\\ \vdots \\x_{[k+h\mid k]} \end{bmatrix}\in\mathbb{R}^{nh}\] \[U_{[k]}:=\begin{bmatrix} u_{[k\mid k]}\\u_{[k+1\mid k]}\\\vdots\\u_{[k+h-1\mid k]} \end{bmatrix}\in\mathbb{R}^{ph}\]We have the compact expression for prediction horizon
\[X_{[k]}=A_p x_{[k\mid k]}+B_p U_{[k]}\]where
\[A_p=\begin{bmatrix} A\\ A^2 \\ \vdots \\ A^h \end{bmatrix}\in\mathbb{R}^{nh\times n}\] \[B_p=\begin{bmatrix} B&0_{n\times p}&\dots&0_{n\times p}\\AB&B&\dots&0_{n\times p}\\ \vdots&\vdots &\ddots &\vdots\\ A^{h-1}B&A^{h-2}B&\dots&B \end{bmatrix}\in\mathbb{R}^{nh\times ph}\]Control task
The task is to find the optimal control input sequence:
\[U^\ast_{[k]}:=\begin{bmatrix} u^\ast_{[k\mid k]}\\u^\ast_{[k+1\mid k]}\\\vdots\\u^\ast_{[k+h-1\mid k]} \end{bmatrix}\in\mathbb{R}^{ph}\]which minimizes the performance function $J_k$ .
What we should do is to express the performance function $J_k$ in terms of the control input sequence $U_{[k]}$ so that it forms a standard quadratic programming (QP) problem.
Because solvers for QP problems are well-developed, it is important for MPC to transform the problem into a QP form so that these solvers can effectively solve it.
Solution
Transform the problem into a QP form
\[J_k=\frac{1}{2}x^T_{[k+h\mid k]}Q_fx_{[k+h\mid k]}+\frac{1}{2}\sum^{h-1}_{i=0}\left(x_{[k+i\mid k]}^TQx_{[k+i\mid k]}+u^T_{[k+i\mid k]}Ru_{[k+i\mid k]}\right)\]- Take out the initial cost $x^T_{[k\mid k]}Qx_{[k\mid k]}$ from the sum.
- Rewrite by the compact expression.
- Define the new weight matrix and rewrite.
$x_{[k\mid k]}$ , the initial states for time step $k$, is known.
- According to the prediction horizon, we can express the $X_{[k]}$ in terms of the $U_{[k]}$.
\[X^T_{[k]}Q_pX_{[k]}=x^T_{[k\mid k]}A_p^TQ_pA_p x_{[k\mid k]}+2x^T_{[k\mid k]}A_p^TQ_pB_p U_{[k]}+U_{[k]}^TB_p^TQ_pB_p U_{[k]}\]$x^T_{[k\mid k]}A_p^TQ_pB_p U_{[k]}=U_{[k]}^TB_p^TQ_pA_p x_{[k\mid k]}$
- New performance function
- Obtain the QP form
where
\[F:=B_p^TQ_p^TA_p\in\mathbb{R}^{ph\times n}\] \[H:=R_p+B_p^TQ_pB_p\in\mathbb{R}^{ph\times ph}\] \[C:=\frac{1}{2}x^T_{[k\mid k]}(Q+A_p^TQ_pA_p)x_{[k\mid k]}\]C is a constant regarding initial states.
Analytical solution
\[U_{[k\mid k]}^\ast=-H^{-1}Fx_{[x\mid x]}\] \[u_{[k\mid k]}^\ast=-k_{mpc}x_{[x\mid x]}\]where
\[k_{mpc}:=\begin{bmatrix} I_{p\times p}&0_{p\times p}&\cdots& 0_{p\times p} \end{bmatrix}_{p\times ph}H^{-1}F^T\]Simulation
Function
- transform to QP form
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
%% QP_Transform
%----------------------------------------------------------%
% Youkoutaku: https://youkoutaku.github.io/ %
%----------------------------------------------------------%
% This function is used to transform the cost function of MPc into standard QP form.
function [Ap, Bp, Qp, Rp, F, H] = QP_Transform(A, B, Q, R, Qf,Np)
% Input: A, B, Q, R, Qf, Np
% n is the dimension of states
n = size(A,1);
% p is the dimension of inputs
p = size(B,2);
% Define Ap and Bp for QP
Ap = zeros(Np*n, n);
Bp = zeros(Np*n, Np*p);
% Calculate Ap and Bp for QP
for i = 1:Np
% Ap = [A^1; A^2; ...; A^Np]
Ap(1+(i-1)*n:i*n,:) = A^i;
% Bp = [ B 0_{n×p} 0_{n×p} ... 0_{n×p}
% AB B 0_{n×p} ... 0_{n×p}
% A^2*B A*B B ... 0_{n×p}
% ... ... ... ... ...
% A^(h-1)*B A^(h-2)*B A^(h-3)*B ... B ]
Bp(1+(i-1)*n:i*n, 1:p) = A^(i-1)*B;
for j = 2:Np
Bp(1+(j-1)*n:j*n, 1+(j-1)*p:j*p) = Bp(1+(i-1)*n:i*n, 1+(i-1)*p:i*p);
end
end
% Calculate Qp and Rp for QP
% Qp = diag(Q Q ... Qf)
Qp = kron(eye(Np-1), Q);
Qp = blkdiag(Qp, Qf);
% Rp = diag(R R ... R)
Rp = kron(eye(Np), R);
% F = A' * Qp * Bp
F = Bp'*Qp'*Ap;
% H = Bp' * Qp * Bp + Rp
H = Bp'*Qp*Bp + Rp;
end
- MPC vs LQR
Problem
Consider a simple discrete time system:
\[\begin{bmatrix} \dot x_1 \\ \dot x_2 \end{bmatrix}=\begin{bmatrix} 0 &1\\ 0.5 &0 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}+\begin{bmatrix}0\\ 1 \end{bmatrix}u(t)\]We using the different weight matrix.
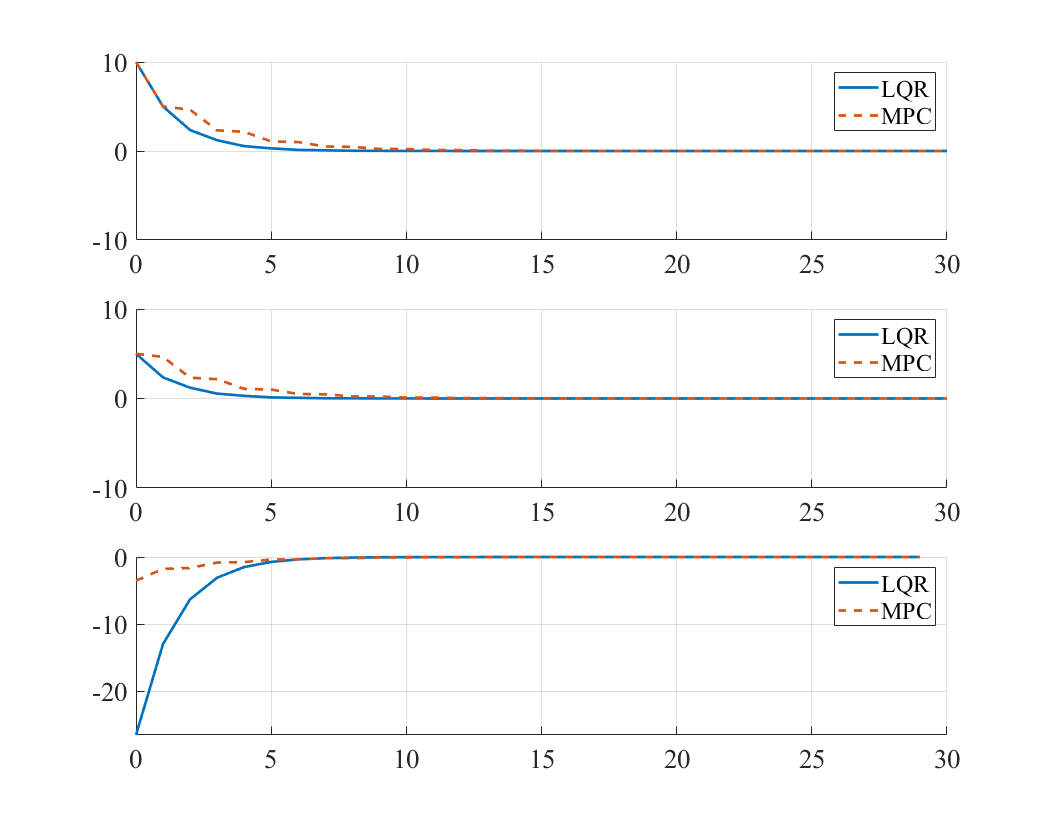
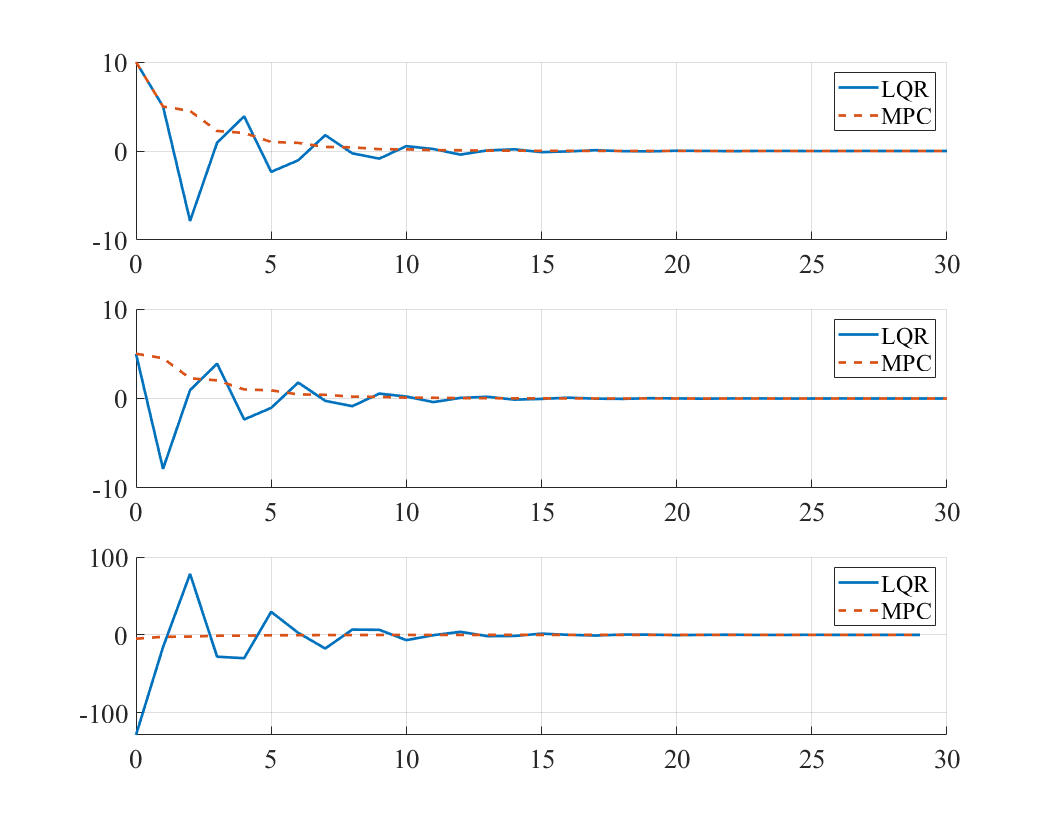
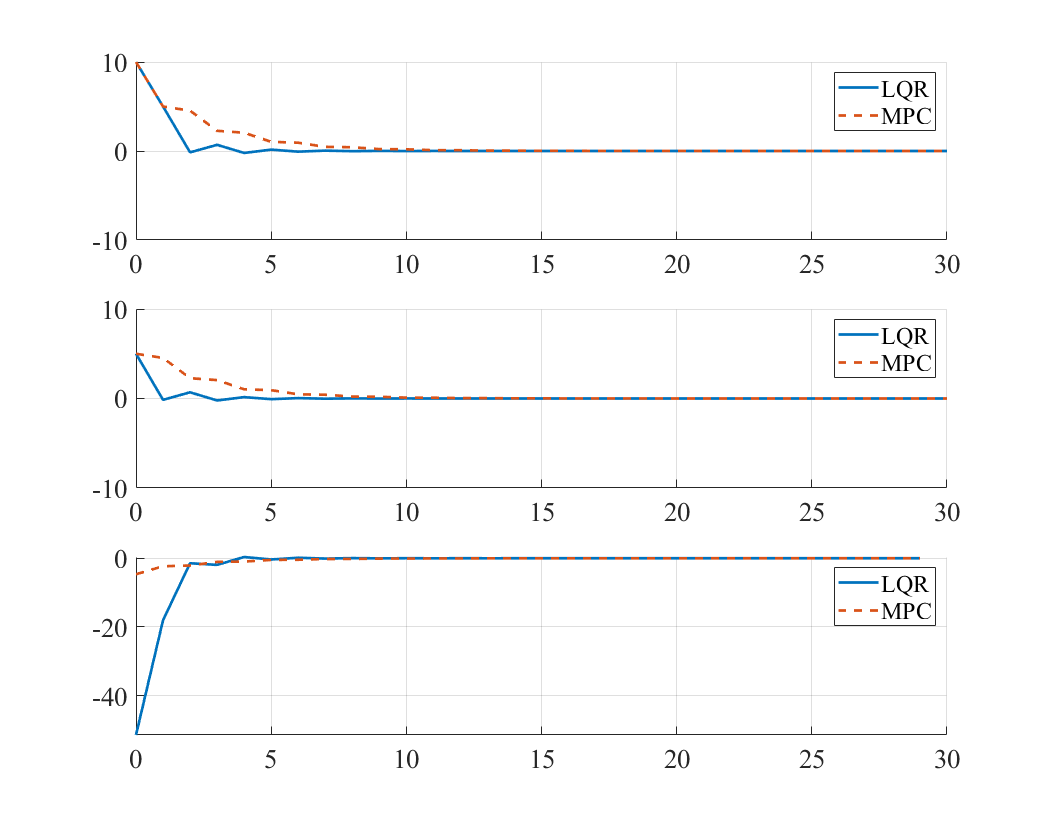
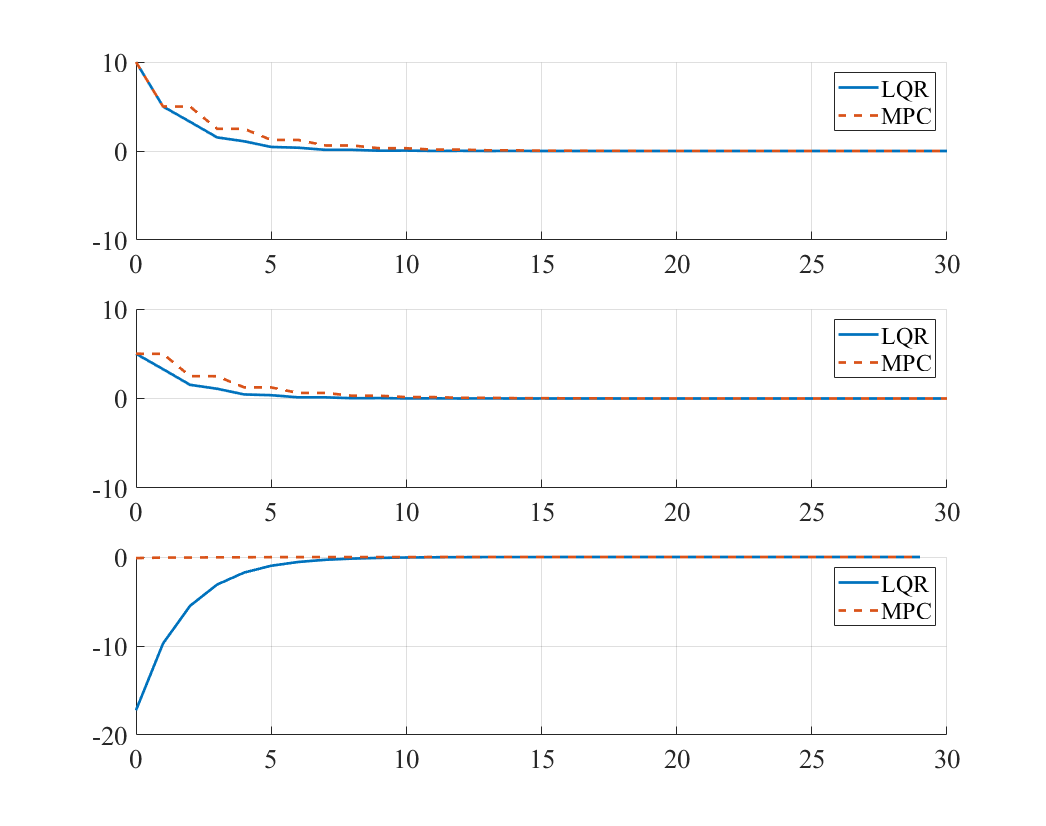
The following figures are showing the $x_1,x_2,u$.
(1)
\[Q=Q_f=\begin{bmatrix} 100 & 0 \\ 0 & 1 \end{bmatrix}, R=1\](2)
\[Q=Q_f=\begin{bmatrix} 10 & 0 \\ 0 & 1 \end{bmatrix}, R=1\](3)
\[Q=Q_f=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, R=1\](4)
\[Q=Q_F=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, R=100\]Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
%% MPC vs LQR
%----------------------------------------------------------%
% Youkoutaku: https://youkoutaku.github.io/ %
%----------------------------------------------------------%
% This script is used to compare the performance of MPC and LQR.
clear;
close all;
clc;
set(0, 'DefaultAxesFontName', 'Times New Roman')
set(0, 'DefaultAxesFontSize', 14)
%% System Model
A = [0 1; 0.5 0];
n= size(A,1);
B = [0; 1];
p = size(B,2);
C = [1, 0];
D = 0;
% the simulation time
Time = 3;
% the sampling time
ts = 0.1;
% the number of the simulation steps
k_steps = Time/ts;
%% Weight matrix
Q = [1 0; 0 1]; % 100, 10, 1
Qf= [1 0; 0 1]; % 100, 10, 1
R = 1; % 1, 100
%% Initialization
% the number of the prediction horizon
Np = 5;
% the state of the system
x0 = [10; 5];
% the state of the system by LQR
x_lqr = x0;
% the state of the system by MPC
x_mpc = x0;
% the history of the state by LQR
xh_lqr = zeros(n,k_steps);
% the history of the state by MPC
xh_mpc = zeros(n,k_steps);
% the history of the input by LQR
uh_lqr = zeros(p,k_steps);
% the history of the input by MPC
uh_mpc = zeros(p,k_steps);
xh_lqr(:,1) = x_lqr;
xh_mpc(:,1) = x_mpc;
%% Riccati equation for LQR
K_lqr = lqr(A,B,Q,R);
%% Transform into QP form for MPC
[Ap, Bp, Qp, Rp, F, H] = QP_Transform(A, B, Q, R, Qf,Np);
%% Simulation - discrete time system
for k = 1 : k_steps
%% MPC
% Calculate the input - MPC
options = optimset('MaxIter', 200);
% Solve the QP problem
[U, fval, exitflag, output, lambda] = quadprog(H, F*x_mpc, [], [], [], [], [], [], [], options);
% u(k) = [I 0 ... 0] * U(k)
u_mpc = U(1:p, 1);
% Calculate the system response - MPC
x_mpc = A * x_mpc + B * u_mpc * ts;
% Save the system state - MPC
xh_mpc(:,k+1) = x_mpc;
% Save the system input - MPC
uh_mpc(:,k) = u_mpc;
%% LQR
% Calculate the input - LQR
u_lqr = -K_lqr * x_lqr;
% Calculate the system response - LQR
x_lqr = A * x_lqr + B * u_lqr * ts;
% Save the system state - LQR
xh_lqr(:,k+1) = x_lqr;
% Save the system input - LQR
uh_lqr(:,k) = u_lqr;
end
%% Plot
% Plot the state x1
figure()
subplot (3, 1, 1);
hold;
plot (0:length(xh_lqr(1,:))-1,xh_lqr(1,:));
plot (0:length(xh_lqr(1,:))-1,xh_mpc(1,:),'--');
grid on
legend("LQR","MPC")
hold off;
%xlim([0 30]);
ylim([-10 10]);
% Plot the state x2
subplot (3, 1, 2);
hold;
plot (0:length(xh_lqr(2,:))-1,xh_lqr(2,:));
plot (0:length(xh_lqr(2,:))-1,xh_mpc(2,:),'--');
grid on
legend("LQR","MPC")
hold off;
%xlim([0 30]);
ylim([-10 10]);
% Plot the input
subplot (3, 1, 3);
hold;
plot (0:length(uh_lqr)-1, uh_lqr(1,:));
plot (0:length(uh_mpc)-1, uh_mpc(1,:),'--');
grid on
legend("LQR","MPC")
hold off;
%xlim([0 30]);
%ylim([-20 20]);
set(findobj('Type','Axes'),'FontSize',20);
set(findobj('Type','Line'),'LineWidth',2);
axesHandles = findobj('Type','Axes');
Reference
- Handbook of Model Predictive Control
- 王天威. 控制之美(卷2). 清华大学出版社. 2023.