Simulation_PID
alt: PID
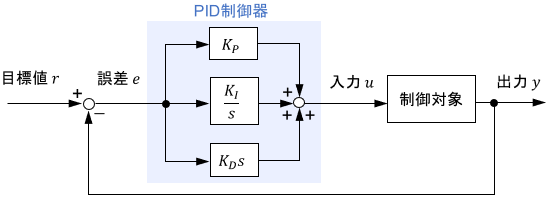
制御対象
\[G(s)=\frac{12s+8}{20s^4+112s^3+147s^2+62s+8}\]状態空間表現に変換する.
1
2
3
4
5
6
7
num = [0 0 12 8];
den = [20 113 147 62 8];
sysg=tf(num, den); %伝達関数
[Ao,Bo,Co,Do] = tf2ss(num,den); %tf2ss伝達関数表現から状態空間表現への変換
PID
$k \to n$ とすると,
\[e(n)=r(n)-y(n-1)\]\[U(z)=E(z)C(z)\]偏差 = 目標値 - 一個前の制御量
z[操作量] = z[偏差]・z[制御器]
PID 制御器伝達関数:
\[C(s)=c_p+c_i\frac{1}{s}+c_d\frac{s}{\gamma s+1}, \quad \gamma=4\times T\]1
2
3
4
gamma=4*T; %γ
cp=6; %比例
ci=1; %積分
cd=7; %微分
前進差分
方法 1
- すごく面倒くさい方法:(諦めよう!) 前進差分による PID 制御器の z 変換:
逆 z 変換(徐々に):
\[u(n)=c_pe(n)+c_i\frac{Te(n-1)}{1-z^{(-1)}}+c_d\frac{e(n)-e(n-1)}{\gamma+(T-\gamma)z^{-1}}\]
- 両辺を $1-z^{-1}$ を掛けると,\(\begin{equation}\begin{aligned}u(n)-u(n-1)=&c_pe(n)-c_pe(n-1)\\ &+c_iTe(n-1)\\ &+\frac{c_d}{\gamma+(T-\gamma)z^{-1}}\left( (e(n)-e(n-1))-(e(n-1)-e(n-2))\right)\end{aligned}\end{equation}\)
- 両辺を $\gamma+(T-\gamma)z^{-1}$ を掛けると,\(\begin{equation}\begin{aligned}\gamma u(n)+(T-\gamma)u(n-1)\\-\gamma u(n-1)-(T-\gamma)u(n-2)=&c_p\gamma \left(e(n)-e(n-1)\right)\\&+(T-\gamma)c_p(e(n-1)-e(n-2))\\&+ c_iT\gamma e(n-1)+c_iT(T-\gamma)e(n-2)\\ &+c_d(e(n)-e(n-1)-e(n-1)+e(n-2))\end{aligned}\end{equation}\)
- 操作量 $u(n)$ \(\begin{equation}\begin{aligned}u(n)=&\frac{1}{\gamma}[c_p\gamma \left(e(n)-e(n-1)\right)\\&+(T-\gamma)c_p(e(n-1)-e(n-2))\\&+ c_iT\gamma e(n-1)+c_iT(T-\gamma)e(n-2)\\&+c_d(e(n)-2e(n-1)+e(n-2)) \\&+(2\gamma-T)u(n-1)+(T-\gamma)u(n-2) ]\\=&( (c_p\gamma + c_d )e(n) \\&+ ( c_p( T- 2\gamma) + c_iT\gamma - 2c_d )e(k-1) \\&+(c_p(\gamma-T)+c_iT(T-\gamma)+c_d )e(k-2) \\&+ (2\gamma-T)u(k-1) + (T-\gamma)u(k-2) ) / \gamma\end{aligned}\end{equation}\)s
1
2
3
u(k)= ( (cp*gamma + cd )*e(k) + ( cp*( T- 2*gamma) + ci*T*gamma - 2*cd )*e(k-1)
+ (cp*(gamma-T)+ci*T*(T-gamma)+cd )*e(k-2)
+ (2*gamma-T)*u(k-1) + (T-gamma)* u(k-2) ) / gamma;
プログラミング化する場合に,e の各項の係数を揃ったら,PC での計算がミスがない.係数が揃えないと,ミスが生じる
方法 2
P-I-Dを分解して,シミュレーションを行うと, P:
\[u_p(n)=c_pe(n)\]偏差を比例したもので制御する
I:
\[u_i(n)=c_i\frac{Tz^{-1}}{1-z^{-1}}e(n)\] \[\begin{equation}u(n)-u_i(n-1)=c_iTe(n-1)\\\to u_i(n)=u(n-1)+c_iTe(n-1)\end{equation}\]偏差の累積で制御する
D:
\[u_d(n)=c_d\frac{1-z^{-1}}{\gamma+(T-\gamma)z^{-1}}e(n)\] \[\begin{equation}\gamma u_d(n)+(T-\gamma)u_d(n-1)=c_d(e(n)-e(n-1)\\\to u_d(n)=\frac{c_d}{\gamma}\left(e(n)-e(n-1)-\frac{T-\gamma}{\gamma}u_d(n-1)\right)\end{equation}\]偏差の変化で制御するつもりだが,初期状態には変化がない. 微分の s× ローパスフィルタ 1/(γs+1)
前進差分による状態空間表現:
\[x(n+1)=x(n)+T(Ax(n)+bu(n))\] \[y(n)=Cx(n)+Du(n)\]状態空間表現において,行列計算を行う.そのためにプログラミングにおける行列の Index を考えなければいけない.
1
x = zeros(4, n+1); %状態変数 4次元
1
2
x(:,k)= x(:,k-1) + T*(Ao*x(:,k-1) + Bo*u(k-1));
y(k)= Co*x(:,k)+Do*u(k);
x(;,k)というように,x の第 k 列のすべて要素で計算を行う
後退差分
後退差分による PID 制御器の z 変換:
\[C(z)=c_p+c_i\frac{T}{1-z^{-1}}+c_d\frac{1-z^{-1}}{T(\frac{\gamma}{T}(1-z^{-1})+1)}=c_p+c_i\frac{T}{1-z^{-1}}+c_d\frac{1-z^{-1}}{\gamma(1-z^{-1})+T}\]PID 分解して,シミュレーションを行うと, P:
\[u_p(n)=c_pe(n)\]I:
\[u_i(n)=c_i\frac{T}{1-z^{-1}}e(n)\] \[\begin{equation}u(n)-u_i(n-1)=c_iTe(n)\\\to u_i(n)=c_iTe(n)+u_i(n-1)\end{equation}\]D:
\[u_d(n)=c_d\frac{1-z^{-1}}{\gamma(1-z^{-1})+T}e(n)\] \[\begin{equation} (\gamma+T)u_d(n)-\gamma u_d(n-1))=c_d(e(n)-e(n-1)) \\\to u_d(n)=\left( c_d(e(n)-e(n-1)) +\gamma u_d(n-1) \right)/(\gamma+T)\end{equation}\]後退差分による状態空間表現:
\[x(n)-x(n-1)=T(Ax(n)+bu(n)) \to x(n)=(I-TA)^{-1}\:(x(n-1)+Tbu(n))\] \[y(n)=Cx(n)+Du(n)\]双 1 次変換法
双一次変換法による PID 制御器の z 変換:
\[\begin{equation} \begin{aligned} C(z)&=c_p+c_i\frac{T}{2}\frac{1+z^{-1}}{1-z^{-1}}+c_d\frac{1}{\gamma+\frac{T(1+z^{-1})}{2(1-z^{-1})}}\\&=c_p+\frac{Tc_i}{2}\frac{1+z^{-1}}{1-z^{-1}}+2c_d\frac{1-z^{-1}}{2\gamma+T+(T-2\gamma)z^{-1}} \end{aligned} \end{equation}\]PID 分解して,シミュレーションを行うと, P:
\[u_p(n)=c_pe(n)\]I:
\[\begin{equation}u_i(n)-u_i(n-1)=\frac{c_iT}{2}(e(n)+e(n-1))\\\to u_i(n)=\frac{c_iT}{2}(e(n)+e(n-1))+u_i(n-1)\end{equation}\]D:
\[\begin{equation}(2\gamma+T)u_d(n)+(T-2\gamma)u_d(n-1)=2c_d(e(n)-e(n-1)) \\\to u_d(n)= \frac{2c_d(e(n)-e(n-1))+(2\gamma-T)u_d(n-1)}{2\gamma+T} \end{equation}\]双一次変換法による状態空間表現:
\[\begin{equation} \begin{aligned} \frac{2}{T}(x(n)-x(n-1))=A(x(n)+x(n-1))+b(u(n)+u(n-1)) \\\to (2I-AT)x(n)=(2I+AT)x(n-1)+bT(u(n)+u(n-1))\\ \to x(n)=(2I-TA)^{-1}[(2I+AT)x(n-1)+bT(u(n)+u(n-1))] \end{aligned} \end{equation}\] \[y(n)=Cx(n)+Du(n)\]行列計算する時,行列の次元注意
1
2
3
4
5
inv() %逆行列
eye() %単位行列I
./
.* %行列個別計算
最も注意すべきなのは,括弧と正負の符号である. 理由は,コードの数式が読みずらい. 解決策:
- コードを LaTex 公式に入れて,確認する.
- 目と手でもう一回計算して確認する
- font 字のサイズ
- x 軸,y 軸 ラベルと単位
- zero-orderHolde により,因果関係である.
1
2
3
4
5
6
7
8
9
10
11
12
13
for k=1:N+1
y(k) = Cx(k) + Du(k)
e(k) = r(k) - y(k)
%離散方法
up(k)=
ui(k)=
ud(k)=
u(k) =
%前進差分で出力
x(k+1)= x(k) + T*( A*x(k)+B*u(K) )
end
- 実際の場合,センサからの観測値をもらうので,y(t)が先の方である.
- しかし,y(t)を先にすると,$y=Cx+Du$ における $u$ がずっと 0 で計算している.普通に $D=0$ ので影響がない.
- また,現在の入力 $u(t)$ を求めたい. $u(t)$ を求めるために,現在の出力(観察値)$y(t)$ が必要である.出力を得るために,現在まだ求めていない入力を使うべきではない.
Simulation
PID
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
clear
close all
set(0,'DefaultAxesFontName','Times New Roman')
set(0,'DefaultAxesFontSize',22)
%--------------------------------------------------------------------
% 同定ゼミ宿題 PID制御器のシミュレーション
% 5/26 by YANG
% 修正済み
%---------------------------------------------------------------------
Tmax = 30; %time
T=0.05; %smap
n=Tmax/T;
gamma=4*T; %gamma
cp=6; %P
ci=1; %I
cd=7; %D
%control object
num = [0 0 12 8];
den = [20 113 147 62 8];
sysg=tf(num, den); %transfer function
[Ao,Bo,Co,Do] = tf2ss(num,den); %switch transfer function to state-space responsentation
%array
t = zeros(1, n+1);
r = ones(1, n+1); %reference
upF = zeros(1, n+1); %p-input
uiF = zeros(1, n+1); %i-input
udF = zeros(1, n+1); %d-input
uF = zeros(1, n+1); %input
xF = zeros(4, n+1); %state v
yF = zeros(1, n+1); %output
eF = zeros(1, n+1); %errer
for k=2:n+1
t(k) = (k-1)*T;
yF(k)= Co*xF(:,k)+Do*uF(k);
eF(k) = r(k)-yF(k);
%Forward difference
upF(k) = cp*eF(k);
uiF(k) = uiF(k-1)+ci*T*eF(k-1);
udF(k) = ( cd*(eF(k)-eF(k-1))-(T-gamma)*udF(k-1) )/gamma;
uF(k) = upF(k) + uiF(k) + udF(k);
xF(:,k+1)= xF(:,k) + T*(Ao*xF(:,k) + Bo*uF(k));
end
%array
upB = zeros(1, n+1); %p-input
uiB = zeros(1, n+1); %i-input
udB = zeros(1, n+1); %d-input
uB = zeros(1, n+1); %input
xB = zeros(4, n+1); %state v
yB = zeros(1, n+1); %output
eB = zeros(1, n+1); %errer
for k=2:n+1
yB(k)= Co*xB(:,k) + Do*uB(k);
eB(k) = r(k) - yB(k);
%Back difference
upB(k) = cp*eB(k);
uiB(k) = ci*T*eB(k) + uiB(k-1);
udB(k) = ( cd*( eB(k) - eB(k-1) ) + gamma * udB(k-1) ) / (gamma+T);
uB(k) = upB(k) + uiB(k) + udB(k);
xB(:,k+1)= xB(:,k) + T*(Ao*xB(:,k) + Bo*uB(k));
end
%array
upD = zeros(1, n+1); %p-input
uiD = zeros(1, n+1); %i-input
udD = zeros(1, n+1); %d-input
uD = zeros(1, n+1); %input
xD = zeros(4, n+1); %state v
yD = zeros(1, n+1); %output
eD = zeros(1, n+1); %errer
for k=2:n+1
yD(k)= Co*xD(:,k)+Do*uD(k);
eD(k) = r(k)-yD(k); %!
%Bilinear transform
upD(k) = cp * eD(k);
uiD(k) = (ci*T)*(eD(k)+eD(k-1))/2 + uiD(k-1) ;
udD(k) = ( 2*cd*(eD(k)-eD(k-1)) + (2*gamma - T)*udD(k-1) ) /(2*gamma+T);
uD(k) = upD(k) + uiD(k) + udD(k);
xD(:,k+1)= xD(:,k) + T*(Ao*xD(:,k) + Bo*uD(k));
end
%subplot(2,1,1); plot(t,uF,t,uB,t,uD); title('u(t)');legend('FD','BD','BT'); ylabel('u(t)'); xlabel('Time[sec]'); grid on
%subplot(2,1,2);
plot(t,yF,t,yB,t,yD,t,r,'--'); title('r(t)&y(t)');legend('FD','BD','BT','r'); ylabel('y(t)'); xlabel('Time[sec]'); grid on
P-I-D 個別比較
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
clear
close all
set(0,'DefaultAxesFontName','Times New Roman')
set(0,'DefaultAxesFontSize',12)
%--------------------------------------------------------------------
% 同定ゼミ宿題 P-I-D個別 制御器のシミュレーション
% 5/26 by YANG
% 修正済み
%---------------------------------------------------------------------
Tmax = 30; %time
T=0.05; %smap
n=Tmax/T;
gamma=4*T; %gamma
cp=6; %P
ci=1; %I
cd=7; %D
%control object
num = [0 0 12 8];
den = [20 113 147 62 8];
sysg=tf(num, den); %transfer function
[Ao,Bo,Co,Do] = tf2ss(num,den); %switch transfer function to state-space responsentation
%array
t = zeros(1, n+1);
r = ones(1, n+1); %reference
up=zeros(1, n+1);
ui=zeros(1, n+1);
ud=zeros(1, n+1);
upF = zeros(1, n+1); %p-input
uiF = zeros(1, n+1); %i-input
udF = zeros(1, n+1); %d-input
uF = zeros(1, n+1); %input
xF = zeros(4, n+1);
xpF = zeros(4, n+1); %state v
xiF = zeros(4, n+1); %state v
xdF = zeros(4, n+1); %state v
yF = zeros(1, n+1);
ypF = zeros(1, n+1); %output
yiF = zeros(1, n+1); %output
ydF = zeros(1, n+1); %output
eF = zeros(1, n+1);
epF = zeros(1, n+1); %errer_p
eiF = zeros(1, n+1); %errer_i
edF = zeros(1, n+1); %errer_d
%Forward difference
for k=2:n+1
t(k) = (k-1)*T;
%P
ypF(k)= Co*xpF(:,k)+Do*up(k);
epF(k) = r(k)-ypF(k);
up(k) = cp*epF(k);
xpF(:,k+1)= xpF(:,k) + T*(Ao*xpF(:,k) + Bo*up(k));
%I
yiF(k)= Co*xiF(:,k)+Do*ui(k);
eiF(k) = r(k)-yiF(k);
ui(k) = ui(k-1)+ci*T*eiF(k-1);
xiF(:,k+1)= xiF(:,k) + T*(Ao*xiF(:,k) + Bo*ui(k));
%D
ydF(k)= Co*xdF(:,k)+Do*ud(k);
edF(k) = r(k)-ydF(k);
ud(k) = ( cd*(edF(k)-edF(k-1))-(T-gamma)*ud(k-1) )/gamma;
xdF(:,k+1)= xdF(:,k) + T*(Ao*xdF(:,k) + Bo*ud(k));
end
%PDI
for k=2:n+1
t(k) = (k-1)*T;
yF(k)= Co*xF(:,k)+Do*uF(k);
eF(k) = r(k)-yF(k);
upF(k) = cp*eF(k);
uiF(k) = uiF(k-1)+ci*T*eF(k-1);
udF(k) = ( cd*(eF(k)-eF(k-1))-(T-gamma)*udF(k-1) )/gamma;
uF(k) = upF(k) + uiF(k) + udF(k);
xF(:,k+1)= xF(:,k) + T*(Ao*xF(:,k) + Bo*uF(k));
end
subplot(2,1,1); plot(t,up,t,ui,t,ud,t,uF); title('u(t)');legend('up','ui','ud','upid'); ylabel('u(t)'); xlabel('Time[sec]'); grid on
subplot(2,1,2); plot(t,ypF,t,yiF,t,ydF,t,yF,t,r,'--'); title('r(t)&y(t)');legend('yp','yi','yd','ypid','r'); ylabel('y(t)'); xlabel('Time[sec]'); grid on
%subplot(3,1,3); plot(t,epF,t,eiF,t,edF,t,eF); title('e(t)');legend('ep','ei','ed','epid');xlabel('t'); grid on
PD
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
clear
close all
set(0,'DefaultAxesFontName','Times New Roman')
set(0,'DefaultAxesFontSize',12)
%--------------------------------------------------------------------
% 同定ゼミ宿題 PD制御器のシミュレーション
% 5/26 by YANG
% 偏差修正済み
%---------------------------------------------------------------------
Tmax = 30; %time
T=0.05; %smap
n=Tmax/T;
gamma=4*T; %gamma
cp=6; %P
ci=1; %I
cd=7; %D
%control object
num = [0 0 12 8];
den = [20 113 147 62 8];
sysg=tf(num, den); %transfer function
[Ao,Bo,Co,Do] = tf2ss(num,den); %switch transfer function to state-space responsentation
%array
t = zeros(1, n+1);
r = ones(1, n+1); %reference
up=zeros(1, n+1);
ui=zeros(1, n+1);
ud=zeros(1, n+1);
upF = zeros(1, n+1); %p-input
uiF = zeros(1, n+1); %i-input
udF = zeros(1, n+1); %d-input
uF = zeros(1, n+1); %input
upd =zeros(1, n+1); %input
xF = zeros(4, n+1);
xpF = zeros(4, n+1); %state v
xiF = zeros(4, n+1); %state v
xdF = zeros(4, n+1); %state v
xpdF=zeros(4, n+1);
yF = zeros(1, n+1);
ypF = zeros(1, n+1); %output
yiF = zeros(1, n+1); %output
ydF = zeros(1, n+1); %output
ypdF = zeros(1, n+1);
eF = zeros(1, n+1);
epF = zeros(1, n+1); %errer_p
eiF = zeros(1, n+1); %errer_i
edF = zeros(1, n+1); %errer_d
epdF = zeros(1, n+1);
%Forward difference
for k=2:n+1
t(k) = (k-1)*T;
ypdF(k)= Co*xpdF(:,k)+Do*upd(k);
epdF(k) = r(k)-ypdF(k);
%PD
up(k) = cp*epdF(k);
ud(k) = ( cd*(epdF(k)-epdF(k-1))-(T-gamma)*ud(k-1) )/gamma;
upd(k) = up(k)+ud(k);
xpdF(:,k+1)= xpdF(:,k) + T*(Ao*xpdF(:,k) + Bo*upd(k)); %x(:,k)
end
for k=2:n+1
t(k) = (k-1)*T;
yF(k)= Co*xF(:,k)+Do*uF(k);
eF(k) = r(k)-yF(k); %!
upF(k) = cp*eF(k);
uiF(k) = uiF(k-1)+ci*T*eF(k-1);
udF(k) = ( cd*(eF(k)-eF(k-1))-(T-gamma)*udF(k-1) )/gamma;
uF(k) = upF(k) + uiF(k) + udF(k);
xF(:,k+1)= xF(:,k) + T*(Ao*xF(:,k) + Bo*uF(k)); %x(:,k)
end
subplot(2,1,1); plot(t,upd,t,uF); title('u(t)');legend('upd','upid'); ylabel('u(t)'); xlabel('t'); grid on
subplot(2,1,2); plot(t,ypdF,t,yF,t,r,'--'); title('r(t)&y(t)');legend('ypd','ypid','r'); ylabel('y(t)'); xlabel('t'); grid on
%subplot(3,1,3); plot(t,epdF,t,eF); title('e(t)');legend('ypd','ypid');xlabel('t'); grid on
This post is licensed under CC BY 4.0 by the author.