Paramater Estimation for Linear Systems
3.1 はじめに
システムの解析,予測,制御,シミュレーション及び異常診断のため,システムの動特性を知る必要がある.システムの入出力信号の観測値に基づいて,ある評価規範のもとで そのシステムをもっともよく記述する数学モデルを決定することを システム同定(System identification)という。このように,統計学に基づいた同定法は大量かつ複雑なデータ処理を必要とする.最小二乗法で代表されるシステムのパラメータ推定手段は実システムに使える.
3.2 最小二乗法の導出 least squares method
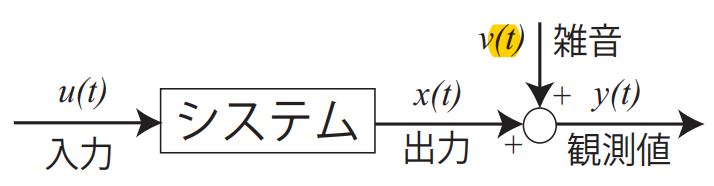
グラフに示すような線形システムの入出力関係を表す数式モデルの記述について考える.線形システムの次数 $n$ を既知と仮定すると,入出力関係は次式のような差分方程式で表される.
\[x_t=-\sum_{i=1}^{n}a_ix_{t-i}+\sum_{i=1}^{n}b_iu_{t-i}\]ただし,$u_t$ と $x_t$ はそれぞれシステムの入出力信号の離散時刻 $t$ におけるサンプル値であ り,$a_i$ と $b_i$ はシステムモデルのパラメータである。 ここで,出力信号 $x_t$には,平均値ゼロの離散値確率雑音 $v_i$ が加わると仮定する.
\[y_t=x_t+v_t\]一般に,観測雑音 $v_t$ はシステムの入力信号 $u_t$ とは,無相関である.すなわち,\(E[u_tv_t]=0\). ただし,$E[・]$ は期待値を意味する.
我々の目的は,システムの入力 $u_t$ と出力の観測値 $y_t$ からシステムのパラメータを推定することである. ここで,$y_t$ の式を差分方程式に代入すると,
\[y_t=-\sum_{i=1}^{n}a_iy_{t-i}+\sum_{i=1}^{n}b_iu_{t-i}+r_t\]が得られる.ただし,観測雑音による誤差は:\(r_t=\sum_{i=0}^{n}a_iv_{t-i}\quad(a_0=1)\) である.ベクトル形式で表現できる.
\[y_t=z_t^T\mathbf{\theta}+r_t\] \[z_t^T=\begin{bmatrix} -y_{t-1},\dots,-y_{t-n},u_{t-1},\dots,u_{t-n} \end{bmatrix}\] \[\mathbf {\theta}=\begin{bmatrix} a_1\\ \vdots \\a_n \\ \vdots \\b_1 \\ \vdots \\ b_n \end{bmatrix}\]システムのパラメータを推定するため,次のような二乗誤差評価を導入する.
\[J=\sum_{t=1}^{N}\rho^{N-t}r_t^2=\sum_{t=1}^{N} \rho^{N-t}(y_t-z_t^T\mathbf{\theta})^2\]ただし,$0<\rho<1$ は忘却係数である.$N$を現在時刻とみれば,$-t$にすると,現在の時間より前の過去の $t$ 個時間の意味である.時間 $t$ が大きいほど,遠くなる過去値が現在に対する影響を意味する.よって,忘却係数が小さくすると,推定値への寄与(貢献)を小さくする役割を果たしており,一種の忘却機能を持っている.この忘却の効果のため,ゆっくり変動する時変パラメータの推定にも適用できる. $J$を 最小にする必要条件 は $\partial J/\partial{\theta}=0$ である.すなわち,
\[\begin{equation} \begin{aligned} \frac{\partial J}{\partial \theta}&= \frac{\partial}{\partial \theta}\left( \sum_{t=1}^{N} \rho^{N-t}(y_t-z_t^T\mathbf{\theta})^2 \right)\\&=-\sum_{t=1}^{N}\rho^{N-t}2z_t(y_t-z_t^T\mathbf{\theta})\\&=-2\sum_{t=1}^{N}\rho^{N-t}z_ty_t+2\sum_{t=1}^{N}\rho^{N-t}z_tz_t^T\theta = 0 \end{aligned} \end{equation}\]ベクトル $A$ とベクトル $x$ の積をベクトル x で微分する. \(\frac{\partial}{\partial x}(Ax)=A^T\) よって,\(\frac{\partial}{\partial \theta}(z_t^T\theta)=z_t\)
より,$\theta$ の最小二乗推定値が得られる($J$が最小にする $\hat\theta$ ).
\[\hat\theta=\left( \sum_{t=1}^{N}\rho^{N-t}z_tz_t^T \right)^{-1}\sum_{t=1}^{N}\rho^{N-t}z_ty_t\]上式が成り立つためには,
\[\left( \sum_{t=1}^{N}\rho^{N-t}z_tz_t^T \right)^{-1}\]が存在しなければならない. 一般に,入力信号 $u(t)$ が十分多くの周波数成分を含んでいればm上記の逆行列が存在する.
$J$ 二乗誤差評価が最小であるときの最小二乗推定値 $\theta$ が分かれば,システムがわかる.( $\theta$ は,システムの差分方程式の係数である.)
3.2.1 推定値の漸近的性質
データが多くなるにつれて,確率極限:
\[plim_{N\to\infty}\hat\theta=\theta\]が成立するとき,$\hat\theta$ は一致推定値であるという. ここで,忘却係数 $\rho=1$,すなわち過去のデータを忘却しない場合について考察する.$\hat\theta$ の式に $y_t=z_t^T\theta+r_t$ を代入すると,
\[\begin{equation} \begin{aligned} plim_{N\to\infty}\hat\theta &=\left( plim_{N\to\infty} \frac{1}{N}\sum_{t=1}^{N}z_tz_t^T \right)^{-1} \left( plim_{N\to\infty} \frac{1}{N} \sum_{t=1}^{N}z_t\{z_t^T\theta+r_t\} \right)\\&=\theta+\left( plim_{N\to\infty} \frac{1}{N} \sum_{t=1}^{N}z_tz_t^T \right)^{-1}\left(plim_{N\to\infty} \frac{1}{N} \sum_{t=1}^{N}z_tr_t\right) \end{aligned} \end{equation}\]が得られる.ベクトル $z_t$ と誤差 $r_t$ は無関係でなければならない,すなわち,
\[plim_{N\to\infty}\frac{1}{N}\sum_{t=1}^{N}z_tr_t=0\]という条件が成り立たなければならない. 一般に上式が成立することが期待できないので,観測雑音のレベルが高い場合,最小二乗推定は一致推定量でなく,偏り(バイアス)を持つ.
3.3 逐次最小二乗法 (Recursive Least Squares)
前に導出した最小二乗法は,データを蓄えておき,データ行列の逆行列を計算して推 定値を得るバッチ処理である。このような方法は繰り返し計算を必要としないことから one-shot 法またはオフライン法とも呼ばれている。しかし,システムの特性を実時間での 監視や,異常の検出と診断には不向きである。 いま,$N$ 個のデータから得られる推定値を $\theta_N$ とする。そこで,$\theta_N$ を過去の推定値及 び時刻 $N$ でのデータより求めることを考える。新しくデータが得られる度に直前の推定値を修正していく方式(逐次計算式) が実現されれば,オンライン推定や実時間推定への適用が可能である。
\[\hat\theta_N=\hat\theta_{N-1}+L_N\varepsilon\]\[\varepsilon_N=y_N-z_N^T\hat\theta_{N-1}\]積分の形である,過去のデータ+比例係数 × 偏差
\[L_N=\frac{P_{N-1}z_N}{\rho_N+z_N^TP_{N-1}z_N}\]式誤差(偏差):観測値-目標値
\[P_N=\frac{1}{\rho_N}\left[P_{N-1}-\frac{P_{N-1}z_Nz_N^TP_{N-1}}{\rho_N+z_N^TP_{N-1}z_N}\right]\]比例係数
ただし,$P_N$ は $2n\times2n$ の行列で,$L_N$ は $2n\times1$ のベクトルである.
(1) 推定値 $\hat\theta_N$ は,1 時刻前の推定値 $\hat\theta_{N-1}$に,式誤差 $y_N-z_N^T\hat\theta_{N-1}$ に比例した修正項を加えることによって生成される.したがって,バッチ処理に比べて記憶容量が少なくすむ。また,逐次計算では逆行列の計算を必要としない。
(2) 上述の逐次アルゴリズムを実行するためには初期値の設定が必要である.通常,次のように選べばよい.
\[\hat\theta_0=O\] \[P_0=\alpha I\]ただし,$\alpha=10^3 \sim 10^5$
(3) 忘却係数 $\rho_N$ も式の推定アルゴリズムの性能を大きく左右する.一般に,忘却係数数が小さいほど,忘却機能が強く働くので,推定速度が速く,パラメータの変動にも 対応できるが,システムに関する情報を速く忘却するので,観測雑音に弱く,推定値が振動的になる。
- 通常,時不変システムのパラメータ推定において,$\rho_N=1$ としても,差し支えないが,忘却係数を時間の経過とともに 1 に近づくように設定したほうが,パラメータの推定値が速く真値へ収束する.
すなわち,最初の内に忘却係数を小さくすうrことによって推定速度を上げるが,推定値ある程度その真値に近づいたら,雑音の影響を軽減するために,忘却係数を 1 とすることによって推定速度を落とす. 2. 一方,時変システムのパラメータ推定において, $\rho_N=0.97\sim0.999$ と,1 よりやや小さい定数にすればよい.忘却係数が小さいほど,時変パラメータへの追従速度が速くなるが,雑音の影響を受けやすくなる.いずれにしても,雑音のレベルが高い場合,時変システムのパラメータ推定は困難である.
3.4 補助変数法によるパラメータ一致推定
ベクトル $z_t$ と同じサイズの補助変数ベクトル $m_t$ を導入し,次のように補助変数法による推定値を得る.
\[\hat\theta_{IV}=\left( \sum_{t=1}^{N}\rho^{N-t}m_tz_t^T \right)^{-1} \sum_{t=1}^{N}\rho^{N-t}m_ty_t\]そこで,忘却係数 $\rho=1$の場合(過去のデータを忘却しない)における補助変数推定値の漸近的性質について考察する.上式の推定値に $y_t=z_t^T\theta+r_t$ を代入して,確率極限をとると,
\[\begin{equation} \begin{aligned} plim_{N\to\infty} &= \left(plim_{N-\infty}\frac{1}{N}\sum_{t=1}^{N} m_tz_t^T \right)^{-1}\left( plim_{N\to\infty} \frac{1}{N}\sum_{t=1}^{N}m_t\{ z_t^T\theta+r_t \} \right) \\&=\theta+\left(plim_{N-\infty}\frac{1}{N}\sum_{t=1}^{N} m_tz_t^T \right)^{-1}\left( plim_{N\to\infty} \frac{1}{N}\sum_{t=1}^{N}m_tr_t\right) \end{aligned} \end{equation}\]が得られる. 以上に,明らかに,補助変数ベクトル $m_t$ が次のような条件を満足すれば,パラメータ推定値は一致推定値である. (1) 逆行列\(\left(plim_{N-\infty}\frac{1}{N}\sum_{t=1}^{N} m_tz_t^T \right)^{-1}\) が存在する. (2) 補助変数ベクトル $m_t$ と式誤差 $r_t$ は無相関である.すなわち,\(plim_{N\to\infty}\frac{1}{N}\sum_{t=1}^{N}m_tr_t=0\) が成り立つ,
補助変数ベクトルの幾つかの構成:
(1) 遅延された入力を利用する:
\[m_t=\left[ u_{t-1-d},\dots,u_{t-n-d},u_{t-1},\dots,t_{t-n} \right]^T\]ただし,$d\ge n$ (2) 遅延された出力を利用する:
\[m_t=[y_{t-1-d},\dots,y_{t-n-d},u_{t-1},\dots,u_{t-n}]^T\]ただし,$d\ge n$ (3) 推定された出力を利用する:
\[m_t=\left[ -\hat x_{t-1},\dots,-\hat x_{t-n},u_{t-1},\dots,u_{t-n} \right]^T\]ただし,推定された出力\(\hat x_t=-\sum_{i=1}^{n}\hat a_i\hat x_{t-i}+\sum_{i=1}^{n}\hat b_iu_{t-i}\) ここで,$\hat a_i,\;\hat b_i$ は何らかの方法で得たパラメータの推定値である(一致推定値でなくてもいい).このように,システムの出力とパラメータを交互に推定することをBootstrap 法(靴のひもかけ) という.
3.4.1 最小二乗法と補助変数法の逐次推定アルゴリズム
最小二乗法と補助変数法に関する逐次推定アルゴリズムをまとめると,以下のようになる.
\[\hat\theta_N=\hat\theta_{N-1}+L_N\varepsilon_N\] \[\varepsilon_N=y_N-\phi_N^T\hat\theta_{N-1}\] \[L_N=\frac{P_{N-1}\psi_N}{\rho_N+\phi_N^TP_{N-1}\psi_N}\] \[P_N=\frac{1}{\rho_N}\left[P_{N-1}-\frac{P_{N-1}\psi_N\phi_N^TP_{N-1}}{\rho_N+\phi_N^TP_{N-1}\psi_N}\right]\]ただし,$P_N$ は $2n\times2n$の行列で,$L_N$ は $2n\times1$ のベクトルである. 上式において, 逐次最小二乗法の場合:
\[\phi_N=z_N,\quad\psi_N=z_N\]逐次補助変数法の場合:
\[\phi_N=z_N,\quad\psi_N=m_N\]Bootstrap 補助変数法に関して,下記の点に留意しておくべきである. 推定された出力を使って補助変数を構成する場合,推定されたシステムの安定性をチェックしなければならない.ここで,補助変数ベクトルは次のように構成されるとする.
\[m_N=\left[ -\hat x_{N-1},\dots,-\hat x_{N-n},u_{N-1},\dots,u_{N-n} \right]^T\]ただし,
\[\hat x_N=-\sum_{i=1}^{n}\bar a_{i,N-1}\hat x_{N-i}+\sum_{i=1}^{n}\hat b_{i,N-1}u_{N-i}\]ここで, $\hat b_{i,N-1}$ は 逐次推定アルゴリズム の式から得られた時刻 $N-1$ における推定値である. $\bar a_{i,N-1}$ は 安定性 を考慮して, 逐次推定アルゴリズム の式から得られた時刻 $N-1$ における推定値 $\hat a_{i,N-1}$ を修正したものである. 時刻 $N$ において,推定出力 $\hat x_N$ を計算するとき,上記システムの極が安定でなければ,値が発散してしまう.したがって,システムの極,すなわち,
\[z^n+\bar a_{1,N-1}z^{n-1}+\dots+\bar a_{n,N-1}=0\]の解が単位円の内部にいれば(複素数の半径が 1 より小さい),システムが安定である. 時刻 $N$ において,推定出力 $\hat x_N$ を計算するとき,$\hat a_{i,N-1}(i=1,2,\dots,n)$で構成されたシステムの極が不安定であった場合,対策として,$\hat a_{i,N-1}(i=1,2,\dots,n)$を安定な領域に戻すことによって修正する.
すなわち,$\hat a_{i,N-1}(i=1,2,\dots,n)$が安定な極を構成していれば,$\bar a_{i,N-1}=\hat a_{i,N-1}(i=1,2,\dots,n)$ とする.そうでなければ,$\hat a_{i,N-1}(i=1,2,\dots,n)$を適当な安定パラメータに置き換える.
複雑な手法として,以下のような「射影」による修正手法もある. 時刻 $N$ において,推定出力 $\hat x_N$ を計算するとき,$\hat a_{i,N-1}(i=1,2,\dots,n)$で構成されたシステムの極が不安定であった場合,対策として,$\hat a_{i,N-1}(i=1,2,\dots,n)$を安定な領域に射影することによって修正する.すなわち,$\hat a_{i,N-1}(i=1,2,\dots,n)$が安定な極を構成していれば,$\bar a_{i,N-1}=\hat a_{i,N-1}(i=1,2,\dots,n)$とする.そうでなければ,$\hat a_{i,N-1}(i=1,2,\dots,n)$を安定な領域へ修正する.アルゴリズムは:
- Step a:
- If $\hat a_{i,N-1}(i=1,2,\dots,n)$ stable then
- $\bar a_{i,N-1}=\hat a_{i,N-1}(i=1,2,\dots,n)$
- Stop
- Else
- $\bar a_{i,N-1}=\bar a_{i,N-2}+0.5*(\hat a_{i,N-1}-\bar a_{i,N-2})$
- Endif
- If $\hat a_{i,N-1}(i=1,2,\dots,n)$ stable then
- Step b:
- If $\bar a_{i,N-1}(i=1,2,\dots,n)$ stable then
- Stop
- Else
- $\bar a_{i,N-1}=\bar a_{i,N-2}+0.5*(\bar a_{i,N-1}-\bar a_{i,N-2})$
- Endif
- If $\bar a_{i,N-1}(i=1,2,\dots,n)$ stable then
- Step c: Go to Step b
上述の修正は,推定出力の計算だけのために行われることに注意されたい。逐次推定アルゴリズムに対しては,推定されたシステムの安定性の如何に関わらず,このような修正をしない。 最初のうち,パラメータ推定値が揺れるので,最初の 50∼100 ステップの推定を最小二乗法で行い,そのあと Bootstrap 補助変数法に切り替えたほうがよい。
3.5 宿題 逐次最小二乗法によるパラメータ推定
3.6 逐次最小二乗法の導出
| [[2023-05-10-Paramater Estimation for Linear Systems#3.2 最小二乗法の導出 least squares method | 最小二乗法]]による二乗誤差評価$\partial J/\partial{\theta}=0$のとき,最小二乗法推定値 $\widehat{\theta}$ )により, |
が得られる.このとき,逆行列を仮定すると,
\[P_N=\left(\sum_{t=1}^N\rho^{N-t}z_t z_t^T\right)^{-1}\]よって,
\[\begin{equation} \begin{aligned} P_N^{-1}&=\left(\sum_{t=1}^N\rho_N^{N-t}z_t z_t^T\right) \\&=\left(\rho_N^{N-1}z_1z_1^T+\rho_N^{N-2}z_2z_2^T+\dots+\rho_{N}z_{N-1}z_{N-1}^T\right)+\rho_{N}^0z_{N}z_{N}^T \\&=\rho_N\sum_{t=1}^{N-1}\rho_N^{N-1-t}z_t z_t^T+z_{N}z_{N}^T \\&=\rho_NP_{N-1}^{-1}+z_Nz_N^T \end{aligned} \end{equation}\]忘却係数 $\rho$ が時不変であれば,$\rho_t=\rho_N$ である. これによって,忘却係数 $\rho$ が小さくなると,昔の事を忘れて $P_N$ が大きくなる.
\[A=\frac{P_{N-1}}{\rho_N},\quad B=1,\quad C^T=\boldsymbol z_N,\quad D=\boldsymbol z_N^T\]逆行列の補題( Woodbury [[伍德伯里矩阵恒等式]]):\((A^{-1}+C^TB^{-1}D)^{-1}=A-AC^T(DAC^T+B)^{-1}DA\)
したがって,
\[\begin{equation} \begin{aligned} P_N&=\frac{1}{\rho_N}P_{N-1}-\frac{1}{\rho_N}P_{N-1}z_N\left[1+z_N^T\frac{P_{N-1}}{\rho_N}z_N\right]^{-1}z_N^TP_{N-1}\frac{1}{\rho_N} \\&=\frac{1}{\rho_N}\left[ P_{N-1} - \frac{P_{N-1}z_Nz_N^TP_{N-1}}{\rho_N+z_N^TP_{N-1}z_N} \right] \end{aligned} \end{equation}\]$P_N$を最小二乗推定値 $\widehat\theta$ に代表すると,
\[\begin{equation} \begin{aligned} \widehat\theta_N&=\left(\sum_{t=1}^N\rho_N^{N-t}z_t z_t^T\right)^{-1}\sum_{t=1}^N\rho_N^{N-t}z_t y_t \\&=P_N\left[\rho_N\sum_{t=1}^{N-1}\rho_N^{N-1-t}z_t y_t+z_{N}y_{N}\right] \end{aligned} \end{equation}\]\[\begin{equation} \begin{aligned} \widehat\theta_N&=P_N\left[ \rho_N P_{N-1}^{-1}\widehat\theta_{N-1}+z_Ny_N \right] \\&=P_N\left[ [P_N^{-1}-z_Nz_N^T]\widehat\theta_{N-1}+z_Ny_N \right]\\&=\widehat\theta_{N-1}+P_Nz_N\left[y_N-z_N^T\widehat\theta_{N-1}\right] \end{aligned} \end{equation}\]この式により,上の式を整理できる.\(\widehat\theta_N=P_N\sum_{t=1}^N\rho^{N-t}z_t y_t\implies P_N^{-1}\widehat\theta_N=\sum_{t=1}^N\rho^{N-t}z_t y_t\)
\[\begin{equation} \begin{aligned} P_Nz_N&=L_N\\&=\frac{1}{\rho_N}\left[ P_{N-1} - \frac{P_{N-1}z_Nz_N^TP_{N-1}}{\rho_N+z_N^TP_{N-1}z_N} \right]z_N\\&=\frac{P_{N-1}z_N}{\rho_N+z_N^TP_{N-1}z_N} \end{aligned} \end{equation}\]$L_N=P_Nz_N$ で $P_N$ が大きくなると,$L_N$ が大きくなる.偏差係数が大きくなるので,偏差に対応する変化が大きいため,前のことを忘れた.
3.7 射影と最小二乗法の幾何学的意味
3.7.1 ベクトル空間と部分分数空間
実数集合 $\mathbb R$ または複素数集合 $\mathbb C$ などは,加減乗除の演算,いわゆる四則演算が定義されている.このような集合を 体 (field) という. 体 $F$ 上のベクトル空間 $X$ は以下のように定義される.
定義 3.7.1
$x,\;y\in X$ および $\alpha\in F$について,$x+y\in X$ と $\alpha x\in X$が定義され,以下の公理(axiom)が満足されるとき, $X$ を 体 $F$ ( $R$ あるいは $C$) 上の線形ベクトル空間という.
線形代数で定義される線形空間の定義.
$F$ 上のベクトル空間 $X$ の 部分空間(subspace) $S$ は $X$ の空ではない部分集合であり, $S$ 自身も同じ $F$ 上のベクトル空間である.
定義 3.7.2 行列の階数と次元
$\mathbb C^m$ 上のベクトルの組 ${ x_1,\dots,x_k }$ は,その 一次結合(線形結合) が 0 であるとき,\(\alpha_1x_1+\dots+\alpha_kx_k=0\)$\alpha_1=\alpha_2=\dots=\alpha_k=0$であれば,一次独立(linearly independent) であるという.逆に,すべては $0$ ではないあるスカラー組 $\alpha_1,\dots,\alpha_k$によって,${ x_1,\dots,x_k }$の一次結合がゼロであれば,${ x_1,\dots,x_k }$は一次従属(linearly dependent) であるという.
$x_i=(a_i,b_i,\dots,n_i)^T$がベクトル,$\alpha_i$がスカラーで \(\alpha_1x_1+\dots+\alpha_kx_k=0\implies [x_1\;\dots\;x_k]\begin{bmatrix}\alpha_1\\\vdots\\\alpha_k\end{bmatrix}=Ax=0\) ベクトル $x_i$ を展開したら,一次結合(線形結合)が行列とベクトルの掛け算はイコール0という型になる.\(\begin{bmatrix} a_1& \dots&a_k \\ \vdots& \ddots&\vdots \\ n_1& \dots &n_k \end{bmatrix}\begin{bmatrix} \alpha_1\\\vdots\\\alpha_k \end{bmatrix}=M_x\alpha=0\) 意味:ベクトル組 ${ x_1,\dots,x_k }$を行列として空間を線形変換すると,零ベクトルになるベクトル $\alpha=(\alpha_1,\dots,\alpha_k)^T$ について検討している.
- この線形変換が成り立つベクトルは,ベクトル $\alpha$ が零ベクトルしかいないと,一次独立(線形独立) である.つまり,ベクトル組 $x$ での行列の階数が次元数と同じであり,線形変換した空間の次元が圧縮されない.
- 逆にこの線形変換が成り立つベクトルは, ベクトル $\alpha$ 以外に存在すると,一次従属(線形連結) である.つまり,ベクトル組 $x$ での行列の階数が次元数より小さく,線形変換した空間の次元が圧縮された.
定義 3.7.3
ベクトル組 ${ x_1,\dots,x_k }\in\mathbb C^n$ の一次結合の全体は,部分空間となり,${ x_1,\dots,x_k }$によって張られる部分空間(subspace spanned by vectors) とよばれる.以下のように表される.\(span\{ x_1,\dots,x_k \}=\left\{ \sum_{i=1}^{n} \beta_i x_i, \;\beta_i\in\mathbb C\right\}\)
${ x_1,\dots,x_n }$が一次独立(線形独立)で,かつ $b\in span{ x_1,\dots,x_n }$ であれば, $b$ は,$x_1,\dots,x_n$ による唯一の一次結合(線形結合)である.
基底ベクトルはお互いに独立であれば,基底ベクトルで張られる空間に存在するベクトルは,当然唯一の座標があるから.
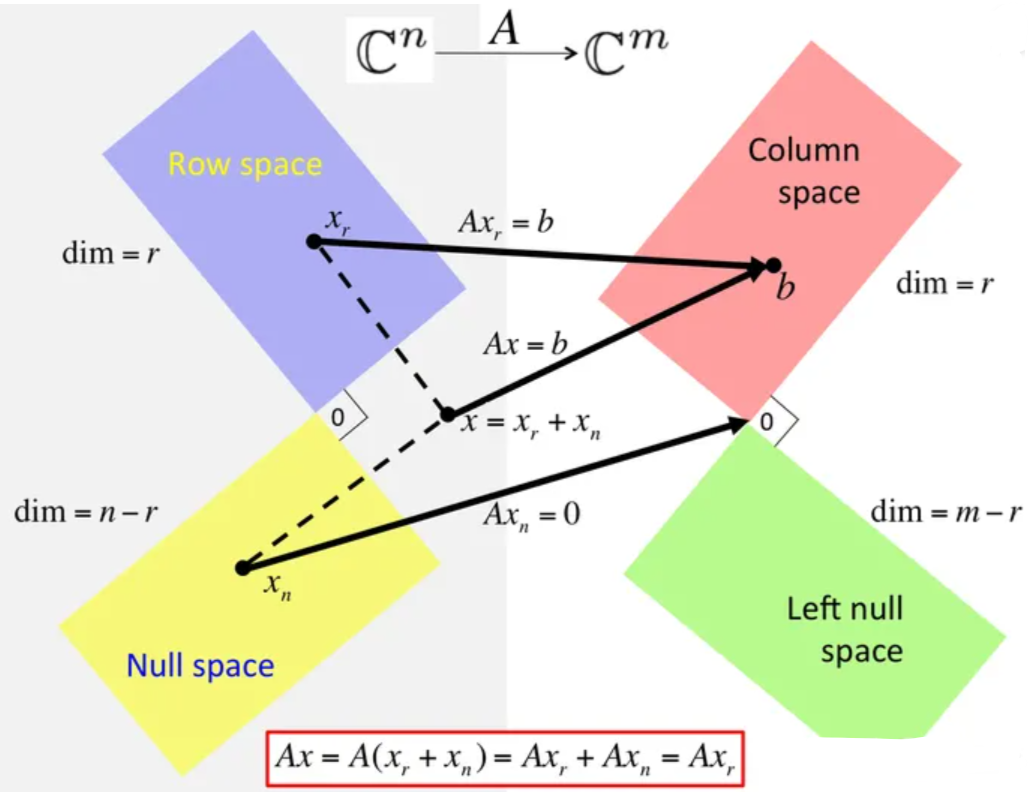
- $X\in\mathbb R^{n\times m}$の列ベクトルによって張られる部分空間 $\mathcal R(X)$ をその列空間という.
3.7.2 行列の階数と次元
列空間と行空間
\[\mathcal R(X) =\{ Xの列ベクトル\{x_1,\dots,x_M\} で張られる部分空間 \}\]\[\mathcal R(X^T)=\{ Xの行ベクトルで張られる部分空間\}\]ベクトル組の線形結合で張られる部分空間は,列空間であること.
行列 $X^T\in\mathbb R^{N\times M}$について,階数 $r$ は,独立な列の最大個数あるいは独立な行の最大個数である.
\[dim\mathcal R(X)=dim\mathcal R(X^T)=r\]行空間と左零空間
\[\alpha^T(x_1,\dots,x_k)=x^TA=0\]左零空間:
\[\mathcal N(X^T)=\{n\in\mathbb R^N| X^Tn=0\}\] \[dimN(X^T)=N-r\]列空間と左零空間が直交している.
\[\mathcal R(X)\;\bot\;\mathcal N(X^T),\;\mathcal (R(X))^{\bot}=\mathcal N(X^T),\;\mathcal (N(X^T))^{\bot}=\mathcal R(X)\]列空間と左零空間の和空間は,空間全体である.
\[\mathcal R(X)\oplus \mathcal N(X^T)=\mathbb R^N\]行空間と零空間
核空間
\[\mathcal N(X)=\{h\in\mathbb R^M| Xh=0\}\] \[dimN(X)=M-r\] \[\mathcal R(X^T)\;\bot\;\mathcal N(X),\;\mathcal (R(X)^T)^{\bot}=\mathcal N(X),\;\mathcal (N(X))^{\bot}=\mathcal R(X^T)\] \[\mathcal R(X^T)\oplus \mathcal N(X)=\mathbb R^M\]3.7.3 射影と最小二乗法
直線への射影=ベクトルの内積
\[y^Tx=x^Ty=||x||\cdot||y||\cos\theta\]射影
$y$ が $x$ への射影 $y_r=ax$ とおくと,( $a$ がスカラー,単なる比例を表す)
\[(y-y_r)^Tx=(y-ax)^Tx=0,\quad a=\frac{y^Tx}{x^Tx}=\frac{x^Ty}{x^Tx}\]\[\boldsymbol{y}_r=h\boldsymbol{x}=\frac{\boldsymbol{x}^T\boldsymbol{y}}{\boldsymbol{x}^T\boldsymbol{x}}\boldsymbol{x}=\bigg[(\boldsymbol{x}^T\boldsymbol{x})^{-1}\boldsymbol{x}\boldsymbol{x}^T\bigg]\boldsymbol{y}=\bigg[\boldsymbol{x}(\boldsymbol{x}^T\boldsymbol{x})^{-1}\boldsymbol{x}^T\bigg]\boldsymbol{y}\]つまり,ベクトルがベクトルの線形結合である.元の $y$ ベクトルを $x$ ベクトルへの方向の成分を除くと,垂直成分しかないので,内積(射影)はゼロである.
射影と最小二乗法
モデル:
\[\begin{aligned} &\textbf{y}=\textbf{y}_r+\textbf{y}_n \\ &{\boldsymbol{y}}_{r}= Xh \\ &{X}{=} [\boldsymbol{x}_1,\cdots,\boldsymbol{x}_M]\in R^{N\times M} \\ &h= [h_1,\cdots,h_M]^T \end{aligned}\]$X$の列空間$\mathcal R(X)$上の任意のベクトル $Xg$ について考えると,$y_n$ が $Xg$ に垂直すれば,
\[\begin{aligned} (\boldsymbol{X}\boldsymbol{g})^{T}\boldsymbol{y}_{n}& =(\boldsymbol{X}\boldsymbol{g})^T(\boldsymbol{y}-\boldsymbol{y}_r) \\ &=\pmb{g}^T\pmb{X}^T(\pmb{y}-\pmb{X}\pmb{h}) \\ &=\boldsymbol{g}^T(\boldsymbol{X}^T\boldsymbol{y}-\boldsymbol{X}^T\boldsymbol{X}\boldsymbol{h})=0 \end{aligned}\]よって,すべての $g$ について成り立つために,
\[X^Ty=X^TXh=X^Ty_r\]つまり,部分空間 X に存在する任意のベクトル g に対して,あるベクトル y のベクトル成分 $y_n$ と垂直すれば,y が部分空間 X への射影は $y_r$ である.
すなわち,
3.8 一般化逆行列と最小二乗法
正則な正方行列の逆行列 $A^{−1}$ は唯一に存在し,かつ $AA^{−1} = A^{−1}A = I$ が成り立つ. 正則な正方行列の逆行列を長方行列或いは特異な正方行列の場合に拡張したものが 一般化逆行列 (generalized inverse) である.一般化逆行列を用いれば,最小二乗法に対して統 一した理論的解釈が可能である
3.8.1 ムーア・ペンローズの逆行列
$A$の任意の $m\times n$行列とする.以下の四つの条件を満足する行列 $G$ を ムーア・ペンローズ(Moore-Penrose) の一般化逆行列という.
\[\begin{equation}\begin{aligned} (1)&& AGA&=A\\ (2)&& (AG)^H&=AG\\ (3)&& GAG &= G\\ (4)&& (GA)^H&=GA \end{aligned} \end{equation}\]この一般化逆行列は, 擬似逆行列(pseudo inverse) またはムーア・ペンローズの逆行列(Moore-Penrose inverse)ともいい,$A^+$ で表す. より一般に,行列 $G$ が上記の四つのうちの一部 $(i),(j),(k), i, j, k = 1, 2, 3, 4$ だけを満足する場合,$G$ を行列 $A$ の ${i, j, k}$ 逆行列 $({i, j, k} inverse)$ という.たとえば,行列 $G$ が条件 (1),(2),(3) を満足し,条件 (4) を満足しない場合,$G$ を行列 $A$ の ${1, 2, 3}$ 逆行列 という. 以下に工学の分野で最もよく応用されている二つのムーア・ペンローズの逆行列につい て紹介する.