Laplace transform
3.1 フーリエ変換からラプラス変換へ
Fourier transform と ラプラス変換 が存在する条件
\[\int_{-\infty}^{\infty} |f(t)|dt < \infty\]- 独立波 : 絶対可積分,フーリエ変換できる.
持続波 : 絶対可積分ではなく,フーリエ変換でない!フーリエ変換存在しない!積分が発散する!
- フーリエ変換は,絶対可積分とは限らない.いつも応答があるわけではない,発散する可能性がある
- ラプラス変換は,絶対可積分 $s=\sigma+j\omega$ で$e^{-\sigma}$があるので,収束できるようになる.
$f(t)e^{-at},a>0$をすると,信号が収束する.絶対可積分になる.
\[F(\omega)=\int_{-\infty}^{\infty} [f(t)e^{-at}]e^{-j\omega t}dt\] \[a+j\omega → s\]また,因果律により, $x(t),t\ge0$について考えるべきである. すなわち,
\(X(\omega)=\int_{0}^{\infty} x(t)e^{-j\omega t}dt\) が発散ならば,収束できるように変換する.
\[\int*{0}^{\infty} [x(t)e^{-at}] e^{-j\omega t}dt = \int*{0}^{\infty} x(t)e^{-(a+j\omega) t}dt\]Laplace Transforms
\[X(s)=\int_{0}^{\infty} x(t)e^{-st}dt\]
畳み込み定理
\[F(f*g)=F(f)・F(g)\]ただし $F(f)$は関数 $f$ の Fourier transform である。この定理は Laplace Transforms・z-transform やメリン変換といった変換に対しても適用できる。
フーリエ変換を使って畳み込み演算を単純な掛け算に変換することが出来る。離散系での関数の場合、定義通りの畳み込み計算をしないで、関数 $f,g$ の 高速フーリエ変換 (FFT) を掛け算した結果を逆高速フーリエ変換 (IFFT) をすることで、高速に畳み込みの計算処理をするのが一般的である。
3.2 逆ラプラス変換
部分分数展開(ヘビサイドの公式)によって,ラプラス変換表を使うのが多い.実際に計算するのがめったにない.
\[x(t)=\frac {1}{2\pi j}\int_{a-j\infty}^{a-j\infty} X(s)e^{st}ds\]3.3 ラプラス変換の性質
- 時間軸の移動
- 減衰性
- 相似性
- 微分
- 初期値定理
- 最終値定理
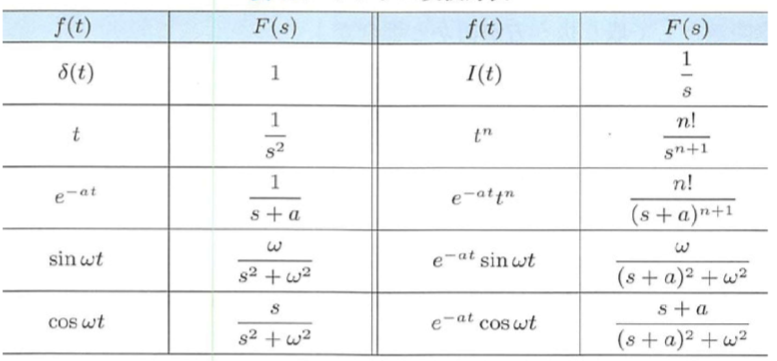
3.4 ラプラス変換表
This post is licensed under CC BY 4.0 by the author.