LQR simulation

Problem

Consider a simple system:

\[\begin{bmatrix} \dot x_1 \\ \dot x_2 \end{bmatrix}=\begin{bmatrix} 0 &1\\ 0.5 &0 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}+\begin{bmatrix}0\\ 1 \end{bmatrix}u(t)\]

We using the algebraic Riccati equation for LQR in the different weight matrix.

(1)

\[Q_1=\begin{bmatrix} 100 & 0 \\ 0 & 1 \end{bmatrix}, R_1=1\]

(2)

\[Q_2=\begin{bmatrix} 1 & 0 \\ 0 & 100 \end{bmatrix}, R_2=1\]

(3)

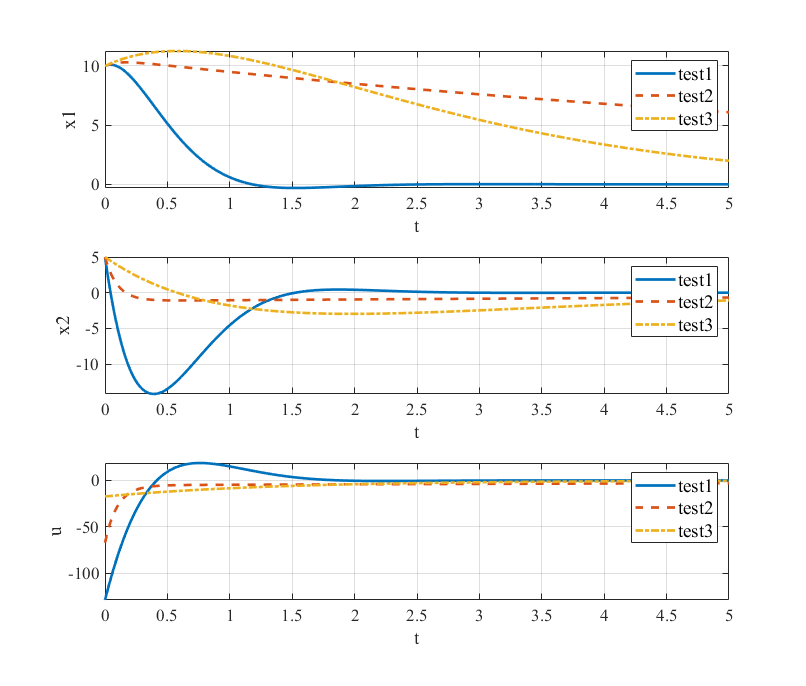
\[Q_1=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, R_3=100\]

---

(1) In the weight matrix, the $x_1$ is most important. Therefore, it is most fast to cover for $x_1$.

(2) In the weight matrix, the $x_2$ is most important. Therefore, it is most fast to cover for $x_2$.

(3) In the weight matrix, the $u$ is most important. Therefore, it is the minimum cost (input).

Simulation

%-----------------------------------------------------------------------%
%                            LQR for simple test                        %
%                                                          Youkoutaku   %
%                                         https://youkoutaku.github.io/ %
%-----------------------------------------------------------------------%
clear;
close all;
clc;
set(0, 'DefaultAxesFontName', 'Times New Roman')
set(0, 'DefaultAxesFontSize', 14)
%========================================%
%           System Model
%========================================%
A = [0 1; 0.5 0];
n= size (A,1);
B = [0; 1];
p = size(B,2);
C = [1, 0];
D = 0;

%========================================%
%           Weight matrix
%========================================%
q1 = [100 0;0 1];
q2 = [1 0;0 100];
q3 = [1 0;0 1];
r1 = 1;
r2 = 1;
r3 = 100;

%========================================%
%           Initial value
%========================================%
x0 = [10;5]; 
x = x0;

%========================================%
%           Riccati equation
%========================================%
[P1,L1,G1] = care(A,B,q1,r1);
K1=inv(r1)*B'*P1;

[P2,L2,G2] = care(A,B,q2,r2);
K2=inv(r2)*B'*P2;

[P3,L3,G3] = care(A,B,q3,r3);
K3=inv(r3)*B'*P3;

%========================================%
%           System 
%========================================%
sys_1=ss(A-B*K1,[0;0],C,D);
sys_2=ss(A-B*K2,[0;0],C,D);
sys_3=ss(A-B*K3,[0;0],C,D);

%========================================%
%           Simulation
%========================================%
ts = 0.01;
t=0:ts:5;
[y1,t,x1]=initial(sys_1,x,t);
[y2,t,x2]=initial(sys_2,x,t);
[y3,t,x3]=initial(sys_3,x,t);

%========================================%
%           Plot
%========================================%
figure();
subplot(3,1,1);
plot(t,x1(:,1),"linewidth",2);
hold on;
plot(t,x2(:,1),'--',"linewidth",2);
hold on;
plot(t,x3(:,1),'-.',"linewidth",2);
legend('test1','test2','test3',"FontSize",14);
xlim([0 5]);
xlabel("t")
ylabel("x1")
grid on;
hold off;

subplot(3,1,2);
plot(t,x1(:,2),"linewidth",2);
hold on;
plot(t,x2(:,2),'--',"linewidth",2);
hold on;
plot(t,x3(:,2),'-.',"linewidth",2);
legend('test1','test2','test3',"FontSize",14);
xlim([0 5]);
xlabel("t")
ylabel("x2")
grid on;
hold off;

subplot(3,1,3);
plot(t,-K1*x1',"linewidth",2);
hold on;
plot(t,-K2*x2','--',"linewidth",2);
hold on;
plot(t,-K3*x3','-.',"linewidth",2);
legend('test1','test2','test3',"FontSize",14);
xlim([0 5]);
xlabel("t")
ylabel("u")
grid on;
hold off;