Post

LQR for set-point regulation

Posted
By Guang-Ze Yang 3 min read

Problem Formulation

Consider a discrete-time linear system, the state-space equation is as

\[x_{[k+1]}=f(x_{[k]},u_{[k]})=Ax_{[k]}+Bu_{[k]}\]

where $x_{[k]}\in\mathbb{R}^n,u_{[k]}\in\mathbb{R}^p$ are system state and input, $A_{[k]}\in\mathbb{R}^{n\times n}$, $B_{[k]}\in\mathbb{R}^{n\times p}$ are state matrices for system.

The constant reference is as

\(x^r_{[k+1]}=A_rx^r_{[k]}\)

  • $A_r=I$

Define the augmented states as

\[\begin{bmatrix} x_{[k+1]}\\x^r_{[k+1]} \end{bmatrix}=\begin{bmatrix} A &0_{n\times n}\\0_{n\times n} &A_r \end{bmatrix}\begin{bmatrix} x_{[k]}\\x^r_{[k]} \end{bmatrix}+\begin{bmatrix} B\\0 \end{bmatrix}u_{[k]}\]

where

\[z_{[k]}:=\begin{bmatrix} x_{[k]}\\x^r_{[k]} \end{bmatrix}, A_z:=\begin{bmatrix} A &0_{n\times n}\\0_{n\times n} &A_r \end{bmatrix}, B_z:=\begin{bmatrix} B\\0 \end{bmatrix}\]

Then, we have

\[z_{[k+1]}=A_zz_{[k]}+B_zu_{[k]}\]

Define the tracking error as

\[e_{[k]}=x_{[k]}-x^r_{[k]}\] \[e_{[k]}=[I_{n\times n}\;-I_{n\times n}]z_{[k]}=C_zz_{[k]}\]

Define the quadratic performance function as

\[J=h\left(e_{[N]}\right)+\sum_{k=0}^{N-1}g\left(e_{[k]},u_{[k]}\right)\]

where

\[\begin{aligned}&h\left(e_{[N]}\right)=\frac{1}{2}e_{[N]}^TSe_{[N]}\\&g\left(e_{[k]},u_{[k]}\right)=\frac{1}{2}[e_{[k]}^TQ_{[k]}e_{[k]}+u_{[k]}^TR_{[k]}u_{[k]}]\end{aligned}\]

Solving

\[J= \frac{1}{2}e_{[N]}^TSe_{[N]} +\frac{1}{2}\sum_{k=0}^{N-1}[e_{[k]}^TQ_{[k]}e_{[k]}+u_{[k]}^TR_{[k]}u_{[k]}]\] \[J= \frac{1}{2}(C_zz_{[N]}) ^TS(C_zz_{[N]}) +\frac{1}{2}\sum_{k=0}^{N-1}[(C_zz_{[k]})^TQ_{[k]}C_zz_{[k]}+u_{[k]}^TR_{[k]}u_{[k]}]\] \[J= \frac{1}{2}z_{[N]}^{T}(C_z^TSC_z)z_{[N]} +\frac{1}{2}\sum_{k=0}^{N-1}[z_{[k]}^T(C_z^TQ_{[k]}C_z)z_{[k]}+u_{[k]}^TR_{[k]}u_{[k]}]\]
  • $S^z=C_z^TSC_z$
  • $Q^z=C_z^TQC_z$
\[J= \frac{1}{2}z_{[N]}^{T}(S^z)z_{[N]} +\frac{1}{2}\sum_{k=0}^{N-1}[z_{[k]}^TQ^z_{[k]}z_{[k]}+u_{[k]}^TR_{[k]}u_{[k]}]\]

According to LQR Gain ($x \to z$), the optimal control input:

\[u^*_{[N-k]}=-F_{[N-k]}z_{[N-k]}\]

where

\[F_{[N-k]}=(B^{T}P_{[k-1]}B+R)^{-1}B^{T}P_{[k-1]}A\]

Notice that the optimal control input is to regular the error $e$, not the augmented states $z$.

The optimal cost to go:

\[J_{N-k\to N}^{*}(z_{[N-k]})=\frac{1}{2}z_{[N-k]}^TP_{[k]}z_{[N-k]}\]

where

\[P_{[k]}=(A-BF_{[N-k]})^TP_{[k-1]}(A-BF_{[N-k]})+F_{[N-k]}^TRF_{[N-k]}+Q\] \[P_{[0]}=S^z\implies P_{[1]}, u^*_{[N-1]}\implies \cdots P_{[k]}, u^*_{[N-k]} \cdots \implies P_{[N]}, u^*_{[0]}\]

Test

Problem

Consider a simple system:

\[\begin{bmatrix} \dot x_1 \\ \dot x_2 \end{bmatrix}=\begin{bmatrix} 0 &1\\ 0 &0 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}+\begin{bmatrix}0\\ 1 \end{bmatrix}u(t)\] \[x^r(t)=\begin{bmatrix} 10\\ 0\\ \end{bmatrix}\]
  • weight matrix
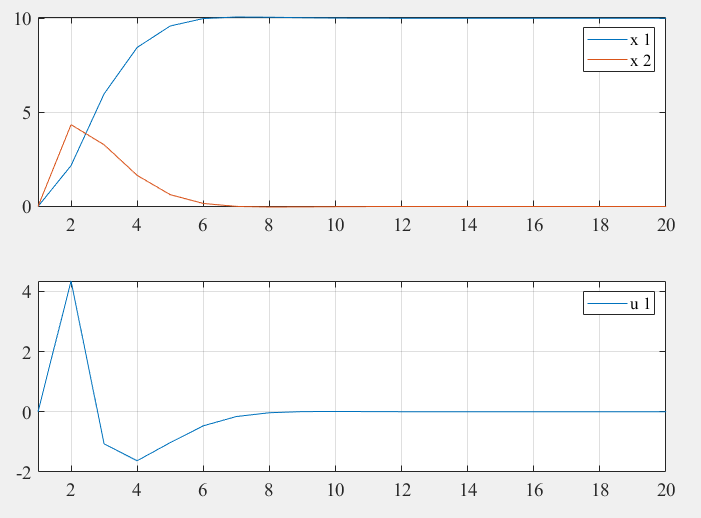
\[Q=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, S=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, R=0.1\]

Simulation

Using the function F1_LQR.m.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90

%% LQR for Tracking
%-----------------------------------------------%
% Youkoutaku:  https://youkoutaku.github.io/    %
%-----------------------------------------------%
% F1_LQR.m is a function to solve the LQR problem by dynamic programming.
% F = F1_LQR(A,B,Q,R,S) solves the LQR problem.

clear;
close all;
clc;
set(0, 'DefaultAxesFontName', 'Times New Roman')
set(0, 'DefaultAxesFontSize', 14)

%% System Model
A = [0 1; 0 0];
n = size(A, 1);
B = [0; 1];
p = size(B, 2);

C = [1 0; 0 1];
D = [0; 0];
%% System Setting
Ts = 1; %Sample time
sys_d = c2d(ss(A, B, C, D), Ts); %discretization of continuous time system
A = sys_d.a; %discretized system matrix A
B = sys_d.b; %discretized input matrix B

%% Weight matrix
Q = [1 0; 0 1]; %R^(n x n) tracking error weight

S = [1 0; 0 1]; %R^(n x n) reference weight

R = 1; %R^(p x p) input weight

%% Initial state
x0 = [0; 0];
x = x0;

%input init
u0 = 0;
u = u0;

%% Reference Signal
xr = [10; 0];

Ar = eye(n); % Augmented matrix

z = [x; xr];

%% LQR Gain
Cz = [eye(n) -eye(n)];
Az = [A zeros(n); zeros(n) Ar];
Bz = [B; zeros(n, 1)];
Sz = Cz.' * S * Cz;
Qz = Cz.' * Q * Cz;

[F] = F1_LQR(Az, Bz, Qz, R, Sz);

%% Simulation
k_steps = 20;
x_h = zeros(n, k_steps);
x_h(:, 1) = x;
u_h = zeros(p, k_steps);
u_h(:, 1) = u;

for k = 1:k_steps
    u =- F * z;
    %System
    x = A * x + B * u;
    z = [x; xr];
    x_h(:, k + 1) = x;
    u_h(:, k + 1) = u;
end
%% Figure
subplot(2, 1, 1);
for i = 1:n
    plot(x_h(i, :));
    hold;
end
legend(num2str((1:n)', 'x %d'));
xlim([1, k_steps]);
grid on
subplot(2, 1, 2);
for i = 1:p
    plot(u_h(i, :));
    hold;
end
legend(num2str((1:p)', 'u %d'));
xlim([1, k_steps]);
grid on

1
2
3

>> F
F =   
	0.4345    1.0284   -0.4345    0.0040

Reference

Control Theory, Model Predict Control
Optimal Control LQR
This post is licensed under CC BY 4.0 by the author.