Post

LQR for regulators

Posted
By Guang-Ze Yang 5 min read

Problem Formulation

Consider a discrete-time linear system, the state-space equation is as

\[x_{[k+1]}=f(x_{[k]},u_{[k]})=Ax_{[k]}+Bu_{[k]}\]

where $x_{[k]}\in\mathbb{R}^n,u_{[k]}\in\mathbb{R}^p$ are system state and input, $A_{[k]}\in\mathbb{R}^{n\times n}$, $B_{[k]}\in\mathbb{R}^{n\times p}$ are state matrices for system.

The constant reference is as

\[x^r_{[k+1]}=A_rx^r_{[k]}\]
  • $A_r=I$

Define the augmented states as

\[\begin{bmatrix} x_{[k+1]}\\x^r_{[k+1]} \end{bmatrix}=\begin{bmatrix} A &0_{n\times n}\\0_{n\times n} &A_r \end{bmatrix}\begin{bmatrix} x_{[k]}\\x^r_{[k]} \end{bmatrix}+\begin{bmatrix} B\\0 \end{bmatrix}u_{[k]}\]

where

\[z_{[k]}:=\begin{bmatrix} x_{[k]}\\x^r_{[k]} \end{bmatrix}, A_z:=\begin{bmatrix} A &0_{n\times n}\\0_{n\times n} &A_r \end{bmatrix}, B_z:=\begin{bmatrix} B\\0 \end{bmatrix}\]

Then, we have

\[z_{[k+1]}=A_zz_{[k]}+B_zu_{[k]}\]

Define the tracking error as

\[e_{[k]}=x_{[k]}-x^r_{[k]}\] \[e_{[k]}=[I_{n\times n}\;-I_{n\times n}]z_{[k]}=C_zz_{[k]}\]

Define the quadratic performance function as

\[J=h\left(e_{[N]}\right)+\sum_{k=0}^{N-1}g\left(e_{[k]},u_{[k]}\right)\]

where

\[\begin{aligned}&h\left(e_{[N]}\right)=\frac{1}{2}e_{[N]}^TSe_{[N]}\\&g\left(e_{[k]},u_{[k]}\right)=\frac{1}{2}[e_{[k]}^TQ_{[k]}e_{[k]}+u_{[k]}^TR_{[k]}u_{[k]}]\end{aligned}\]

Solving

\[J= \frac{1}{2}e_{[N]}^TSe_{[N]} +\frac{1}{2}\sum_{k=0}^{N-1}[e_{[k]}^TQ_{[k]}e_{[k]}+u_{[k]}^TR_{[k]}u_{[k]}]\] \[J= \frac{1}{2}(C_zz_{[N]}) ^TS(C_zz_{[N]}) +\frac{1}{2}\sum_{k=0}^{N-1}[(C_zz_{[k]})^TQ_{[k]}C_zz_{[k]}+u_{[k]}^TR_{[k]}u_{[k]}]\] \[J= \frac{1}{2}z_{[N]}^{T}(C_z^TSC_z)z_{[N]} +\frac{1}{2}\sum_{k=0}^{N-1}[z_{[k]}^T(C_z^TQ_{[k]}C_z)z_{[k]}+u_{[k]}^TR_{[k]}u_{[k]}]\]
  • $S^z=C_z^TSC_z$
  • $Q^z=C_z^TQC_z$
\[J= \frac{1}{2}z_{[N]}^{T}(S^z)z_{[N]} +\frac{1}{2}\sum_{k=0}^{N-1}[z_{[k]}^TQ^z_{[k]}z_{[k]}+u_{[k]}^TR_{[k]}u_{[k]}]\]

According to LQR Gain ($x \to z$), the optimal control input:

\[u^\ast_{[N-k]}=-F_{[N-k]}z_{[N-k]}\]

where

\[F_{[N-k]}=(B^{T}P_{[k-1]}B+R)^{-1}B^{T}P_{[k-1]}A\]

Notice that the optimal control input is to regular the error $e$, not the augmented states $z$.

The optimal cost to go:

\[J_{N-k\to N}^{*}(z_{[N-k]})=\frac{1}{2}z_{[N-k]}^TP_{[k]}z_{[N-k]}\]

where

\[P_{[k]}=(A-BF_{[N-k]})^TP_{[k-1]}(A-BF_{[N-k]})+F_{[N-k]}^TRF_{[N-k]}+Q\] \[P_{[0]}=S^z\implies P_{[1]}, u^\ast_{[N-1]}\implies \cdots P_{[k]}, u^\ast_{[N-k]} \cdots \implies P_{[N]}, u^\ast_{[0]}\]

Test

Problem

Consider a simple system:

\[\begin{bmatrix} \dot x_1 \\ \dot x_2 \end{bmatrix}=\begin{bmatrix} 0 &1\\ 0 &0 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}+\begin{bmatrix}0\\ 1 \end{bmatrix}u(t)\] \[x^r(t)=\begin{bmatrix} 10\\ 0\\ \end{bmatrix}\]
  • weight matrix
\[Q=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, S=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, R=0.1\]

Simulation

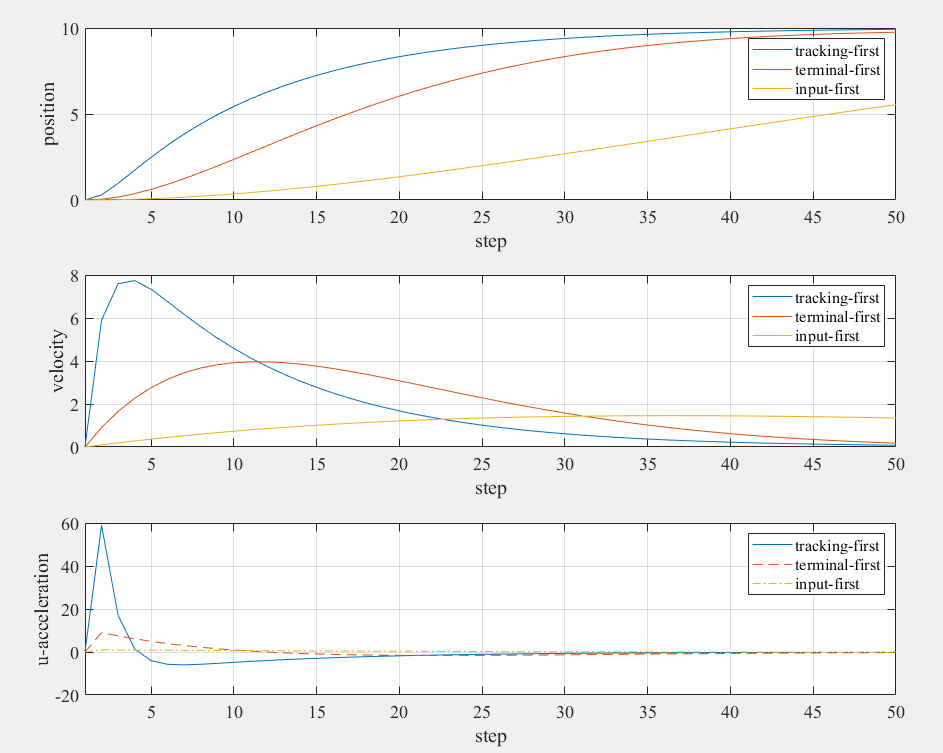
  • Consider a simple 2nd-order system:
\[\begin{bmatrix} \dot x_1 \\ \dot x_2 \end{bmatrix}=\begin{bmatrix} 0 &1\\ 0 &0 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}+\begin{bmatrix}0\\ 1 \end{bmatrix}u(t)\] \[x^r(t)=\begin{bmatrix} 10\\ 0\\ \end{bmatrix}\]
  • Tracking-first weight matrix
\[Q=\begin{bmatrix} 100 & 0 \\ 0 & 100 \end{bmatrix}, S=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, R=1\]
  • Terminal-first weight matrix
\[Q=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, S=\begin{bmatrix} 100 & 0 \\ 0 & 100 \end{bmatrix}, R=1\]
  • Input-first weight matrix
\[Q=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, S=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, R=100\]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153

%% LQR for regulator problem
%-----------------------------------------------%
% Youkoutaku:https://youkoutaku.github.io/
% Date: 2024/01/16
% Description: LQR for regulator problem. The constant reference signal is constant.
%-----------------------------------------------%
% LQR.m is a function to solve the LQR problem by dynamic programming.
% F = LQR(A,B,Q,R,S) solves the LQR problem.
clear;
close all;
clc;
set(0, 'DefaultAxesFontName', 'Times New Roman')
set(0, 'DefaultAxesFontSize', 14)

%% System Model
A = [0 1; 0 0];
n = size(A, 1);
B = [0; 1];
p = size(B, 2);
C = [1 0; 0 1];
D = [0; 0];

%% System Setting
Ts = 0.1; %Sample time
sys_d = c2d(ss(A, B, C, D), Ts); %discretization of continuous time system
A = sys_d.a; %discretized system matrix A
B = sys_d.b; %discretized input matrix B

%% Weight matrix
% tracking-first LQR
Q1 = [100 0; 0 100]; %R^(n x n) tracking error weight
S1 = [1 0; 0 1]; %R^(n x n) reference weight
R1 = 1; %R^(p x p) input weight

% terminal-first LQR
Q2 = [1 0; 0 1]; %R^(n x n) tracking error weight
S2 = [100 0; 0 100]; %R^(n x n) reference weight
R2 = 1; %R^(p x p) input weight

% Input-first LQR
Q3 = [1 0; 0 1]; %R^(n x n) tracking error weight
S3 = [1 0; 0 1]; %R^(n x n) reference weight
R3 = 100; %R^(p x p) input weight

%% Initial state
x0 = [0; 0];
x1 = x0;
x2 = x0;
x3 = x0;

%input init
u0 = 0;
u1 = u0;
u2 = u0;
u3 = u0;

%% Reference Signal
xr = [10; 2];
Ar = eye(n); % Augmented matrix

z1 = [x1; xr];
z2 = [x2; xr];
z3 = [x3; xr];

%% LQR Gain
Cz = [eye(n) -eye(n)];
Az = [A zeros(n); zeros(n) Ar];
Bz = [B; zeros(n, 1)];

Sz1 = Cz.' * S1 * Cz;
Qz1 = Cz.' * Q1 * Cz;
Sz2 = Cz.' * S2 * Cz;
Qz2 = Cz.' * Q2 * Cz;
Sz3 = Cz.' * S3 * Cz;
Qz3 = Cz.' * Q3 * Cz;

[F1] = LQR(Az, Bz, Qz1, R1, Sz1);
[F2] = LQR(Az, Bz, Qz2, R2, Sz2);
[F3] = LQR(Az, Bz, Qz3, R3, Sz3);

%% Simulation
k_steps = 50;
x_h1 = zeros(n, k_steps);
x_h2 = zeros(n, k_steps);
x_h3 = zeros(n, k_steps);
x_h1(:, 1) = x1;
x_h2(:, 1) = x2;
x_h3(:, 1) = x3;
u_h1 = zeros(p, k_steps);
u_h2 = zeros(p, k_steps);
u_h3 = zeros(p, k_steps);
u_h1(:, 1) = u1;
u_h2(:, 1) = u2;
u_h3(:, 1) = u3;

for k = 1:k_steps
	u1 =- F1 * z1;
	u2 =- F2 * z2;
	u3 =- F3 * z3;
	%System
	x1 = A * x1 + B * u1;
	x2 = A * x2 + B * u2;
	x3 = A * x3 + B * u3;
	x_h1(:, k + 1) = x1;
	x_h2(:, k + 1) = x2;
	x_h3(:, k + 1) = x3;
	u_h1(:, k + 1) = u1;
	u_h2(:, k + 1) = u2;
	u_h3(:, k + 1) = u3;
	z1 = [x1; xr];
	z2 = [x2; xr];
	z3 = [x3; xr];
end

%% figure
subplot(3, 1, 1);
plot(x_h1(1, :));
hold on;
plot(x_h2(1, :));
hold on;
plot(x_h3(1, :));
hold;
legend("tracking-first", "terminal-first", "input-first");
xlim([1, k_steps]);
xlabel("step")
ylabel("position")
grid on

subplot(3, 1, 2);
plot(x_h1(2, :));
hold on;
plot(x_h2(2, :));
hold on;
plot(x_h3(2, :));
hold;
legend("tracking-first", "terminal-first", "input-first");
xlim([1, k_steps]);
xlabel("step")
ylabel("velocity")
grid on

subplot(3, 1, 3);
plot(u_h1(1, :));
hold on;
plot(u_h2(1, :), '--');
hold on;
plot(u_h3(1, :), '-.');
hold;
legend("tracking-first", "terminal-first", "input-first");
xlim([1, k_steps]);
xlabel("step")
ylabel("u-acceleration")
grid on

Reference

Control Theory, Optimal Control
Optimal Control LQR Linear Quadratic Regulators
This post is licensed under CC BY 4.0 by the author.