カルマンフィルタ(Kalman filter)
Home Page:Youkoutaku
1.問題
スカラー変数のカルマンフィルタについて,観測雑音と システム雑音の分散を変化させ,これらと状態推定値 の精度およびカルマンゲインとの関係について,シミュ レーション例を通して考察しなさい
- 設定するパラメータ
- システム雑音の分散: $σ_w^2$
- 観測雑音の分散: $σ_2$
- 係数: $F=1, H=1$
- 初期値
- 状態推定値の初期値: $\overline{x}_0=0$
- 推定誤差分散の初期値: $v_0=σ^2$
2.カルマンフィルタ
状態遷移式:
\[x_k=Fx_{k-1}+w\]- $w=N(w | 0,σ_w^2)$ : システム雑音
- $x_k$: 時刻 $t_k$ におけるシステム状態 $x$
観測モデル:
\(y_k=Hx_{k}+ϵ\)
- $ϵ=N(ϵ |0, \sigma^2)$: 観測雑音
- $y_k$: 時刻 $t_k$ における観測値 $y$
- 設定するパラメータ
システム雑音の分散: $σ_w^2$
観測雑音の分散: $σ^2$
係数: $F, H$ \ - 初期値
状態変数の初期値:$x_0$
状態推定値の初期値: $\overline{x}_0$
事後分布の分散の初期値:$v_0$
時間更新式:
\[\begin{aligned}&p_{k-1}=F^{2}v_{k-1}+\sigma_{W}^{2}\\&{v}_{k}=(1-\kappa H)p_{k-1}\\& {x}_{k}=F \bar{x}_{k-1}+\kappa(y_{k}-HF \bar{x}_{k-1})\end{aligned}\]カルマンゲイン:
\[\kappa=\frac{p_{k-1}H}{\sigma^2+H^2p_{k-1}}\]3.プログラム
3.1 ライブラリのインポートと関数定義
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 以下のライブラリを使うので、あらかじめ読み込んでおいてください
import numpy as np
import scipy as sp
import pandas as pd
from pandas import Series, DataFrame
# 可視化ライブラリ
import matplotlib.pyplot as plt
import matplotlib as mpl
#import seaborn as sns
%matplotlib inline
# 小数第3位まで表示
%precision 3
#カルマンフィルタ
def kf_scalar(F,H,Q,R,y,xhat,V):
#カルマンフィルタの更新を行う
P=F*F*V+Q; #①誤差分散p(k-1)
G=P*H/(H*H*P+R); #②カルマンゲインχ
V=(1-G*H)*P; #③事後分布の分散行列(v(k))
xhat=F*xhat+G*(y-H*F*xhat); #③推定値(x(k)-)
return(xhat, V, G);
3.2 パラメータ設定
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
F=1; H=1; #係数
sigma_w=2.0; #システム雑音の標準偏差(σw)
sigma=2.0; #観測雑音の標準偏差(σ)
Q=sigma_w**2; #システム雑音の分散(σw^2)
R=sigma**2; #観測雑音の分散(σ^2)
K=300; #データ数
#初期値の設定
x=0.0; #状態量の初期値(x0)
xhat= 0.0; #状態推定値の初期値(x0-)
V=0; #事後分布の分散の初期値(v0)
# ランダムシードの固定
np.random.seed(0)
3.3 シミュレーション
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
result=[]
for k in range(0,K):
#雑音信号の生成:np.random.normal(平均、標準偏差)
w = np.random.normal(0, sigma_w); #システム雑音(w)
v = np.random.normal(0, sigma); #観測雑音(v)
#xの真値の計算
x = F*x + w;
#観測値yの計算
y = H*x + v;
#カルマンフィルタによる状態推定
xhat, V ,G = kf_scalar(F,H,Q,R,y,xhat,V);
result.append([k, x, y, xhat, V, G])
df=DataFrame(data=result, columns=['k','x','y','xhat','V','G'])
1
df
| k | x | y | xhat | V | G | |
|---|---|---|---|---|---|---|
| 0 | 0 | 3.528105 | 4.328419 | 2.164210 | 2.000000 | 0.500000 |
| 1 | 1 | 5.485581 | 9.967367 | 6.846104 | 2.400000 | 0.600000 |
| 2 | 2 | 9.220697 | 7.266141 | 7.104588 | 2.461538 | 0.615385 |
| 3 | 3 | 11.120873 | 10.818159 | 9.398264 | 2.470588 | 0.617647 |
| 4 | 4 | 10.914436 | 11.735633 | 10.842706 | 2.471910 | 0.617978 |
| ... | ... | ... | ... | ... | ... | ... |
| 295 | 295 | -48.742807 | -47.864721 | -49.795159 | 2.472136 | 0.618034 |
| 296 | 296 | -49.181889 | -51.349962 | -50.756080 | 2.472136 | 0.618034 |
| 297 | 297 | -48.478329 | -47.719858 | -48.879592 | 2.472136 | 0.618034 |
| 298 | 298 | -49.418395 | -49.851858 | -49.480485 | 2.472136 | 0.618034 |
| 299 | 299 | -51.278708 | -51.635886 | -50.812596 | 2.472136 | 0.618034 |
300 rows × 6 columns
3.4 描画
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#推定結果の描画
fig, axes = plt.subplots(nrows=4, ncols=1, figsize=(10, 15))
df.plot(ax=axes[0],x='k', y=['x','xhat','y'], color=["black","red","green"] )
axes[0].set_xlabel("k")
axes[0].set_ylabel("x, xhat, y")
axes[0].set_xlim(0, K)
axes[0].set_ylim(-60, 40)
axes[0].grid(True)
df.plot(ax=axes[1],x='k', y=['x','xhat'], color=["black","red"] )
axes[1].set_xlabel("k")
axes[1].set_ylabel("x, xhat")
axes[1].set_xlim(0, K)
axes[1].set_ylim(-60, 40)
axes[1].grid(True)
#カルマンゲインの描画
df.plot(ax=axes[2],x='k', y='G', color="red" )
axes[2].set_xlabel("k")
axes[2].set_ylabel("Kalman gain")
axes[2].set_xlim(0, K)
axes[2].set_ylim(0, 1)
axes[2].grid(True)
#推定誤差分散の描画
df.plot(ax=axes[3],x='k', y='V', color="blue" )
axes[3].set_xlabel("k")
axes[3].set_ylabel("estimate error variance")
axes[3].set_xlim(0, K)
axes[3].set_ylim(0, 3)
axes[3].grid(True)
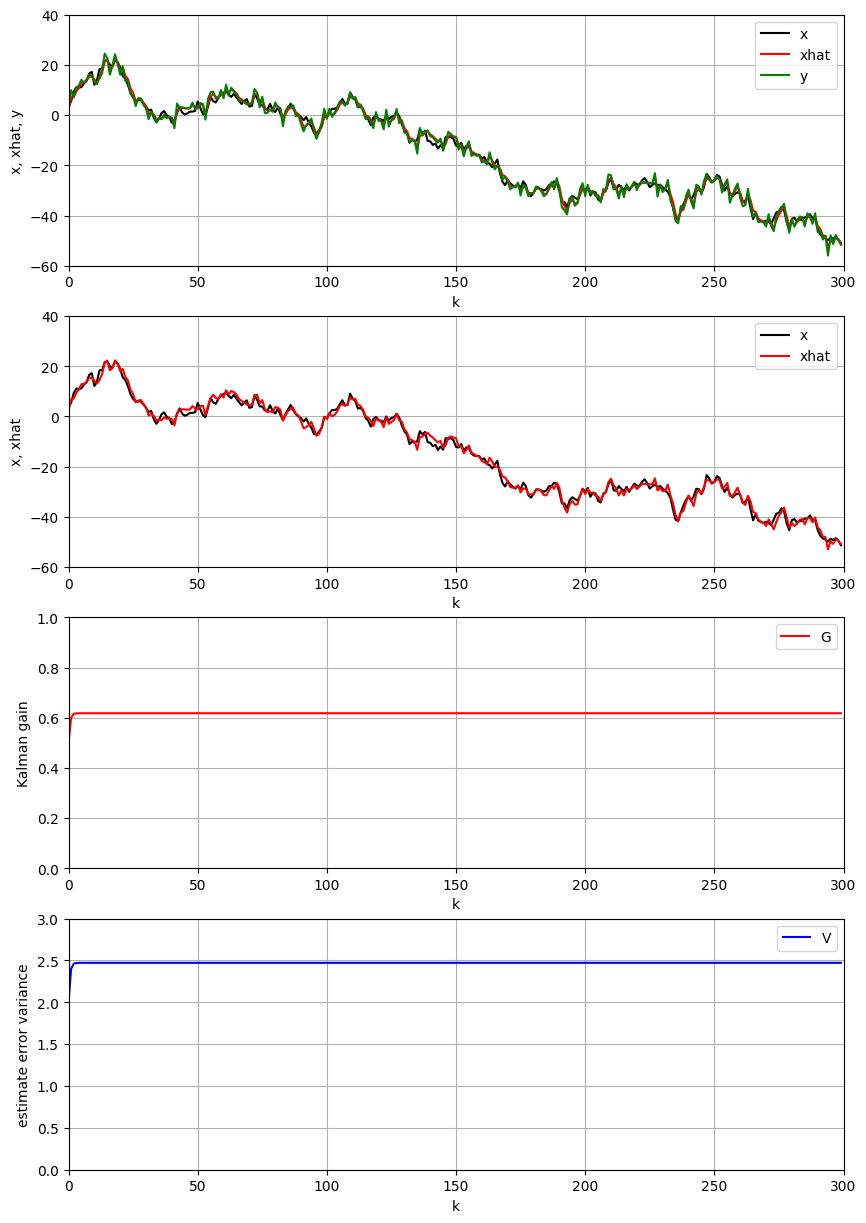
4.考察
4.1 $σ_w$
システム雑音の標準偏差 $σ_w=15$ と観測雑音の標準偏差 $σ=2$ と設定する.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#-----------------------------------------
# パラメータの設定
#-----------------------------------------
F=1; H=1; #係数
sigma_w=15.0; #システム雑音の標準偏差(σw)
sigma=2.0; #観測雑音の標準偏差(σ)
Q=sigma_w**2; #システム雑音の分散(σw^2)
R=sigma**2; #観測雑音の分散(σ^2)
K=300; #データ数
#初期値の設定
x=0.0; #状態量の初期値(x0)
xhat= 0.0; #状態推定値の初期値(x0-)
V=0; #事後分布の分散の初期値(v0)
result=[]
for k in range(0,K):
#雑音信号の生成:np.random.normal(平均、標準偏差)
w = np.random.normal(0, sigma_w); #システム雑音(w)
v = np.random.normal(0, sigma); #観測雑音(v)
#xの真値の計算
x = F*x + w;
#観測値yの計算
y = H*x + v;
#カルマンフィルタによる状態推定
xhat, V ,G = kf_scalar(F,H,Q,R,y,xhat,V);
result.append([k, x, y, xhat, V, G])
df_1=DataFrame(data=result, columns=['k','x','y','xhat','V','G'])
1
df_1
| k | x | y | xhat | V | G | |
|---|---|---|---|---|---|---|
| 0 | 0 | -23.256440 | -22.421803 | -22.030155 | 3.930131 | 0.982533 |
| 1 | 1 | -37.421968 | -36.945761 | -36.689623 | 3.931310 | 0.982827 |
| 2 | 2 | -58.511411 | -59.691527 | -59.296528 | 3.931310 | 0.982828 |
| 3 | 3 | -60.168752 | -63.490152 | -63.418137 | 3.931310 | 0.982828 |
| 4 | 4 | -58.441534 | -59.199829 | -59.272268 | 3.931310 | 0.982828 |
| ... | ... | ... | ... | ... | ... | ... |
| 295 | 295 | 290.495100 | 292.742911 | 292.757904 | 3.931310 | 0.982828 |
| 296 | 296 | 287.893142 | 286.873083 | 286.974139 | 3.931310 | 0.982828 |
| 297 | 297 | 308.780918 | 310.856090 | 310.445978 | 3.931310 | 0.982828 |
| 298 | 298 | 309.062795 | 307.875240 | 307.919386 | 3.931310 | 0.982828 |
| 299 | 299 | 278.884591 | 280.063998 | 280.542343 | 3.931310 | 0.982828 |
300 rows × 6 columns
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#推定結果の描画
fig, axes = plt.subplots(nrows=4, ncols=1, figsize=(10, 15))
df_1.plot(ax=axes[0],x='k', y=['x','xhat','y'], color=["black","red","green"] )
axes[0].set_xlabel("k")
axes[0].set_ylabel("x, xhat, y")
axes[0].set_xlim(0, K)
axes[0].set_ylim(-300, 150)
axes[0].grid(True)
df_1.plot(ax=axes[1],x='k', y=['x','xhat'], color=["black","red"] )
axes[1].set_xlabel("k")
axes[1].set_ylabel("x, xhat")
axes[1].set_xlim(0, K)
axes[1].set_ylim(-300, 150)
axes[1].grid(True)
#カルマンゲインの描画
df_1.plot(ax=axes[2],x='k', y='G', color="red" )
axes[2].set_xlabel("k")
axes[2].set_ylabel("Kalman gain")
axes[2].set_xlim(0, K)
axes[2].set_ylim(0, 1.5)
axes[2].grid(True)
#推定誤差分散の描画
df_1.plot(ax=axes[3],x='k', y='V', color="blue" )
axes[3].set_xlabel("k")
axes[3].set_ylabel("estimate error variance")
axes[3].set_xlim(0, K)
axes[3].set_ylim(0, 5)
axes[3].grid(True)
上の結果により,システム雑音の標準偏差が観測雑音の標準偏差より大きい場合に,カルマンフィルタゲインが大きくなり,推定性能が良くなることがわかる.
- カルマンフィルタゲインについて2のカルマンフィルタの説明によって次の式が得られる。 \(\kappa=\frac{p_{k-1}H}{\sigma^2+H^2p_{k-1}}=\frac{(F^{2}v_{k-1}+\sigma_{W}^{2})H}{\sigma^2+(F^{2}v_{k-1}+\sigma_{W}^{2})H^2}=\frac{H}{\frac{\sigma^2}{(F^{2}v_{k-1}+\sigma_{W}^{2})}+H^2}\)
よって,$σ_w$が大きいほど,カルマンフィルタゲイン$\kappa$が大きいことが解析の通りである.
- カルマンフィルタゲインが大きいため,時間更新式の推定値$x_k$ における観測値の重要さが高くなり,システムモデルによる事前予測値の重要さが低くなる.
- システム雑音の標準偏差が高いため,システムモデルによる事前予測値のバラツキが大きい.観測雑音の標準偏差が小さいため,観測値のバラツキが小さい.そのために,事前予測値より,観測値の方は信頼度が高い.
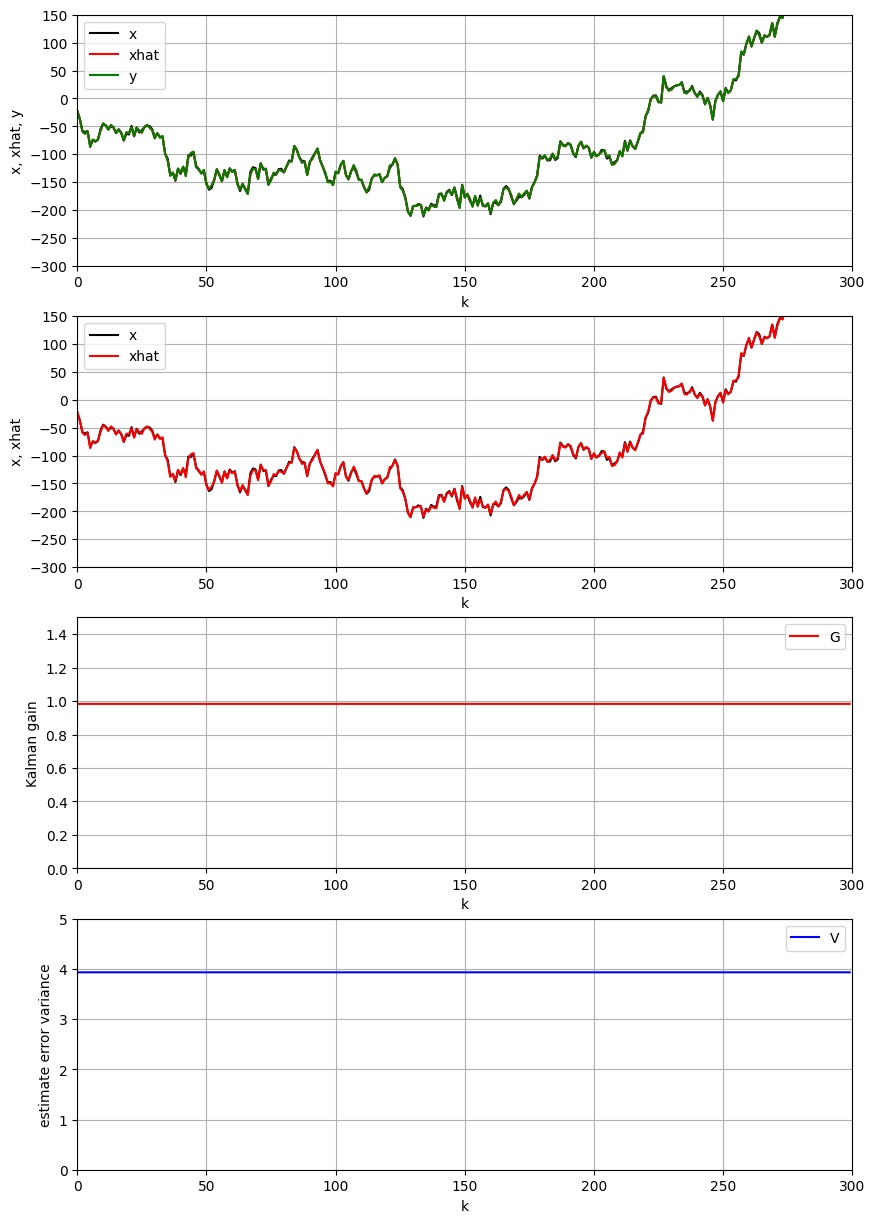
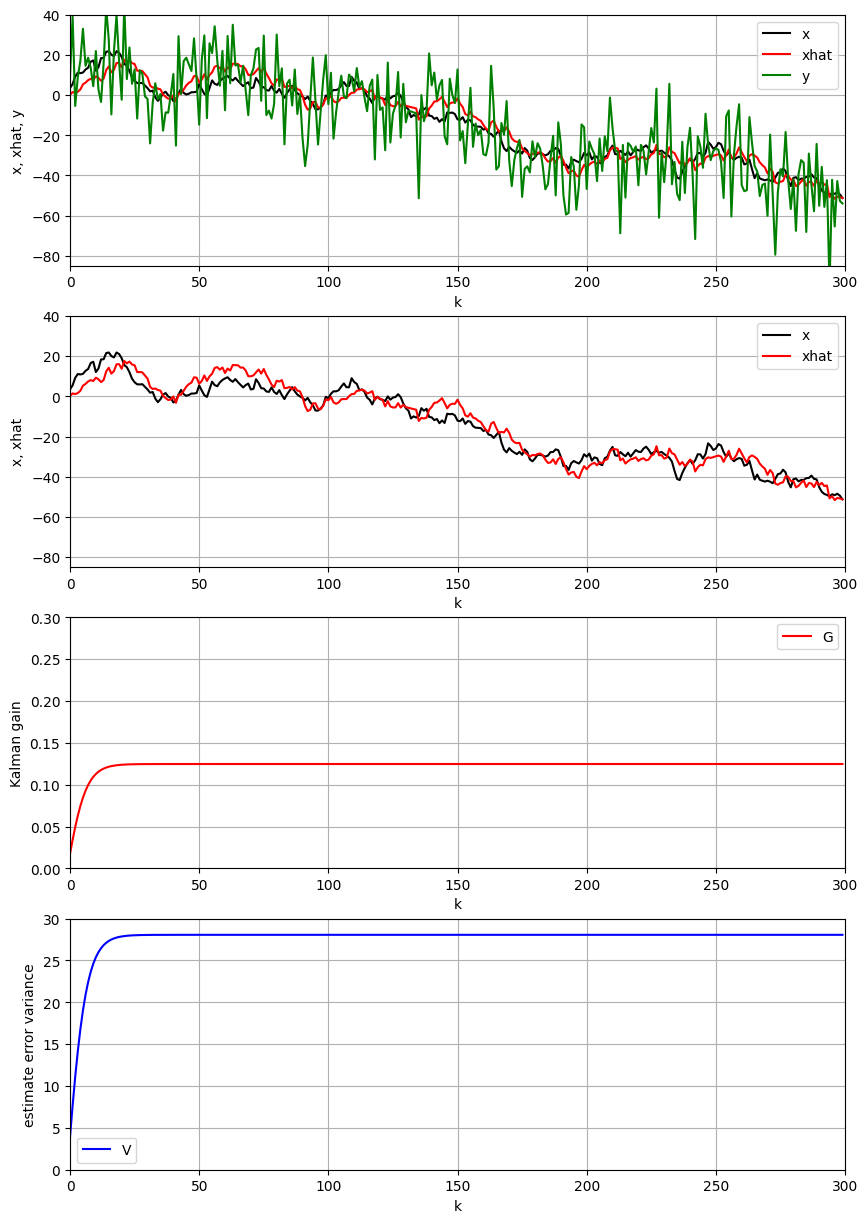
4.2 $σ^2$
システム雑音の標準偏差 $σ_w=2$ と観測雑音の標準偏差 $σ=15$ と設定する.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#-----------------------------------------
# パラメータの設定
#-----------------------------------------
F=1; H=1; #係数
sigma_w=2.0; #システム雑音の標準偏差(σw)
sigma=15.0; #観測雑音の標準偏差(σ)
Q=sigma_w**2; #システム雑音の分散(σw^2)
R=sigma**2; #観測雑音の分散(σ^2)
K=300; #データ数
#初期値の設定
x=0.0; #状態量の初期値(x0)
xhat= 0.0; #状態推定値の初期値(x0-)
V=0; #事後分布の分散の初期値(v0)
# ランダムシードの固定
np.random.seed(0)
result=[]
for k in range(0,K):
#雑音信号の生成:np.random.normal(平均、標準偏差)
w = np.random.normal(0, sigma_w); #システム雑音(w)
v = np.random.normal(0, sigma); #観測雑音(v)
#xの真値の計算
x = F*x + w;
#観測値yの計算
y = H*x + v;
#カルマンフィルタによる状態推定
xhat, V ,G = kf_scalar(F,H,Q,R,y,xhat,V);
result.append([k, x, y, xhat, V, G])
df_2=DataFrame(data=result, columns=['k','x','y','xhat','V','G'])
1
df_2
| k | x | y | xhat | V | G | |
|---|---|---|---|---|---|---|
| 0 | 0 | 3.528105 | 9.530463 | 0.166471 | 3.930131 | 0.017467 |
| 1 | 1 | 5.485581 | 39.098979 | 1.491932 | 7.660149 | 0.034045 |
| 2 | 2 | 9.220697 | -5.438472 | 1.150474 | 11.085658 | 0.049270 |
| 3 | 3 | 11.120873 | 8.850515 | 1.634302 | 14.137759 | 0.062834 |
| 4 | 4 | 10.914436 | 17.073413 | 2.786040 | 16.784706 | 0.074599 |
| ... | ... | ... | ... | ... | ... | ... |
| 295 | 295 | -48.742807 | -42.157163 | -49.681037 | 28.066593 | 0.124740 |
| 296 | 296 | -49.181889 | -65.442438 | -51.647121 | 28.066593 | 0.124740 |
| 297 | 297 | -48.478329 | -42.789796 | -50.542254 | 28.066593 | 0.124740 |
| 298 | 298 | -49.418395 | -52.669367 | -50.807591 | 28.066593 | 0.124740 |
| 299 | 299 | -51.278708 | -53.957544 | -51.200518 | 28.066593 | 0.124740 |
300 rows × 6 columns
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#推定結果の描画
fig, axes = plt.subplots(nrows=4, ncols=1, figsize=(10, 15))
df_2.plot(ax=axes[0],x='k', y=['x','xhat','y'], color=["black","red","green"] )
axes[0].set_xlabel("k")
axes[0].set_ylabel("x, xhat, y")
axes[0].set_xlim(0, K)
axes[0].set_ylim(-85, 40)
axes[0].grid(True)
df_2.plot(ax=axes[1],x='k', y=['x','xhat'], color=["black","red"] )
axes[1].set_xlabel("k")
axes[1].set_ylabel("x, xhat")
axes[1].set_xlim(0, K)
axes[1].set_ylim(-85, 40)
axes[1].grid(True)
#カルマンゲインの描画
df_2.plot(ax=axes[2],x='k', y='G', color="red" )
axes[2].set_xlabel("k")
axes[2].set_ylabel("Kalman gain")
axes[2].set_xlim(0, K)
axes[2].set_ylim(0, 0.3)
axes[2].grid(True)
#推定誤差分散の描画
df_2.plot(ax=axes[3],x='k', y='V', color="blue" )
axes[3].set_xlabel("k")
axes[3].set_ylabel("estimate error variance")
axes[3].set_xlim(0, K)
axes[3].set_ylim(0, 30)
axes[3].grid(True)
上の結果により,システム雑音の標準偏差が観測雑音の標準偏差より小さい場合に,カルマンフィルタゲインが小さくなり,推定性能が悪くなることがわかる.
- カルマンフィルタゲインの式により,
よって,$σ$が大きいほど,カルマンフィルタゲイン$\kappa$が小さいことが解析の通りである.
- カルマンフィルタゲインが小さいため,時間更新式の推定値 $x_k$ における観測値の重要さが低くなり,システムモデルによる事前予測値の重要さが高くなる.
- システム雑音の標準偏差が低いため,システムモデルによる事前予測値のバラツキが小さい.観測雑音の標準偏差が小さいため,観測値のバラツキが大きい.そのために,観測値より,事前予測値の方は信頼度が高い.
This post is licensed under CC BY 4.0 by the author.