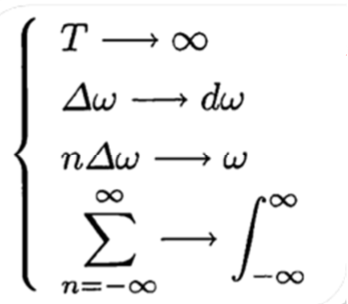Fourier transform
2.3 フーリエ級数からフーリエ変換
複素フーリエ級数 の$c_n$を$f(t)$に代入すると,
\[f(t)=\sum_{-\infty}^{\infty} [\frac 1T\int_{-\frac T2}^{\frac T2} f(t)e^{-j2\pi \frac nT t}dt]e^{ 2\pi \frac nt T}\]基本周波数を$\omega_0$とすると,
\[\frac {1}{T}=\frac {\omega_0}{2\pi}\] \[f(t)=\frac {1}{2\pi}\sum_{-\infty}^{\infty} [{\omega_0}\int_{-\frac T2}^{\frac T2} f(t)e^{-jn{\omega_0} t}dt]e^{jn{\omega_0} t}\]周期$T$が非常に大きいと,基本角周波数は非常に小さくなり,$\omega_0= {\Delta} \omega$と表す.
\[f(t)=\frac {1}{2\pi}\int_{-\infty}^{\infty} \left[\int_{-\infty}^{\infty} f(t)e^{-j\omega t}dt \right]e^{j\omega t}d\omega\]2.4 フーリエ変換
\[F(\omega)=\int_{-\infty}^{\infty} f(t)e^{-j\omega t}dt\]独立波を扱う
2.5 逆フーリエ変換
\[f(t)=\frac 1{2\pi} \int_{-\infty}^{\infty} F(\omega)e^{j\omega t}d\omega\]2.6 フーリエ変換の性質
Linearity
\[\mathcal{F}[af(t)+bf(t)]=aF(\omega)+bF(\omega)\]波形の移動(時間軸の推移)
\[\mathcal{F}[f(t-\tau)]=e^{-j\omega\tau}F(\omega)\]周波数軸方向の移動(周波数の推移)
\[\mathcal{F}[f(t)e^{j\omega_0t}]=F(\omega-\omega_0)\]相対性
逆フーリエ変換において,両辺を$2\pi$をかけ,$\omega\to t$, $t\to-\omega$の入れ替えを行うと,
\[f(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}F(\omega)e^{j\omega t}d\omega \to 2\pi f(-\omega)=\int_{-\infty}^{\infty}F(t)e^{jt(-\omega)}dt\] \[2\pi f(-\omega) \iff F(t)\] This post is licensed under CC BY 4.0 by the author.