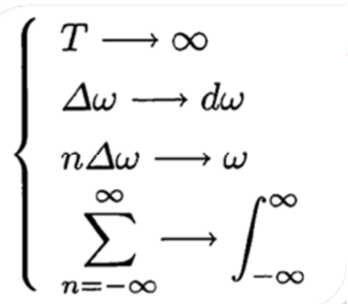Fourier transform

2.3 フーリエ級数からフーリエ変換

複素フーリエ級数 の$c_n$を$f(t)$に代入すると，

\[f(t)=\sum_{-\infty}^{\infty} [\frac 1T\int_{-\frac T2}^{\frac T2} f(t)e^{-j2\pi \frac nT t}dt]e^{ 2\pi \frac nt T}\]

基本周波数を$\omega_0$とすると，

\[\frac {1}{T}=\frac {\omega_0}{2\pi}\] \[f(t)=\frac {1}{2\pi}\sum_{-\infty}^{\infty} [{\omega_0}\int_{-\frac T2}^{\frac T2} f(t)e^{-jn{\omega_0} t}dt]e^{jn{\omega_0} t}\]

周期$T$が非常に大きいと，基本角周波数は非常に小さくなり，$\omega_0= {\Delta} \omega$と表す．

\[f(t)=\frac {1}{2\pi}\int_{-\infty}^{\infty} \left[\int_{-\infty}^{\infty} f(t)e^{-j\omega t}dt \right]e^{j\omega t}d\omega\]

2.4 フーリエ変換

\[F(\omega)=\int_{-\infty}^{\infty} f(t)e^{-j\omega t}dt\]

独立波を扱う

2.5 逆フーリエ変換

\[f(t)=\frac 1{2\pi} \int_{-\infty}^{\infty} F(\omega)e^{j\omega t}d\omega\]

2.6 フーリエ変換の性質

Linearity

\[\mathcal{F}[af(t)+bf(t)]=aF(\omega)+bF(\omega)\]

波形の移動（時間軸の推移）

\[\mathcal{F}[f(t-\tau)]=e^{-j\omega\tau}F(\omega)\]

周波数軸方向の移動（周波数の推移）

\[\mathcal{F}[f(t)e^{j\omega_0t}]=F(\omega-\omega_0)\]

相対性

逆フーリエ変換において，両辺を$2\pi$をかけ，$\omega\to t$, $t\to-\omega$の入れ替えを行うと，

\[f(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}F(\omega)e^{j\omega t}d\omega \to 2\pi f(-\omega)=\int_{-\infty}^{\infty}F(t)e^{jt(-\omega)}dt\] \[2\pi f(-\omega) \iff F(t)\]