Filter
信号処理における フィルタ とは,信号の 周波数特性 を操作するものであり,信号の不要な周波数成分を除去したり減衰したりして,必要な周波数成分のみからなる信号を得る処理をするものである.
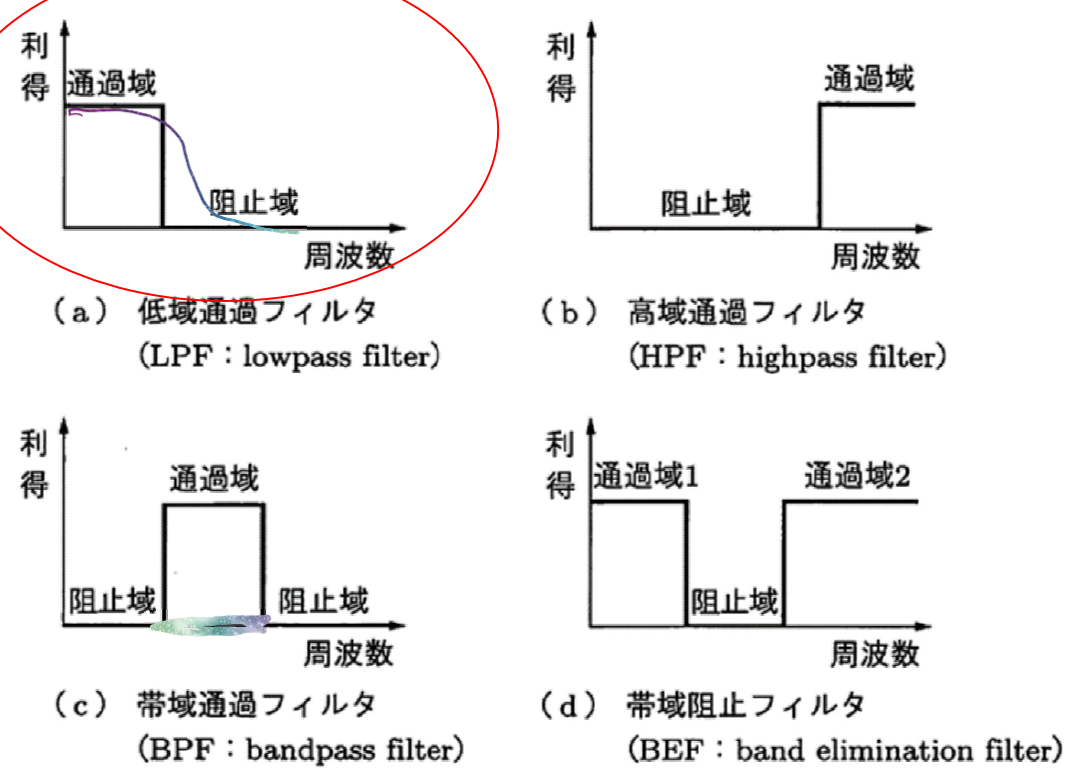
8.1 フィルタ種類
- ★ LPF (lowpass filter, 低域通過フィルタ)
- HPF(highpass filter, 高域通過フィルタ)
- BPF(bandpass filter, 帯域通過フィルタ)
- BEF(band elimination filter, 帯域阻止フィルタ)
理想的なフィルタとは,
- (1)通過域で利得(ゲン)が一定であること
- (2)過渡域での傾きが急峻であること
- (3)阻止域の利得が 0 であること
- (4)直線位相であること,つまり,通過域で位相特性が周波数に比例しれ直線的に変換すること.
8.2 アナログフィルタ 設計
フィルタ設計のステップ
- (1) フィルタの近似所望の特性をもつ伝達関数を設計する.
- (2)回路実現求められた伝達関数を抵抗やコンデンサ,コイルmオペアンプなどの素子を用いて回路として実現する.
フィルタの設計は LPF 低域通過フィルタが基本となっている.
代表的なフィルタ
- 一次遅れ系によるフィルタ
- バターワースフィルタ(Butterworth filter)
- チェビシェフフィルタ
8.3★ バターワースフィルタ
- まず,周波数特性 $|H(\omega)|^2$ を決める(次数 $N$ , 遮断周波数 $\omega_c$)
バターワースフィルタ:
\[|H(\omega)|^2=\frac {1}{1+{(\omega/\omega_c)}^{2N}}\]そして,連続時間伝達関数の絶対値の 2 乗 $|H(s)|^2$ を得るために,$s=j\omega$ を代入すると,
\[|H(s)|^2=|H(\omega)|^2_{\omega=s/j}=\frac {1}{1+(-j)^{2N} {(s/\omega_c)}^{2N}}=\frac {1}{1+(-1)^{2N}(j^2)^N {(s/\omega_c)}^{2N}}\] \[=\frac {1}{1+(-1)^{N} {(s/\omega_c)}^{2N}}\]Filter の極を求めるために,分母=0 とすると,
\[(-1)^{N} {(s/\omega_c)}^{2N}=-1\]が得られる.
複素数の n 乗根: $\omega=R(\cos\alpha+j\sin\alpha)$ >$s=r(\cos\theta+j\sin\theta)$ >$s^n=r^n(\cos{n\theta}+j\sin{n\theta})=R(\cos\alpha+j\sin\alpha)$ よって, $r=R^{1/n}$ >$n\theta=\alpha+2\pi k, (k=0,1,\dots,n-1)$ ==n 個根である.== 以上で, $s=\omega^{1/n}=R^{1/n} [\cos (\frac {\alpha+2\pi k}{n} ) +j\sin (\frac {\alpha+2\pi k}{n} )], (k=0,1,\dots,n-1))$
- a) N が偶数の場合
従って,$2N$ 個の根
\[s_k={\omega_c}・e^{\frac {j(\pi+2k\pi)}{2N}}, k=0,1,\dots,2N-1\]- b) N が奇数の場合
従って,$2N$ 個の根
\[s_k={\omega_c}・e^{j\frac {k\pi}{N}}, k=0,1,\dots,2N-1\]伝達関数を求める. 安定の根 $s_k$ を選択する(実数部が負数) \(H(s)=\frac {1}{(s-s_i)(s-s_j)\dots}\)
8.4 ★ 周波数変換
実際にフィルタを設定する時に,LPF フィルタを分かれば,ほかのフィルタに変換できる.
遮断周波数 の変換(LPF)
\[s→\frac s{\omega_1}\]通過域$[0,\omega_1], \omega_1$:LPF の遮断周波数
HPF へ
\[s→\frac {\omega_h}{s}\]通過域$[\omega_h,\infty], \omega_h$:HPF の遮断周波数
BPF へ
\[s→\frac {s^2+{\omega_1}{\omega_2}}{B_\omega s}\]通過域$[\omega_1,\omega_2], B_\omega$: 帯域幅
BEF へ
\[s→\frac {B_\omega s}{s^2+{\omega_1}{\omega_2}}\]通過域$[\omega_1,\omega_2], B_\omega$: 帯域幅