Discrete-time Systems
6.1 サンプリング定理(標本化定理)
サンプリング定理 または,標本化定理とも呼ばれる.シャノンの標本化定理
信号成分の最大周波数の 2 倍より高いサンプリング周波数を取るべきだ.
信号 $x(t)$ の成分の最大(角)周波数 $\omega_M$ が $\omega_M<\omega_s/2=T/\pi$ を満足するとき,サンプリング定理を満たす.
\[\omega_s>2\omega_M\]6.2 ★ 伝達関数
線形な離散時間システム の出力は,これまでの出力と入力を用いて,一般的に以下のような線形差分方程式で表すことができる.
\[y(n)+a_1y(n-1)+a_2y(n-2)+\dots+a_Iy(n-I)\] \[=b_0x(n)+b_1x(n-1)+b_2x(n-2)+\dots+b_Jx(n-I)\]初期値を 0 として, z 変換 すると,
\[Y(z)+a_1Y(z)z^{-1}+a_2Y(z)z^{-2}+\dots+a_IY(z)z^{-I}\] \[=b_0X(z)+b_1X(z)z^{-1}+b_2X(z)z^{-2}+\dots+b_JX(z)z^{-J}\]となる.従って,
\[\frac {Y(z)}{X(Z)}=H(z)=\frac {b_0+b_1z^{-1}+b_2z^{-2}+\dots+b_Jz^{-J}}{1+a_1z^{-1}+a_2z^{-2}+\dots+a_Iz^{-I}}\]これは, 離散時間システムの伝達関数 という.分子多項式= 0 を満たす z を 零点 という.分母多項式=0 を満たす z を 極 という.
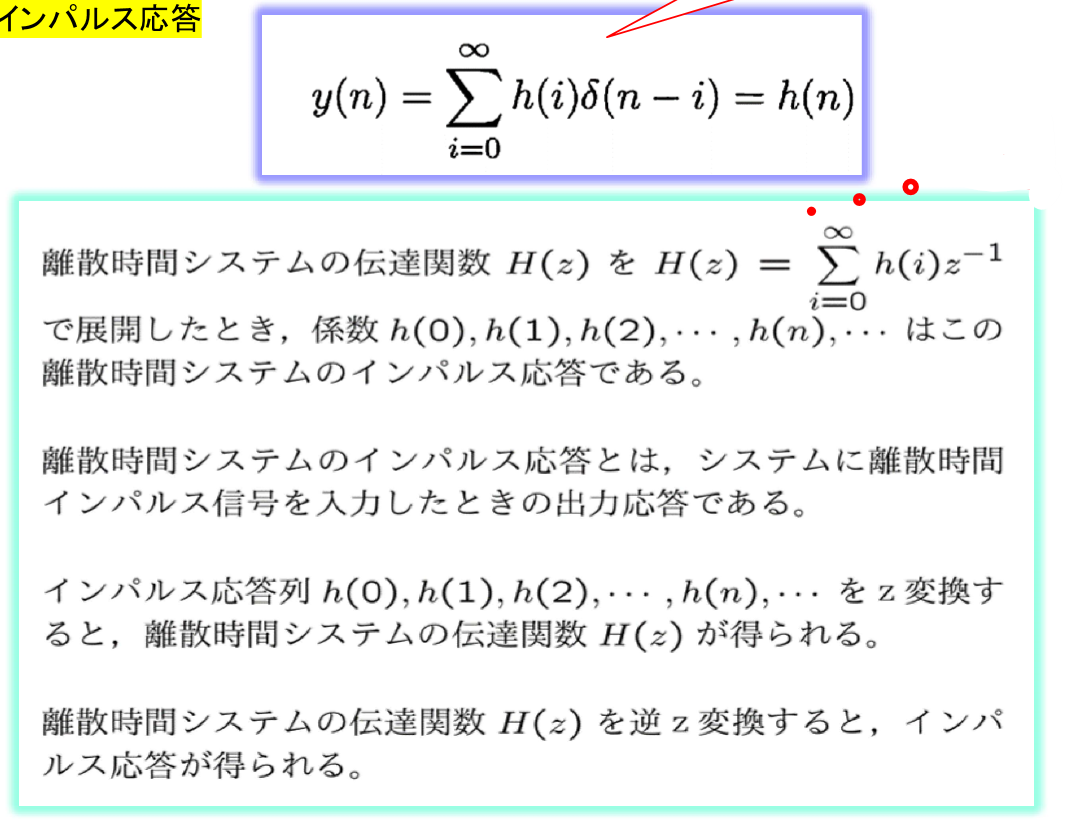
6.3 ★ インパルス応答
連続時間システムのインパルス応答 :入力 $u(t)=δ(t)$ を Laplace Transforms による 微分方程式 に代入すると,出力 $Y(s)=$ 伝達関数 $H(s)$.つまり,連続時間システムのインパルス応答 $y(t)$ は, 伝達関数の逆ラプラス変換 $h(t)$. 連続時間システムの伝達関数 は, インパルス応答のラプラス変換 $Y(s)$.
離散時間システムのインパルス応答:
6.4 巡回型システムと非巡回型
IIR
- (infinite impiles response, 無限インパルス応答) 伝達関数 $H(z)$ が分母があると, 巡回型システム である.
FIR
- (finite impilse repose, 有限インパルス応答) 伝達関数 $H(z)$ が分母がないと, 非巡回型システム である.
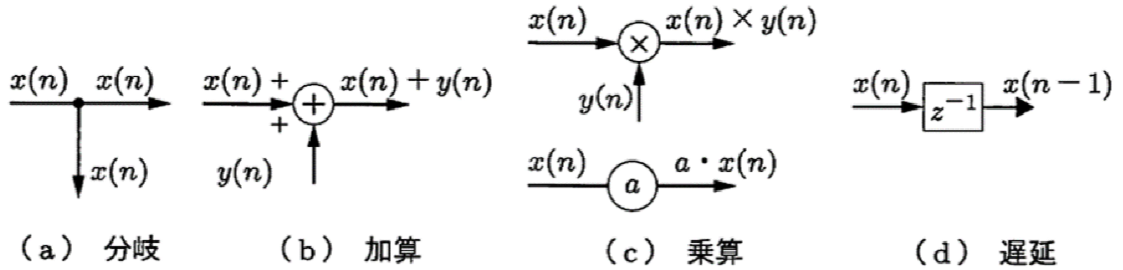
6.5 ディジタル信号処理での基本要素
6.6 ★ 離散時間畳み込み(時間域)
\[y(n)=\sum_{k=-\infty}^{\infty} x(k)h(n-k)\]因果律に注意する!
入力信号のみが因果律を満たす場合:
\[y(n)=\sum_{k=0}^{\infty} x(k)h(n-k)\]システムのみが因果律を満たす場合:
\[y(n)=\sum_{k=-\infty}^{n} x(k)h(n-k)\]入力信号とシステムの両方が因果律を満たす場合:
\[y(n)=\sum_{k=0}^{n} x(k)h(n-k)\]たたみ込みの対称性:
\[y(n)=\sum_{k=0}^{n} x(k)h(n-k)=\sum_{k=0}^{n} x(n-k)h(k)\]
6.7 離散時間たたみ込みの意味
6.8 ★ 周波数応答
周波数領域変換 $H(z)$ に代入する
\[z=e^{jωT}\] \[H(e^{j\omega T})=|H(e^{j\omega T})| e^{j\theta}\]
振幅特性
\[|H(e^{j\omega T})|=\sqrt{[Re\{H(e^{j\omega T}\}]^2+[Im\{H(e^{j\omega T}\}]^2}\]位相特性
\[\theta(\omega)=arg(H(e^{j\omega T}))=tan^-1[\frac {Im\{H(e^{j\omega T})\}}{Re\{H(e^{j\omega T})\}}]\]群遅延
\[\tau(\omega)=- \frac {\partial\theta(\omega)}{\partial\omega}\]6.9 ★ 離散時間システム の 安定性
連続時間システム:
\[G(s) →G(j\omega), s=j\omega\]離散時間システム:
\[H(z)→H(e^{j\omega T}), z=e^{j\omega T}\]よって,
\[z=e^{sT}=e^{j\omega T}\]$s=\sigma+j\omega,\sigma=0$ ⇒ $|e^{j\omega T}|=1$ s 平面の虚数軸は,z 平面の単位円に 写像される.
- 安定 すべての極の絶対値が 1 より小さい
- 安定限界 極の絶対値が 1 を満たす
- 不安定 極の絶対値が 1 より大きい
This post is licensed under CC BY 4.0 by the author.