Continuous-time signal sampling

2.1 連続時間信号のサンプリングとサンプリング定理

• $T:$ サンプリング周期
• $\omega:$ サンプリング角周波数

1.連続時間信号のサンプリング(サンプル値信号)離散時間信号

\[x_{p}(t)=x(t)p(t)=\sum_{n=-\infty}^{\infty}x(nT)\delta(t-nT)\]

インパルス列（サンプリング関数）

\[p(t)=\sum_{n=-\infty}^{\infty}\delta(t-nT)\]

インパルス列は周期関数なので，その複素フーリエ級数は，

\[c_k=\frac{1}{T}\int_{-T/2}^{T/2}\delta(t)e^{-j\frac{2\pi}{T}kt}dt\] \[p(t)=\sum_{k=-\infty}^{\infty}c_ke^{j\frac{2\pi}{T}kt}=\sum_{k=-\infty}^{\infty}\frac{1}{T}e^{j\frac{2\pi}{T}kt}\]

である．そして,フーリエ変換すると，

\[P(\omega)=\int_{-\infty}^{\infty}\sum_{k=-\infty}^{\infty}\frac{1}{T}e^{j\frac{2\pi}{T}kt}e^{-j\omega t}dt=\sum_{k=-\infty}^{\infty}\frac{1}{T}\int_{-\infty}^{\infty}e^{-j(\omega-k\omega_s)t}dt\]

デルタ関数のフーリエ変換により，

\[\delta(\omega)=\frac{1}{2\pi}\int_{-\infty}^{\infty}e^{j\omega t}dt\]

よって，(デルタ関数は偶関数)

\[P(\omega)=\frac{2\pi}{T}\sum_{k=-\infty}^{\infty}\delta(k\omega_s-\omega)=\frac{2\pi}{T}\sum_{k=-\infty}^{\infty}\delta(\omega-k\omega_s)\]

ただし，$\omega_s=\frac{2\pi}{T}$

2.サンプル値信号のフーリエ変換：

\[X_p(\omega)=\mathcal{F}[x_p(t)]=\frac{1}{2\pi}[X(\omega)*P(\omega)]\]

$[X(\omega)*P(\omega)]$：畳み込み

\[\begin{equation} \begin{aligned} X_p(\omega)&=\frac{1}{2\pi}\int_{-\infty}^{\infty}X(\tau)P(\omega-\tau)d\tau\\ &=\frac{1}{2\pi}\int_{-\infty}^{\infty}X(\tau)\frac{2\pi}{T}\sum_{k=-\infty}^{\infty}\delta(\omega-\tau-k\omega_s)d\tau\\ &=\frac{1}{T}\sum_{k=-\infty}^{\infty}\int_{-\infty}^{\infty}X(\tau)\delta(\omega-k\omega_s-\tau)d\tau \end{aligned} \end{equation}\]

$\tau=\omega-\omega_s$ のとき，デルタ関数が 1 である．よって，

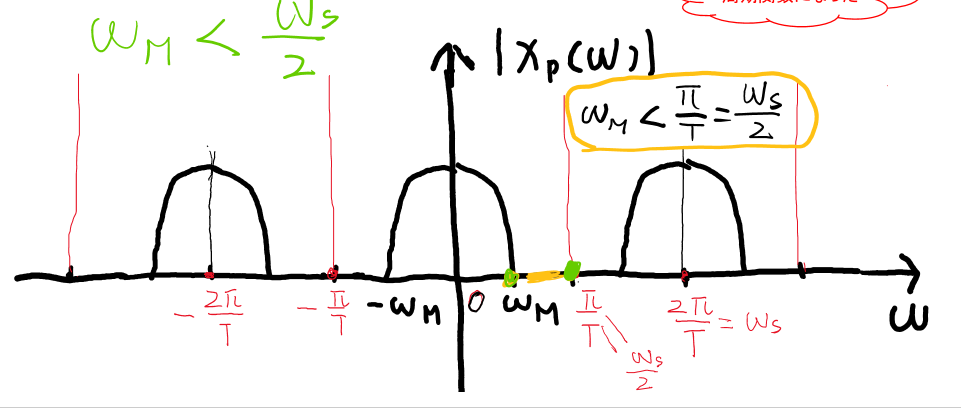
\[X_p(\omega)=\frac{1}{t}\sum_{k=-\infty}^{\infty}X(\omega-k\omega_s)\]

ただし，$\omega_s=2\pi/T$（サンプリング角周波数） (サンプルされた関数のフーリエ変換は，周期関数になった)

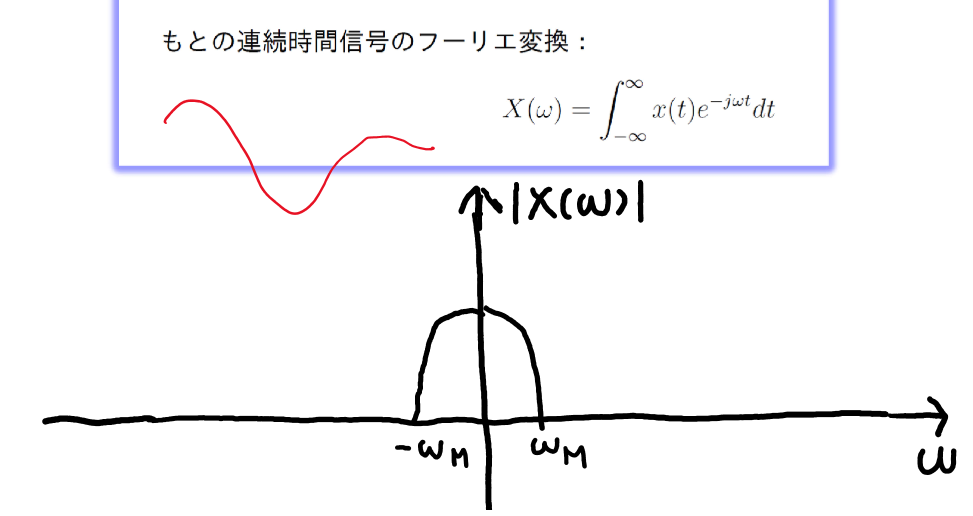
周波数領域で信号を観察する．横軸が周波数，縦軸が振幅． $|X(\omega)|^2=信号のエネルギー$ 各周波数の成分の信号の強さがわかる．

フーリエ変換の畳み込み積分の性質

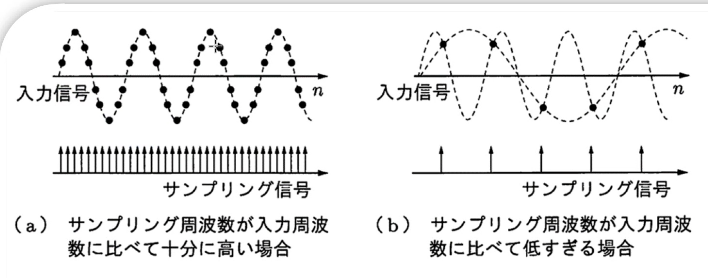
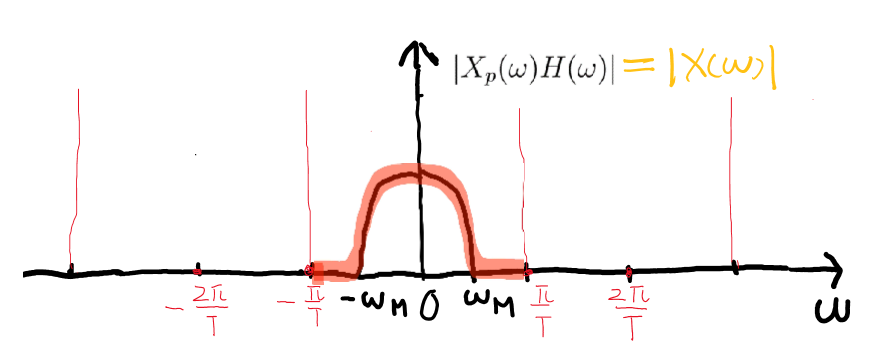
サンプリング定理

信号の最大周波数成分 $\omega_M<\omega_s/2$ のとき，$x(t)$ は $x(nt)$ から完全に回復できる．

• $\omega_M:$ 信号成分の最大角周波数

  周期関数がお互いに干渉にないことを確保する．サンプリング定理の条件を満たさない場合，周期関数がお互いに干渉，その干渉をエイリアシングという.

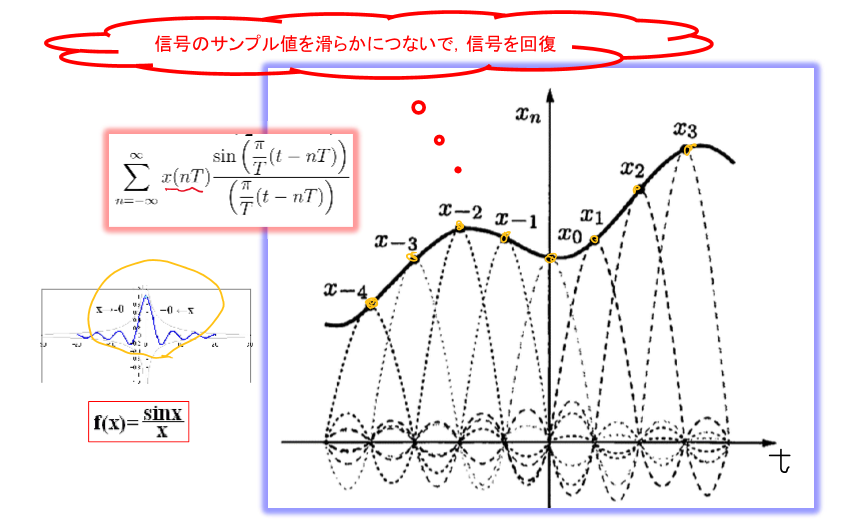
3.信号の回復（補間）

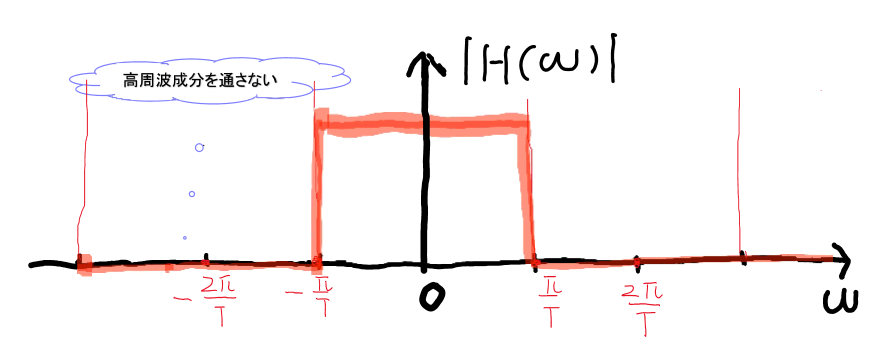
• ゲート関数 \(H(\omega)=\begin{cases} T&|\omega|\le\frac{\omega_s}{2}\\0&otherwise \end{cases}\)

逆フーリエ変換すると，

\[h(t)=\frac{\sin{(\frac{\omega_s}{2}t)}}{(\frac{\omega_s}{2}t)}\]

ただし，$\omega_s/2=\pi/T$

\[X(\omega)=X_P(\omega)H(\omega)\]

回復の公式：(フーリエ変換の畳み込み積分で回復)

\[\begin{equation} \begin{aligned} x(t)&=\int_{-\infty}^{\infty}x_p(\tau)h(t-\tau)d\tau\\ &=\int_{-\infty}^{\infty}\left[\sum_{n=-\infty}^{\infty}x(nT)\delta(\tau-nT)\right] h(t-\tau)d\tau\\ &=\sum_{n=-\infty}^{\infty}x(nT)h(t-nT)\\ &=\sum_{n=-\infty}^{\infty}x(nT)\frac{\sin{(\frac{\omega_s}{2}(t-nT))}}{(\frac{\omega_s}{2}(t-nT))}\\ &=\sum_{n=-\infty}^{\infty}x(nT)\frac{\sin{(\frac{\pi}{T}(t-nT))}}{(\frac{\pi}{T}(t-nT))} \end{aligned} \end{equation}\]

2.2 z 変換

2.2.1 離散時間信号

離散時間信号

\[x(n)=\sum_{k=-\infty}^{\infty}x(k)\delta(n-k)\]

(離散インパルス信号で表す)

離散インパルス信号

\[\delta(n)= \begin{cases} 1 &(n=0)\\ 0 &(n\neq0) \end{cases}\]

離散ステップ信号

\[u(n)=\sum_{k=0}^{\infty}\delta(n-k)=\begin{cases}1&n\ge0 \\0&n<0\end{cases}\]

離散ステップ信号と離散インパルス信号の関係

\[\delta(n)=u(n)-u(n-1)\]

2.2.2 z 変換

離散時間信号に対して，ラプラス変換すると，$z=e^{sT}$

片側 z 変換

\[X(z)=\sum_{n=0}^{\infty}x(n)z^{-n}\]

ただし，$z=e^{(\sigma+j\omega) T}=e^{sT}$

収束条件

\[|X(z)|\le\sum_{n=0}^{\infty}|x(n)|r^{-n}\]

$z=re^{j\omega T}$，

\[r^{-n}=\frac{1}{r^n}:\]

• $r>1:$ \(\lim_{n \to \infty}r^{-n}\to 0\)
• $r<1$と，\(\lim_{n \to \infty}r^{-n}\to\infty\)

逆 z 変換

\[x(n)=\frac{1}{2\pi j}\int_{C}X(z)z^{n-1}dz\]

周回積分路 $C$ は $z$ の収束領域内に取る.（あまり使わない）

• 線形性
• 時間推移
• 畳み込み和

2.3 線形定係数差分方程式による時間システムの表現

2.3.1 差分方程式

\[y(n)+\sum_{k=1}^{N}a_ky(n-k)=\sum_{k=0}^{M}b_ku(n-k)\]

2.3.2 宿題 2023-04-27-Simulation of linear discrete-time system models

2.4 離散時間モデルの伝達関数

差分方程式の z 変換

\[Y(z)+\sum_{k=1}^{N}a_kY(z)z^{-k}=\sum_{k=0}^{M}b_kU(z)z^{-k}\]

伝達関数モデル表現

\[H(z)=\frac{Y(z)}{U(z)}=\frac{\sum_{k=0}^{M}b_kz^{-k}}{1+\sum_{k=1}^{N}a_kz^{-k}}=\frac{B(z^{-1})}{A(z^{-1})}\]

インパルス応答(畳み込み表現)

\[y(n)=\sum_{k=0}^{n}u(k)h(n-k)=\sum_{k=0}^{n}u(n-k)h(k)\approx\sum_{k=0}^{N}u(n-k)h(k)\]

安定なシステムなら，時間が十分たつと，$h(k)$が減衰することに注意.$h(k)\approx0,k>N$

インパルス応答の z 変換は，離散時間システムの伝達関数．

2.5 離散時間モデルの安定性と周波数応答

2.5.1 離散時間モデルの安定性

伝達関数 $H(z)$ の極が半径 1 の円(単位円) にあれば，円周上にある単根は安定限界，単位円の外にあれば不安定．

\[\frac{1}{1-\alpha z^{-1}}:|\alpha|<1\]

2.5.2 離散時間モデルの周波数応答

$H(z)$ について，

\[z\to j\omega \implies z^{j\omega T}\]

を代入する．ただし，$\omega\in[0,\pi/T)$

離散時間システム周波数特性：

2.6 連続時間モデルから離散時間モデルの導出

2.6.1 インパルス不変の方法

\[H(z)=\sum_{n=0}^{\infty}g(n)z^{-n}\]

2.6.2 微分方程式の近似

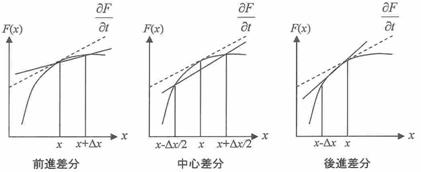
前進差分（前進矩形微分）

\[s=\frac{z-1}{T}, \quad s^{-1}=\frac{T}{z-1}\] \[sf(n)=\frac{f(n+1)-f(n)}{T},\quad s^{-1}f(n+1)=s^{-1}f(n)+Tf(n)\]

後退差分（後退矩形微）

\[s=\frac{1-z^{-1}}{T}, \quad s^{-1}=\frac{T}{1-z^{-1}}\] \[sf(n)=\frac{f(n)-f(n-1)}{T},\quad s^{-1}f(n)=s^{-1}f(n-1)+Tf(n)\]

双 1 次変換法（台形積分）

\[s=\frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}}, \quad s^{-1}=\frac{T}{2}\frac{1+z^{-1}}{1+z^{-1}}\] \[\frac{sf(n)+sf(n-1)}{2}=\frac{f(n)-f(n-1)}{T},\quad s^{-1}f(n)=s^{-1}f(n-1)+\frac{T}{2}[f(n)+f(n-1)]\]

2.6.3 宿題 1

2.6.4 宿題 2 PID 制御器のシミュレーション

2.7 フーリエ級数，フーリエ変換と z 変換の関係

2.7.1 フーリエ級数

周期関数の周期信号を扱う．複数の三角関数で信号関数を表す．

ベクトルの内積の視線から見ると，ベクトルを二つ基底ベクトルの線形結合で表される．よって，ある関数を正弦波と余弦波の線形結合で表される．

\[x(t)=x(t+T),\;f_0=\frac{1}{P},\;\omega_0=\frac{2\pi}{P}\]

フーリエ級数：

\[x(t)=\frac{a_0}{2}+\sum_{n=1}^{\infty}\left( a_n\cos{n\omega_0t}+b_n\sin{n\omega_0t}\right)\]

関数の内積： $a_n$ は余弦波成分の係数である．関数と余弦関数の内積で求める． $b_n$ は正弦波成分の係数である．関数と正弦関数の内積で求める．

\[a_n=\frac{2}{P}\int_{0}^{P}x(t)\cos{n\omega_0t}\;dt,\quad b_n=\frac{2}{P}\int_{0}^{P}x(t)\sin{n\omega_0t}\;dt\]

直交性：(関数の内積の特性：自分自身の写像が 1)

\[\frac{2}{P}\int_{0}^{P}\cos{m\omega_0t}\cos{n\omega_0t}\;dt=\delta_{mn}\] \[\frac{2}{P}\int_{0}^{P}\sin{m\omega_0t}\sin{n\omega_0t}\;dt=\delta_{mn}\] \[\frac{2}{P}\int_{0}^{P}\sin{m\omega_0t}\cos{n\omega_0t}\;dt=0\]

クロネッカのデルタ：

\[\delta_{mn}=\begin{cases}1\quad m=n\\0\quad m\ne n\end{cases}\]

パーセバルの等式：

\[\frac{2}{P}\int_{0}^{P}x^2(t)dt=\frac{a_0^2}{2}+\sum_{n=1}^{\infty}(a_n^2+b_n^2)\]

信号の平均パワー

複素数表現：

\[e^{j\omega_0t}=\cos{\omega_0t}+\sin{\omega_0t}\]

オイラーの公式により，

\[\cos{\omega_0t}=\frac{e^{j\omega_0t}+e^{-j\omega_0t}}{2},\quad \sin{\omega_0t}=\frac{e^{j\omega_0t}-e^{-j\omega_0t}}{2j}\] \[\begin{equation} \begin{aligned} a_n\cos{n\omega_0t}+b_n\sin{n\omega_0t}&=a_n\frac{e^{jn\omega_0t}+e^{-jn\omega_0t}}{2}+b_n\frac{e^{jn\omega_0t}-e^{-jn\omega_0t}}{2j}\\&=\frac{a_n-jb_n}{2}e^{jn\omega_0t}+ \frac{a_n+jb_n}{2}e^{-jn\omega_0t} \end{aligned} \end{equation}\] \[c_n=\frac{a_n-jb_n}{2}\]

複素数フーリエ：

\[x(t)=\sum_{n=-\infty}^{\infty}c_ne^{j\omega_0t}\] \[c_n=\frac{1}{P}\int_{0}^{P}x(t)e^{-jn\omega_0t}dt\]

• 複素数の内積 \(\frac{1}{P}\int_{0}^{P}e^{jm\omega_0t}e^{-jn\omega_0t}dt=\delta_{mn}\)

パーセバルの等式]]

\[\frac{2}{P}\int_{0}^{P}x^2(t)dt=\sum_{n=-\infty}^{\infty}|c_n|^2\]

2.7.2 連続時間フーリエ変換

独立波を扱うとき，$p\to\infty$

独立波を周期無限大の周期関数として扱い，フーリエ級数を行うと，フーリエ変換である．時間領域から周波数領域へ変換できる．

\[X(\omega)=\int_{-\infty}^{\infty}x(t)e^{-j\omega t}dt\] \[x(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}X(\omega)e^{j\omega t}dt\]

フーリエ変換が発散するとき($X(\omega)=\infty$)，ラプラス変換を導入する．$j\omega$を$s=\sigma+j\omega$で置き換えると取り扱う．($\sigma>0$)

2.7.3 離散フーリエ変換#5.1 離散時間フーリエ変換の導出|離散時間フーリエ変換

時間だけを離散化する．

2.7.4 離散フーリエ変換

時間と周波数を離散化する