Post

ベイズ推定(Bayesian inference)

Posted
Preview Image
By Guang-Ze Yang 16 min read

Homepage: https://youkoutaku.github.io/

1.問題

観測データが ($x_1$, $y_1$), … , ($x_M$, $y_M$) が得られたとき，この観測結果を直線 $y=\theta_0+\theta_1 x$ に回帰したい．回帰直線のパラメータ $\theta_0$ と $\theta_1$ を逐次ベイズ学習により推定し，その結果を考 察しなさい．

手順１：観測データの生成

  1. $x_1$ から $x_M$ を一様乱数により生成する．
  2. $y_1$ から $y_M$ を の計算式に従って生成する．ここで， $𝜃_0$ と $𝜃_1$ は適当な値を与える．また $𝜀_j$ は平均が 0 で分散が $𝜎^2$ の正規乱数とする．

手順２：逐次ベイズ学習による $\theta_0$ と $\theta_1$ の推定

  1. 事前分布のパラメタを設定する
  2. ($x_j$, $y_j$)が得られる毎に更新式にしたがい，パラメタ更新を行う．𝛼 と 𝛽 は各自で決める．ただし，ノイズの標準偏差が𝜎のとき，
\[𝛽=(\frac1\sigma)^2\]

で与えられることに注意する．

考察のポイント

  • 𝛼 と 𝛽 の影響
  • 雑音レベルの影響（S/N）

2.ベイズ線形回帰

2.1 観測モデル

\[y=\theta_0+\theta_1\phi_1(x)+\dots+\theta_N\phi_N(x) + ϵ\]

⇒

\[\boldsymbol y=\boldsymbol H \boldsymbol \theta + \boldsymbol ϵ\]

ただし，

\[y=\begin{bmatrix}y_1\\y_2\\\vdots\\y_M\end{bmatrix}\quad x=\begin{bmatrix}x_1\\x_2\\\vdots\\x_M\end{bmatrix} \boldsymbol{\theta}=\begin{bmatrix}\theta_0\\\theta_1\\\vdots\\\theta_N \end{bmatrix}\boldsymbol{ϵ}=\begin{bmatrix}ϵ_0\\ϵ_1\\\vdots\\ϵ_N \end{bmatrix}\] \[H=\begin{bmatrix}1&\phi_1(x_1)&\cdots&\phi_N(x_1)\\1&\phi_1(x_2)&\cdots&\phi_N(x_2)\\\vdots&\vdots&\vdots&\vdots\\1&\phi_1(x_M)&\cdots&\phi_N(x_M)\end{bmatrix}\]

2.2 正規分布の仮定

  • 事前分布(事前データ):
\[f(\boldsymbol\theta)=N(\boldsymbol\theta|\boldsymbol\mu,\boldsymbol v^{-1})\]
  • 尤度(観測分布，観測データ)
\[f(\boldsymbol y|\boldsymbol\theta)=N(\boldsymbol y|\boldsymbol H \boldsymbol\theta, \boldsymbol\Lambda^{-1})\]

ただし，

\[\boldsymbol{\Lambda}=\beta\boldsymbol{I}\\\boldsymbol{\mu}=\boldsymbol{0}\\\boldsymbol{v}=\alpha\boldsymbol{I}\]

ここで，事前分布の分散行列が $\boldsymbol{v}^{-1}$であるため，$\alpha$ が小さいほど，事前分布のバラツキが大きくなる．観測分布の分散行列が $\boldsymbol{Λ}^{-1}$であるため，$\beta$ が小さいほど，観測分布のバラツキが大きくなる．

  • ノイズ
\[\boldsymbol ϵ=N(\boldsymbol 0,\sigma^2\boldsymbol I)\] \[\text{gzai}:\frac{\alpha}{\beta}\] \[S/N: 観測値 \boldsymbol y の標準偏差/ノイズ \boldsymbol ϵ の標準偏差\]

2.3 推定解

  • 事後分布
\[f(\boldsymbol\theta|\boldsymbol y) = N(\boldsymbol\theta|\boldsymbol{\overline{\theta}},\boldsymbol Γ^{-1})\]
  • 精度行列
\[\boldsymbol Γ=\alpha \boldsymbol I + \beta \boldsymbol H^T \boldsymbol H\]
  • MMSE推定解
\[\boldsymbol{\overline{\theta}} = \boldsymbol Γ^{-1} \beta \boldsymbol H^T \boldsymbol y\]

3.プログラム

3.1 ライブラリのインポート

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# 以下のライブラリを使うので、あらかじめ読み込んでおいてください
import numpy as np
import scipy as sp
import pandas as pd
from pandas import Series, DataFrame
from scipy.stats import multivariate_normal

# 可視化ライブラリ
import matplotlib.pyplot as plt
import matplotlib as mpl
import matplotlib.mlab as mlab
import seaborn as sns
%matplotlib inline

# 小数第3位まで表示
%precision 3

1

'%.3f'

1
2
3
4
5
6
7
8
9
10

#観測データと回帰直線の描画関数
def plot_data(ax,x_min, x_max, x, y, x_seq):
    ax.set_xlim(x_min, x_max), ax.set_ylim(x_min, x_max)
    ax.scatter(x, y, color = 'b')
    ax.plot(x_seq, mu[0]+mu[1]*x_seq, color='r')

#事後分布の表示関数（ヒートマップ）
def plot_heatmap(ax, x_min, x_max, rv, x_seq, y_seq, pos):
    ax.set_xlim(x_min, x_max), ax.set_ylim(x_min, x_max)
    ax.pcolor(x_seq, y_seq, rv.pdf(pos), cmap=plt.cm.jet)

3.2 観測データの生成

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

#シミュレーション条件
np.random.seed(0);               #ランダムシードの固定
c = np.array([-0.3, 0.5]);       #パラメータの真値 theta

sigma = 0.2;                     #ノイズの標準偏差
alpha =0.1;                      #事前分布の精度パラメタ

beta = 1.0 / (sigma ** 2);       #ノイズの精度パラメタ
gzai = alpha/beta;               #正則化定数
mu = np.zeros(2);                #事前分布の平均値ベクトル mu
Ganma = alpha * np.identity(2);  #事前分布の精度行列
inv_Ganma=np.linalg.inv(Ganma);  #事前分布の共分散行列
M = 50;                          #サンプル数

# 描画設定
x_min, x_max = -1.0, 1.0         #xの描画範囲
y_min, y_max = -1.0, 1.0         #yの描画範囲

# ノイズ
# np.random.normal(平均、標準偏差、サンプル数)
e= np.random.normal(0, sigma, M)

#観測データxの生成:np.random.uniform(a, b, サンプル数) aからｂまでの一様乱数
x=np.random.uniform(x_min, x_max, M)

#観測データyの生成
y=c[0]+c[1]*x+e

3.3 逐次ベイズ学習

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

# 描画設定
fig = plt.figure(figsize = (10, 6 * M))
x_seq, y_seq = np.mgrid[x_min:x_max:.01, y_min:y_max:.01]  #メッシュグリッドの作成
pos = np.empty(x_seq.shape + (2,))
pos[:, :, 0] = x_seq; pos[:, :, 1] = y_seq
rv = multivariate_normal(mu,inv_Ganma)  #2次元正規分布の設定
axes = [fig.add_subplot(M + 1, 2, k) for k in range(1, 3)]
plot_heatmap(axes[1], x_min, x_max, rv, x_seq, y_seq, pos)

# 逐次ベイズ学習
result = []
for j in range(M):

    H = np.array([1.0, x[j]])

    # estimate parameters
    pre_Ganma = Ganma
    Ganma = pre_Ganma + beta * H.reshape(2, 1) * H
    inv_Ganma = np.linalg.inv(Ganma)
    mu = inv_Ganma.dot(pre_Ganma.dot(mu) + beta *  H * y[j])

    # plot
    rv = multivariate_normal(mu,inv_Ganma)  #2次元正規分布の設定
    axes = [fig.add_subplot(M + 1, 2, (j + 1) * 2 + k) for k in range(1, 3)]
    plot_data(axes[0], x_min, x_max, x[:j+1], y[:j+1], x_seq)
    plot_heatmap(axes[1], x_min, x_max, rv, x_seq, y_seq, pos)
    result.append([j, mu[0], mu[1], c[0], c[1]])

plt.show()

png

1
2
3

#推定値確認
df = DataFrame(data=result, columns = ['j','mu[0]','mu[1]','c[0]','c[1]'])
df
jmu[0]mu[1]c[0]c[1]
00-0.1961740.133802-0.30.5
110.6891391.559455-0.30.5
22-0.0919030.495938-0.30.5
33-0.0672000.422107-0.30.5
44-0.0546820.409682-0.30.5
55-0.1786640.307591-0.30.5
66-0.1229250.401981-0.30.5
77-0.1372100.461177-0.30.5
88-0.1662600.414366-0.30.5
99-0.1728690.432366-0.30.5
1010-0.1774690.424336-0.30.5
1111-0.1631380.428268-0.30.5
1212-0.1553630.442815-0.30.5
1313-0.1634470.437846-0.30.5
1414-0.1646980.436398-0.30.5
1515-0.1713190.451264-0.30.5
1616-0.1632910.444574-0.30.5
1717-0.1729270.462257-0.30.5
1818-0.1767180.464833-0.30.5
1919-0.1884280.487693-0.30.5
2020-0.2157110.500593-0.30.5
2121-0.2135680.500739-0.30.5
2222-0.2112750.494130-0.30.5
2323-0.2241710.478620-0.30.5
2424-0.2063890.492221-0.30.5
2525-0.2190110.503851-0.30.5
2626-0.2220300.501989-0.30.5
2727-0.2245710.509199-0.30.5
2828-0.2149850.517580-0.30.5
2929-0.2054990.536104-0.30.5
3030-0.2069710.537011-0.30.5
3131-0.2081060.535684-0.30.5
3232-0.2133880.547829-0.30.5
3333-0.2320950.522497-0.30.5
3434-0.2352940.525330-0.30.5
3535-0.2356600.525998-0.30.5
3636-0.2300490.530969-0.30.5
3737-0.2270550.518751-0.30.5
3838-0.2328760.508740-0.30.5
3939-0.2345850.515564-0.30.5
4040-0.2432080.505223-0.30.5
4141-0.2500830.511826-0.30.5
4242-0.2620910.494843-0.30.5
4343-0.2506720.518613-0.30.5
4444-0.2533640.521745-0.30.5
4545-0.2567040.519256-0.30.5
4646-0.2638070.513454-0.30.5
4747-0.2611130.515408-0.30.5
4848-0.2671020.524312-0.30.5
4949-0.2697060.518660-0.30.5
1
2
3
4
5
6
7
8
9
10
11

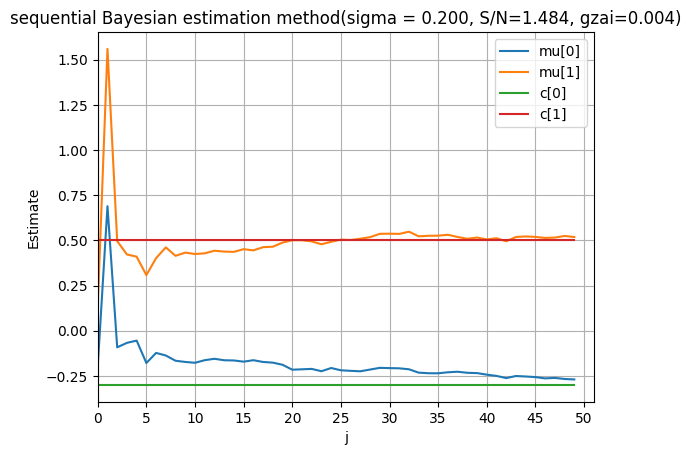
#推定値描画
# plot
df.plot(x='j', y=['mu[0]','mu[1]','c[0]','c[1]'] )
plt.title('sequential Bayesian estimation method(sigma = %.3f, S/N=%.3f, gzai=%.3f)'%(sigma, np.std(c[0]+c[1]*x)/sigma, gzai ))
plt.xlabel('j')
plt.ylabel('Estimate')
plt.xticks(np.arange(0, M+1, M/10)) #メモリの値を設定
plt.xlim(0,M+1)
plt.grid(True)
plt.show()

png

4. 考察

4.1 $\beta$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

#シミュレーション条件
np.random.seed(0);               #ランダムシードの固定
c = np.array([-0.3, 0.5]);       #パラメータの真値 theta

sigma = 0.8;                     #ノイズの標準偏差
alpha =0.1;                      #事前分布の精度パラメタ

beta = 1.0 / (sigma ** 2);       #ノイズの精度パラメタ
gzai = alpha/beta;               #正則化定数
mu = np.zeros(2);                #事前分布の平均値ベクトル mu
Ganma = alpha * np.identity(2);  #事前分布の精度行列
inv_Ganma=np.linalg.inv(Ganma);  #事前分布の共分散行列
M = 50;                          #サンプル数

# 描画設定
x_min, x_max = -1.0, 1.0         #xの描画範囲
y_min, y_max = -1.0, 1.0         #yの描画範囲

# ノイズ
# np.random.normal(平均、標準偏差、サンプル数)
e= np.random.normal(0, sigma, M)

#観測データxの生成:np.random.uniform(a, b, サンプル数) aからｂまでの一様乱数
x=np.random.uniform(x_min, x_max, M)

#観測データyの生成
y=c[0]+c[1]*x+e

# 逐次ベイズ学習
result = []
for j in range(M):

    H = np.array([1.0, x[j]])

    # estimate parameters
    pre_Ganma = Ganma
    Ganma = pre_Ganma + beta * H.reshape(2, 1) * H
    inv_Ganma = np.linalg.inv(Ganma)
    mu = inv_Ganma.dot(pre_Ganma.dot(mu) + beta *  H * y[j])
    # plot
    rv = multivariate_normal(mu,inv_Ganma)  #2次元正規分布の設定
    axes = [fig.add_subplot(M + 1, 2, (j + 1) * 2 + k) for k in range(1, 3)]
    plot_data(axes[0], x_min, x_max, x[:j+1], y[:j+1], x_seq)
    plot_heatmap(axes[1], x_min, x_max, rv, x_seq, y_seq, pos)
    result.append([j, mu[0], mu[1], c[0], c[1]])

#推定値確認
df = DataFrame(data=result, columns = ['j','mu[0]','mu[1]','c[0]','c[1]'])
#推定値描画
# plot
df.plot(x='j', y=['mu[0]','mu[1]','c[0]','c[1]'] )
plt.title('sequential Bayesian estimation method(sigma = %.3f, S/N=%.3f, gzai=%.3f)'%(sigma, np.std(c[0]+c[1]*x)/sigma, gzai ))
plt.xlabel('j')
plt.ylabel('Estimate')
plt.xticks(np.arange(0, M+1, M/10)) #メモリの値を設定
plt.xlim(0,M+1)
plt.grid(True)
plt.show()

png

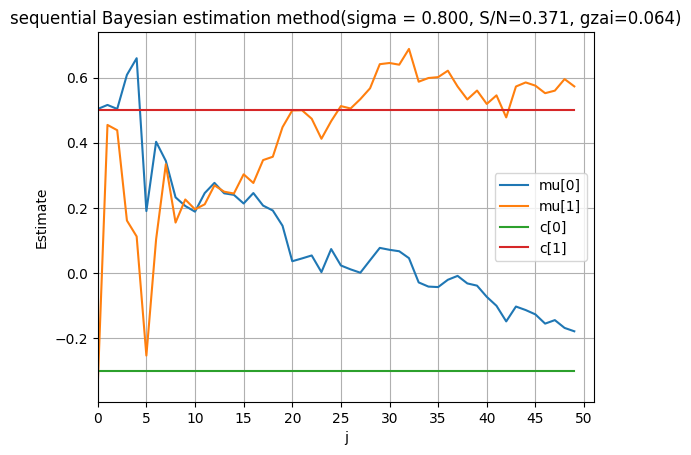
ここで，ノイズの標準偏差を大きくして $\sigma=0.8$ とおく．

\[\beta=\frac1\sigma^2\]

$\beta$ が小さくなることがわかる．

上の描画結果が示すように，ノイズの標準偏差 $\sigma$ を大きく，$\beta$ が小さく，推定性能が悪くなることがわかる．それで，$\beta$ が小さくするとノイズのバラツキが大きくなり，観測分布の偏差行列 $Λ^{-1}$ が大きくなるため，推定の性質が悪くなることは一般的に考えられる．予想通りである．

4.2 $\alpha$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

#シミュレーション条件
np.random.seed(0);               #ランダムシードの固定
c = np.array([-0.3, 0.5]);       #パラメータの真値 theta

sigma = 0.2;                     #ノイズの標準偏差
alpha =0.8;                      #事前分布の精度パラメタ

beta = 1.0 / (sigma ** 2);       #ノイズの精度パラメタ
gzai = alpha/beta;               #正則化定数
mu = np.zeros(2);                #事前分布の平均値ベクトル mu
Ganma = alpha * np.identity(2);  #事前分布の精度行列
inv_Ganma=np.linalg.inv(Ganma);  #事前分布の共分散行列
M = 50;                          #サンプル数

# 描画設定
x_min, x_max = -1.0, 1.0         #xの描画範囲
y_min, y_max = -1.0, 1.0         #yの描画範囲

# ノイズ
# np.random.normal(平均、標準偏差、サンプル数)
e= np.random.normal(0, sigma, M)

#観測データxの生成:np.random.uniform(a, b, サンプル数) aからｂまでの一様乱数
x=np.random.uniform(x_min, x_max, M)

#観測データyの生成
y=c[0]+c[1]*x+e

# 逐次ベイズ学習
result = []
for j in range(M):

    H = np.array([1.0, x[j]])

    # estimate parameters
    pre_Ganma = Ganma
    Ganma = pre_Ganma + beta * H.reshape(2, 1) * H
    inv_Ganma = np.linalg.inv(Ganma)
    mu = inv_Ganma.dot(pre_Ganma.dot(mu) + beta *  H * y[j])
    # plot
    rv = multivariate_normal(mu,inv_Ganma)  #2次元正規分布の設定
    axes = [fig.add_subplot(M + 1, 2, (j + 1) * 2 + k) for k in range(1, 3)]
    plot_data(axes[0], x_min, x_max, x[:j+1], y[:j+1], x_seq)
    plot_heatmap(axes[1], x_min, x_max, rv, x_seq, y_seq, pos)
    result.append([j, mu[0], mu[1], c[0], c[1]])

#推定値確認
df = DataFrame(data=result, columns = ['j','mu[0]','mu[1]','c[0]','c[1]'])
#推定値描画
# plot
df.plot(x='j', y=['mu[0]','mu[1]','c[0]','c[1]'] )
plt.title('sequential Bayesian estimation method(sigma = %.3f, S/N=%.3f, gzai=%.3f)'%(sigma, np.std(c[0]+c[1]*x)/sigma, gzai ))
plt.xlabel('j')
plt.ylabel('Estimate')
plt.xticks(np.arange(0, M+1, M/10)) #メモリの値を設定
plt.xlim(0,M+1)
plt.grid(True)
plt.show()

png

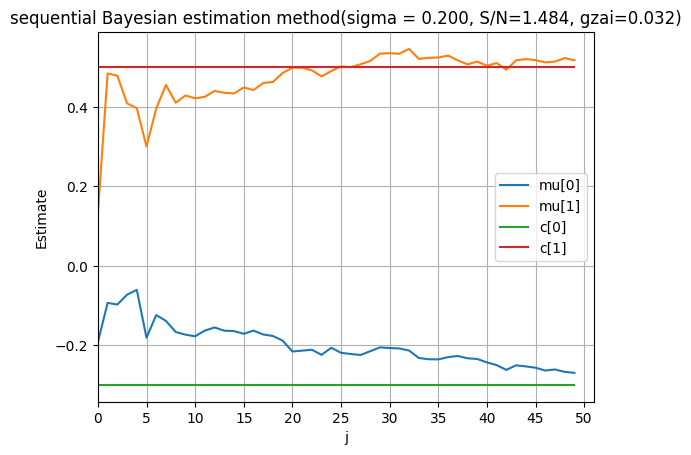
ここで，$\alpha=0.8$ が大きくすると，事前分布の偏差行列 $v^{-1}$ が小さくなることがわかる．

上の描画結果が示すように，$\alpha=0.8$ が大きく，事前分布の偏差行列が小さく，推定性能が良くなることがわかる．それで，$\alpha=0.8$ が大きくすると事前分布のバラツキが小さい．すなわち，事前情報が正しさが高い．したがって，推定の性質が良いことだと考えられる．予想通りである．

4.3 S/N

2.2で述べたように,\(S/N:観測値 \boldsymbol y の標準偏差/ノイズ \boldsymbol ϵ の標準偏差\)

したがって，$S/N$ が大きいほど，観測分布の標準偏差がノイズの標準偏差より大きい．$S/N$ が小さいほど，観測分布の標準偏差がノイズの標準偏差より小さい．

上記の結果から見ると，$S/N$ が大きいほど，推定性能がよいことがわかる．解析の予想通りである．

Math, Probability Theory
Probability Linear regression Bayesian inference JP
This post is licensed under CC BY 4.0 by the author.